1. INTRODUCTION
The production of lunar soil simulants is essential in preparation for future lunar missions aiming to utilize lunar resources, rover operations, and soil excavation (Gaier 2008). However, preparing experiments for lunar exploration in the very different environment of the Moon compared to the Earth requires considerable effort.
The first lunar regolith simulants were developed in preparation for the Apollo program to simulate lunar surface environments (Sibille et al. 2006). However, it was later revealed that the lunar simulants used in the Apollo program differed from the actual lunar soil environment and caused problems. Issues arose due to the presence of fine, sharp dust particles in the lunar soil (Gaier 2005).
With the end of the Apollo program the returned samples of lunar regolith made it possible to study the physical and chemical composition of the lunar surface is unprecedented detail (Taylor et al. 2001, 2010). From this, the need for accurate lunar simulants became apparent. Thus, the development of more accurate lunar simulants began. As various countries and companies attempted lunar exploration, a variety of lunar simulants were developed (McKay et al. 1994; Ryu et al. 2015). Conducting experiments to simulate the lunar environments using these simulants has contributed significantly to the progress of lunar exploration such as preparation for lunar resource extraction, rover maneuver (Allan et al. 2019; Shi et al. 2022; Wang et al. 2022). However, current lunar simulants have also been criticized for their many limitations that these simulants are representing bulk average of mare or highland rather than specifically represent certain interesting terrain spots (Taylor et al. 2016).
In the past, the trend in lunar exploration has been to perform in-situ measurements and to obtain lunar samples to the Earth. This relatively did not require complex identification of interactions between the lunar regolith and mission operations compared to missions currently being envisioned. Hence lunar regolith simulants to support lunar explorations were tend to be bulk and did not need to be specific. Resulting in building a simulant based on the mare or highland dichotomy.
However, as the trend of modern lunar exploration missions has shifted, it has become important to prepare for in-situ resource utilization (ISRU) of space resources. In the field of lunar resource exploration and utilization, a high degree of chemical and mineralogical similarity is required (Ryu et al. 2015). To effectively adapt to the new trends in lunar exploration, it is essential to meet these requirements.
In future exploration missions for supporting space resource exploration and utilization, more advanced simulants that reflect the subtle differences between terrains with a higher accuracy are required. To achieve this, it is necessary to move away from the conventional approach of developing a single simulant with bulk compositions. Instead, we need to rapidly develop simulants with precise chemical compositions to correspond to various, specific terrains. In other words, rather than developing one simulant with a single bulk composition, simulants for multiple terrains need to be developed as a series approach. However, the current methodology for a simulant development takes too long to develop series simulant. To address this, we have constructed a simulant development framework equipped with automatic mixing ratio calculation functionality with the particle swarm optimization (PSO) algorithm (Kennedy & Eberhart, 1995). We established a database for compositions of potential target lunar terrains and that of prepared material samples. Using the target and sample databases along with automated algorithm, we aim to validate the developed framework by producing and analyzing prototype simulants using this framework.
2. METHODS
Based on available rock samples of varying composition, we aimed to automatically calculate the mixture ratios of these components to obtain any desired simulant composition. The procedure was based on the results of analysis of ten major molecules (SiO2, Al2O3, FeO, CaO, MgO, K2O, Na2O, TiO2, MnO, P2O5). In Section 2.1 we describe the PSO algorithm to find the optimal mixture ratios. Following, the database of rock samples is established and manufactured prototype simulant (see Section 2.2).
To implement the core functionality of automatic mixing ratio calculation, PSO algorithm was selected.
Calculation of ratios based on molecular proportions rather than mineral compositions should not pose a problem. Rocks that actually make up lunar soil such as basalt, anorthosite, and peridotite were used as ingredients. This calculation can be interpreted as finding points where ten-dimensional vectors converge to target composition vector closely. Since rocks of the same type as those found on the Moon are being used as materials, there should be no significant differences in mineral composition. Additionally, by combining various samples of rocks such as basalt, anorthosite, and peridotite, the proportion of the same types of rocks can be finely adjusted based on their molecular composition ratios. This approach goes beyond the traditional simulant development process by considering molecular composition, which is expected to result in even higher mineralogical accuracy.
Crucially, in the current simulant development process, fine mineral variations within rocks have not been considered. However, using rocks of the same type as the target allows for consideration of molecular proportions, resulting in better convergence of mineral compositions compared to existing simulants. If necessary, using multiple samples per each rock type can further enhance the convergence of mineral compositions.
The optimization problem of adjusting the prescribed target ratios of ten major molecules using some of the various samples is highly complex since we are seeking n of R10 vectors (where n is number of used samples), where them converging close. This causes significant risk of falling into local optimum and failing to converge to the global optimum. Therefore, a swarm-based algorithm is desired. Among them, PSO is a computational optimization algorithm inspired by the social behavior of organisms such as flocks of birds or schools of fish. In PSO, particles move through the search space, adjusting their positions based on their own experiences and the experiences of neighboring particles to find the optimal solution (Kennedy & Eberhart 1995).
The movement of each particle is influenced by two main factors: its own best-known position and the best-known position of neighboring particles. These positions are iteratively updated based on evaluations of fitness functions measuring the quality of each particle’s solution (Kennedy & Eberhart 1995). PSO is characterized by its simplicity, ease of implementation, and efficiency in searching high-dimensional spaces. It is suitable for simulant mixing ratio calculations as it does not require derivatives in the optimization process and being efficient in high dimensions. We implemented this algorithm using the pyswarm library in Python.
The code first loads the target sample material composition and the available sample material compositions from a pre-built .csv file. Then, it repeatedly performs calculations to find the mixture ratio that results in the least magnification from the target. The initial values after algorithm initialization are set randomly, the calculation results also exhibit relatively high randomness and it is sensitive to initial parameters.
These issues might cause early convergence, so we circumvented such problems by applying random initial parameters and iteratively computing until selecting the best value. Empirically, convergence typically begins to be significant around 50,000 iterations, and meaningful accuracy improvement is difficult to expect even with further computations around 100,000 iterations. Therefore, computations are performed around 100,000 iterations.
The “best value” is defined as the mixture ratio where the deviation of each component ratio from 100% is minimized when the component ratios are 100% of the target value. That is, after calculating how much percent each component value has compared to the target composition for ten molecules. For example, if the calculated ratio for a molecule matches the target ratio 50%, reaching 55% in the calculation, it is defined as 110%. Then, the mixture ratio with the lowest sum of deviations from 100% for all ten molecules is selected. If defining the error as %p, accuracy cannot be guaranteed for molecules with relatively lower composition ratios.
The mentioned database currently encompasses material compositions from Apollo mission sample X-ray fluorescence (XRF) data (Rose et al. 1972), and is currently being conducted by selecting interesting terrains. It is necessary to consider the concept of building a database that can load and process data immediately. Additionally, samples held in the laboratory are analyzed via XRF, and after being databased, when selecting the terrain to be simulated, it automatically proceeds with selecting each rock and calculating the mixture, allowing us to simply mix them based on that.
The sample database includes rock samples of Jeju basalt YS-2W, Hadong-Sancheong anorthosite 003A / 007A, Mexican Olivine, Handeok mine Non-Mag, Hadong-Sancheong ilmenite anorthosite 005, and Gongju Basin basalt GB151202-2A, Gogeumdo basalt GGD-15 (Table 1). Among these, Jeju basalt YS-2W, Hadong-Sancheong ilmenite anorthosite 005, Handeok mine Non-Mag, Mexican Olivine, and Hadong-Sancheong anorthosite 007A were used. While it should be strictly avoided in actual simulant development, for the purpose of validating how well the program converges to the target values, Al2O3, CaO, and P2O5 chemicals were also included in the material list, and the lunar simulant was produced by mixing according to the ratios provided by the program.
The target for the simulation was set to the Apollo 14 bulk soil sample, 14163 soil (Rose et al. 1972). Changing this target yields immediate recalculations, so its significance is not substantial.
Subsequently, the mixture was analyzed using XRF to compare with the target values, with multiple measurements conducted for verification.
3. RESULTS
By running the ratio calculation program, we optimized the composition to match the target 14163 soil sample using our currently available samples. The simulant is then created by mixing the samples according to the calculated ratios.
The Fig. 1 shows the mineral distribution of the simulant produced in this study. The Fig. 2 shows a photo of the lunar simulant produced in this study with the method described in the section 2.2. The name of this simulant is Kigam Lunar Simulant 6 (a.k.a. Kigam-L6).

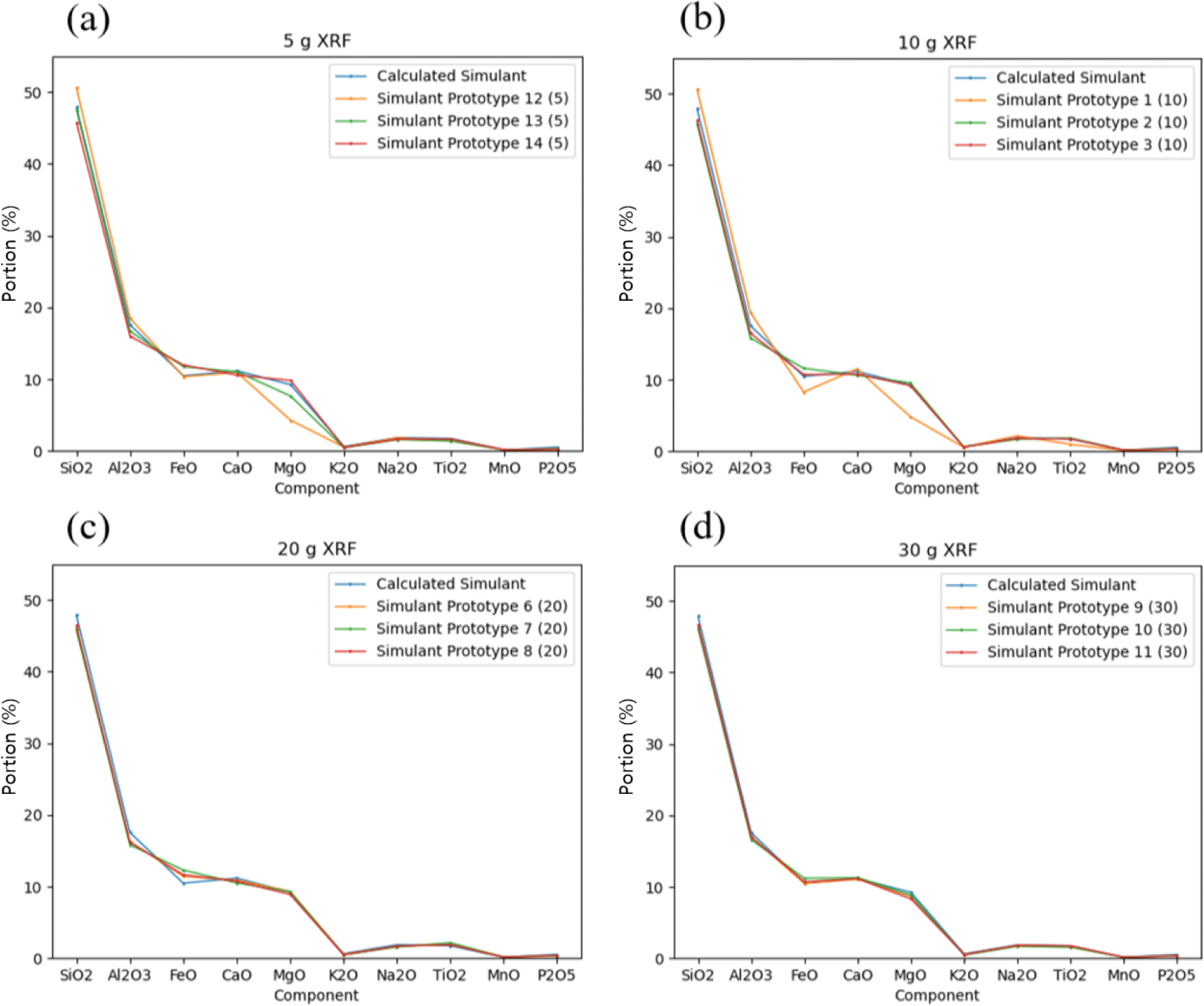
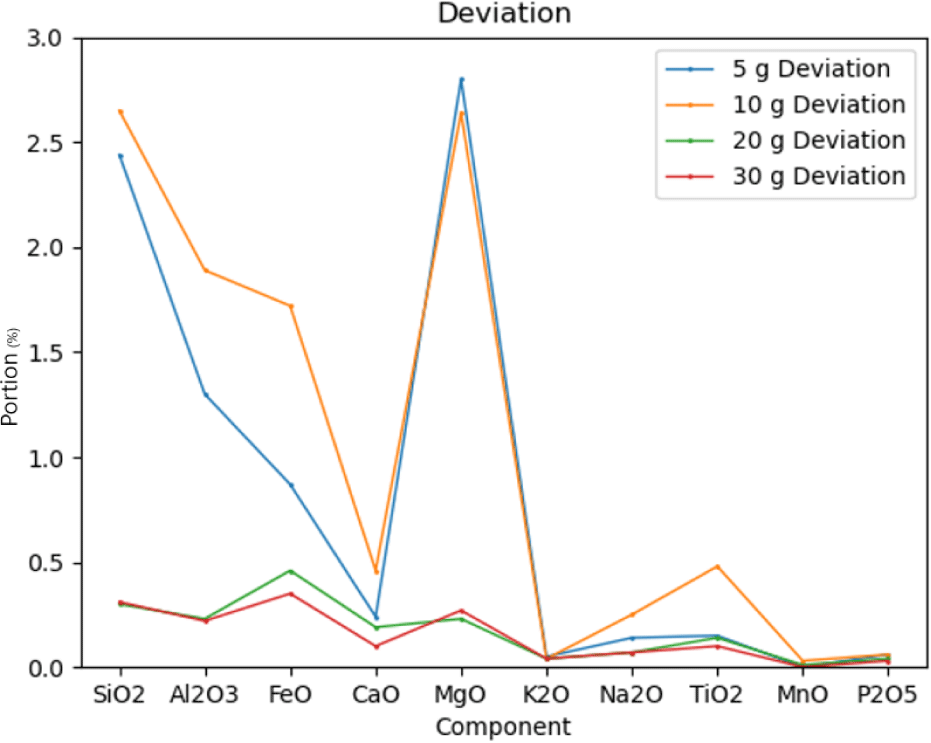
We also investigated the sampling or mixing method in generating simulant using a different amount of feed stock materials in making lunar simulants. Based on our results, the deviation significantly decreased when the same amount is over 20 g. The summary result is listed in Fig. 3(a)–(d) and Fig 4. The results demonstrate the optimal sample amount could be at least 30 g when mixing feed stock materials in making lunar simulant (Fig. 4).
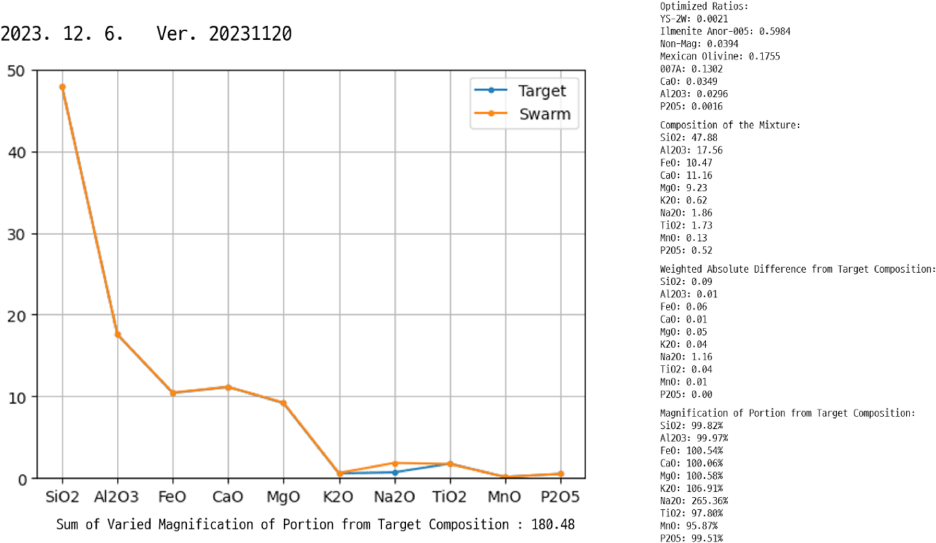
The optimal mixing ratio calculated using the automated program shows nearly perfect chemical composition in almost all aspects, except for a significant excess of Na2O content.
4. DISCUSSIONS
Table 2 is error analyses of which carried out on other simulants simulated the same 14,163 sample based on aforementioned ‘best value’ (see 2.1.). In the case of Korean Lunar Simulant-1 (KLS-1), which serves the purpose of space architecture, significant deviations in chemical composition were observed while calculated ratio through the framework showed significantly lower error from the target ratio.
KLS refers to composition of KLS-1 Simulant, PSO refers to composition calculated with PSO algorithm of developed program framework on this research.
Adapted from Ryu et al. (2015) with permission of Korean Geotechnical Society.
While KLS-1 was compared because of its identical simulation target, it was found that other simulants also exhibit considerable deviations in chemical composition. Utilizing automated calculation programs could dramatically reduce such errors.
The results are generally in line with the target. The slight deviations may be due to the heterogeneity of the prototype, as evidenced by the frequency of occurrence when increasing the weight. In addition, the manual mixing of the components can contribute to these deviations.
The discrepancy of excessive Na2O is primarily due to inherent differences in the compositions of terrestrial rocks and lunar rocks (Narendranath et al. 2022), and it highlights the need for more detailed study of the samples. It is inevitable that some samples have excessive Na content since sourcing materials from Earth makes it challenging to match precisely. Similarly, substituting FeO with Fe2O3 is inevitable.
Initially, chemicals were mixed to check that the proportions were correct, but for actual simulant development, all components must be replaced with rock samples rather than chemicals.
At present, calculations are performed only for ten major molecules (SiO2, Al2O3, Fe2O3, CaO, MgO, K2O, Na2O, TiO2, MnO, P2O5), but this is due to the analysis progress in the analysis of currently available samples, and calculation of trace elements and mineral composition ratios is also readily feasible.
Now, with just the proper samples provided, it is possible to quickly replicate the chemical composition of desired regions, with the ability to produce simulants immediately once the processing time for materials is accounted for. Of course, physical processing and other steps are necessary. Essentially, this enables rapid experimentation for resource extraction at specific landing sites and space construction, moving beyond the conventional dichotomy of highland/mare terrains.
Furthermore, there is a plan to digitize data from Apollo, Chang’e, and Luna samples entirely. However, the varied formats pose challenges, so efforts are being made to find efficient solutions.
5. CONCLUSIONS
In this research, we have tried to respond to the demand for a new method of developing regolith simulants. Our main focus was on ensuring a sophisticated reproduction of the chemical composition, to create a simulant that could transcend the mare/highland dichotomy and reflect the subtle differences of each terrain. The purpose was to develop a lunar regolith simulant that could be used for lunar resource extraction experiments that will be needed in the near future.
In order do this quickly and effectively, we attempted to automate it using the PSO algorithm, and as a result, it became possible to produce a variety of simulants at a high speed in the future if appropriate materials were used. As a result, we have been able to dramatically reduce the time consumed while developing a regolith simulant.
However, there is still much room for improvement to produce the ideal lunar regolith simulant. In the future, consideration of the physical composition of simulants will be crucial, and will require exploration of options. parameters such as particle size, particle shape, glass composition, ion distribution, submicroscopic iron and the conversion of Fe2O3 to FeO need to be considered. Automating these aspects may be challenging since these processes require innovation in the actual hardware and these issues arise from the properties of the raw materials, the host rocks. For the time being, the plan is to continue with the current methods and explore additional options for automation.









