1. INTRODUCTION
Saturn is known to have a pronounced plasma and radio wave emission system (Gurnett et al. 1981, 2005;Kurth & Gurnett 1991) like other outer planets such as Jupiter, Uranus, Neptune, and also the earth, reflecting the global view of magnetospheric dynamics. These emissions are completely characterized by non-thermal features of particle distribution in velocity space (i.e., ∂f/∂v|| > 0). Stochastic processes and instabilities generated within the magnetosphere could be considered as a response mechanism for these emissions, which are influenced by the particle species available in the magneto plasma and magnetospheric forces. Saturn consists of charged particles with versatile energy ranges and neutral from various satellites and ionospheres of giant planets and the solarfields wind. When these charged particles interact with the wave propagating within the magnetosphere, they can exchange energy and momentum and thus the wave can grow. The major contributor, Enceladus, used Saturn’s magnetic properties to fill magnetosphere of Saturn. Some unbiased species are contemplated to be ionized through accuse trade of magnetospheric plasma, sun oriented intense UV radiation and electron impact. These recently created particles move at the Kepler speed and later speed up to (nearly) the Saturn corotation velocity. The primary driver of this speed increase is E × B floats along the cycloidal direction introducing temperature anisotropy in ions participating in transportation around. The low ion frequency (i.e., f < fci) was found to be associated with the watery component (H2O). Additionally, these electromagnetic ion cyclotron wave (EMIC) waves can be polarized in both the sense as right and left-handed waves and can get affected in the presence of heavy ions (He+, O+ & N+) (Mauk 1982). EMIC Waves have been extensively reported in Jupiter (Kivelson & Southwood 1996), Saturn (Smith & Tsurutani 1983) and also in comets (Lee 1989) and are believed to be existed in the region where total pressure prevails magnetic pressure. The rate of ion production can be estimated by using the amplitude of the EMIC wave (Huddleston & Johnstone 1992;Cowee et al. 2009) and Loss rate (Hansen et al. 2006;Leisner et al. 2006).
The Wave-Particle Interaction Mechanism – contributes a lot in space and is believed to be of utmost importance mainly in the emergence of the magnetopause boundary layer, auroras, radio wave emissions, energization process etc. Electric and magnetic field components of the wave can exasperate the directions of the particles by scattering them due to their interaction with charged particles within the magnetosphere. The significant outcome of Waveparticle interaction (WPI) takes place only when particle have a cyclotron resonance with wave i.e., There must have a comparable frequency of the wave with one or more of the three occasional motions of the particle (i.e., gyro, drift and bounce), driving the infringement of adiabatic invariants (Thorne 2010). This interaction may lead to energization, landau damping etc. like processes causing damping / growth of wave. Generation of plasma wave instability is another outcome of the interplay between wave and particles where wave enhancement or damping can cause particles to lose or gain energy accordingly (considering their relative velocities). Kennel & Petschek (1966) explained well the (wave-WPI) in view of growth of waves in a very subtle way. Evidence of acceleration and scattering losses as a consequence of WPI is also well demonstrated by Summers et al. (2007). Discussion on WPI outcome is limited here as the study is focused on generation of EMIC is also wave near the equatorial plane.
EMIC wave can be influenced in presence of heavy ions and these waves are classified in three prime frequency band range: Helium ‘He+’, hydrogen ‘H+’ and oxygen ‘O+’, found to be most abundant (Meredith et al. 2014), excitation of which depends on the availability of species (i.e., hot & cold) in the magnetosphere. Remarkable inward radial diffusion of hot components found an extensive event causing ‘growth’ of the ion cyclotron wave (ICW). The event (mixing of hot and cold components) permits an exceptional source of energy-yielding pressure (thermal) anisotropies (T⊥ > T||) of energetic ions (up to few electron volts to thousand electron volts i.e., 10 eV–100 KeV) (Summers & Thorne 2003). Preceding research revealed that the EMIC waves are excited more often in day-side (specifically post noon to dusk) regions (Usanova et al. 2013) due to the blending of the old component from the plasmasphere and hot component of ring.
It is observed that EMIC wave propagating bidirectional (in both the bearings of the equatorial plane i.e., South and north) and ascertained a narrow band (with the thickness of ± 0.1 Rs) near Saturn equatorial plane, manifesting the Doppler shift (Leisner et al. 2011). Two different maxima’s (peaks) in the power spectrum have been found in such a bidirectional region; this layer was interpreted as a wave generation region and found to propagate in the northward and southward direction of the equatorial wave generation region.
At Saturn’s magnetosphere, the perpendicular corotation speed of drifted plasma influences ions generated from neutrals of the icy moon and are taken up into ring distributions which are unstable to grow ion waves of low frequency.
The inner magnetospheric plasma correlates with Saturn (Wilson et al. 2009) and thus the neutral particles emitted by Enceladus move significantly faster at their local Kepler velocity. Many pioneers demonstrated how the convective electric field (the injection velocity) relates to the difference between magnetospheric plasma bulk velocity and neutral particles Keplerian velocity. This is evident that a ring distribution is created by absorbed ions in velocity space (e.g., Coates 2004).
2. Ring distribution and Satellite’s flybys
The ring distribution of ions is unstable to produce a lowfrequency ion cyclotron (left-handed polarized wave) just below the local ion frequency. It is observed that the newly born ions (due to the ionization process) get fully integrated into the flow of Saturn ambient magnetospheric plasma as process showing the conversion of ring distribution into a shell-like distribution and then into Maxwellian distribution by significant velocity diffusion (Szegö et al. 2000;Cowee et al. 2009). All three Pioneer 11 (1979), Voyager 1 (1980), and Cassini (2004–2017) reported ICW in the magnetosphere of Saturn. Pioneer, 11 vector helium magnetometer, has given the extensive view on ICW within inner magnetosphere in close proximity of Dione lying at 6 L.
Prior studies recommended the pickup of oxygen ions as a source of these EMIC waves generated near the equatorial plane. Additionally, Barbosa (1993) determined the ion cyclotron wave, originated due to temperature anisotropy in the near-equatorial region from radial distance 5 Rs to 7 Rs using data from Voyager 1, showing a similar band of frequencies (close to the gyrofrequency of O+), Rodríguez- Martínez et al. (2010) also confirmed ICW and harmonics generated due to temperature anisotropies within the middle magnetosphere. Many pioneer investigators reported the generation of ‘Ion cyclotron wave’ in the intrinsic Saturn environment (Leisner et al. 2006;Rodríguez-Martínez et al. 2010;Meeks et al. 2016).
Consequently, in our present work, we dissected the development pace of EMIC waves along the equatorial plane of Saturn. As referenced before, there are numerous species of particles and wave connections in Saturn’s magnetospheric plasma (Frank et al. 1980), statistical techniques have been found more advantageous to introduce a macroscopic depiction of the plasma wonder. The kinetic method and drift kinetics method were developed by Lee & Kaw (1972) and were utilized by Inhester (1990), showing that the outrageous growth rate (GR) is diminished because of warm impacts. This underlines the requirement of Kinetic approach to treat issues. To characterize plasma instability conditions and GR, we used kinetic approximations given by Brinca & Tsurutani (1989a, b). Thorne & Summers (1989) used the analytical method to best study the waveexcited linear phase. Driven by the above literature, the current evaluation has been employed to obtain the dispersion relation wherever the dependency of wave growth is governed by dimensionless integration using a ring distribution function. In the case of Saturn’s relativistic effects, ion cyclotron instability plays a crucial role in wave-WPIs (Summers et al. 2007). Therefore, we introduce a relativistic effect in the equation to enhance the time GR. Studies show that the lower wave number spectra are affected by the loss cone distribution of particles and these waves increase till 1° (Kumari et al. 2018). Many pioneers such as Pandey et al. (2008), Pandey & Singh (2010) etc. have studied characteristics of EMIC waves using kinetic approach by distribution functions like kappa distribution and generalized distribution. Based on previous literature, this work has been further extended to the ring distribution effect on ion cyclotron waves.
3. EMPIRICAL DISPERSION MODEL
Electric and magnetic fields have direction along the z-axis, with magnitude and EF is presumed in the environment of an anisotropic, homogeneous, and collision-less plasma. Inhomogeneity over micro scale is supposed to have in interaction zone in this specifically.
The involvement of the Vlasov equation helped us reach the perturb state of particles (avoiding higher -order terms), deriving perturbed trajectories of particles alongside bothered conveyance work. Conductivity tensor and dispersion relation for a relativistic case with an effective AC EF for n = 1, have been derived here. The method is completely linear and analogous to the technique used by Kumari & Pandey (2019) and Shukla et al. (2021).
Thus, using eqn 9 given by Kumari & Pandey (2019), Dielectric tensor is given as:
Where, β is the relativistic factor and is defined as For propagation of electromagnetic waves, the general dispersion relation reduces to where . The dispersion relation for the relativistic case with parallel AC EF is written as:
where, subscript s’ denotes type of species i.e., electrons and ions. The ring distribution function is assumed to be the distribution function of the trapped particles (Wu et al. 1989;Kumari & Pandey 2018).
where , are the associated parallel and perpendicular thermal momenta of electrons and ions respectively. ns / n, in Eq. (3) represents the ratio of particle total density captured and characterized by high energy, and erfc(x) in Eq. (4) is a complementary error function. The drift velocity is represented as υ0.
Substituting and using expression (2) in Eq. (1) and after solving the integrations, we get the dispersion relation as:
The above dispersion relation is now approximated in the ion cyclotron range of frequencies.
Electron’s temperature is assumed to be and magnetised with, .
Whereas ions are assumed to have the condition and .
So, considering these approximations, Eq. (5) becomes:
where,
and
After using the charge neutrality condition and the condition Dispersion relation reduces to -
Now the function , stands for plasma dispersion where,
Now the function , stands for plasma dispersio.
Now, dimensionless parameter wave vector is introduced.
In the parallel direction to magnetic field, real frequency and GR are expressed as:
The real part of Eq. (8) is
In the oblique direction to magnetic field, real frequency and GR are expressed as:
The real part of Eq. (11) is
4. RESULTS AND DISCUSSION
To analyse the enhancement rate of EMIC wave at 5 Rs (the region of peak density), influenced by ring distribution in the Saturn inner magnetosphere, given plasma parameters have been considered. An extensive survey of Saturn plasma electron environment done by Sittler et al. (1983) in view of Voyager flybys. An EF Eo = 0.01 mV/m, electron density (no) =5 × 106 m–3 . Though electron densities are found to be extremely variable (decreasing with increasing radial distances) between 3 Rs to 9 Rs due to centrifugal outward transport of plasma, evaluated by Persoon et al. (2005) using Cassini data and ambient magnetic field Bo = 184 nT has been taken into account. The range of alternating current (AC) frequency for background plasma is 4 Hz to 12 Hz and temperature anisotropy AT is assumed to change from 0.25 to 0.75. Barbosa (1993) reported variance in temperature anisotropy (from 1 to 3) due to an anisotropic distribution of pickup O+ ions in the intrinsic magnetosphere, causing wave growth with peak amplitude ~2 nT near the equatorial plane in the view of Voyager 1 observation. Young et al. (2005) and Rymer et al. (2007) have done substantial studies on colder (Approx. less than 100 ev) and hotter (Approx. greater than 100 ev) components to be radially diffused outward and inward, respectively, in respect of centrifugally-oriented instability (Interchanging of these components through transportation) and energy-specific penetration. KBTll is taken to be 200 eV for background electrons depicting thermal energy and 1 keV for isotropic energetic ions (Pandey et al. 2008).
Fig. 1(a) Depicts the variation in GR for parallel traversing ion waves with respect to the magnetic field for numerous values of ‘AC frequency’ (υ) versus ‘wave number’ ( ). The GR γ / ωc = 0.145 is achieved at (0.42) for υ = 4 Hz. For the value of alternating frequency υ = 8 Hz, the maxima appear to be shifted towards = 0.44 with γ / ωc = 0.169. When υ increased to 12 Hz, maximum GR is achieved i.e., γ / ωc = 0.183 at (0.46). In the case of GRs, the spread of the spectrum at lower frequencies is accompanied by a peak shift from 0.42 to 0.46 (due to the Doppler shift resonance condition) occurring in the Saturn magnetosphere. Fig. 1(b) considers oblique propagation of waves and shows variation for different AC frequency values. As it is evident from the graphs that oblique propagation of ion cyclotron waves gives rise to first and second order harmonics. The first harmonics occur at γ / ωc = 0.178, 0.169, and 0.141 with constant values of wavenumber (0.45), for increasing frequencies from 4 Hz to 12 Hz, which is approximately close to the magnitude of GR for parallel propagating EMIC waves. However, the second harmonics arise at an extremely higher wavenumber side with an enhanced peak GR. The value of the maximum peak appears at γ / ωc = 1.425 for υ = 12 Hz at (1.2). The peak seems to be shifted to the lower wavenumber side from (1.2) to (1) as AC frequency decreases to 8 Hz, then to 4 Hz. The contribution of the AC frequency reduces the upper limit of the wave number. This indicates that the presence of a minimum of the parallel AC field frequency is sufficient to trigger instability of the ion cyclotron. The results are consistent with the normalized GR of the ion cyclotron wave of the perpendicular AC field considered in the magnetosphere (Pandey & Singh 2010).
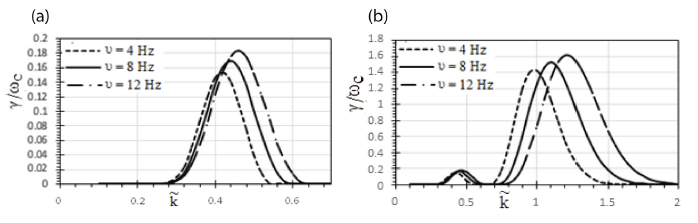
Fig. 2(a) and 2(b) shows the change in the GR of different pressure (temperature) anisotropy values with respect to the wave number for parallel propagation. In above derivation term ‘T⊥ / T||’ equate AT + 1. Thus, for pressure anisotropy T⊥ / T|| (1.25), the maximum G. R. γ / ωc = 0.165. For pressure anisotropy T⊥ / T|| (1.5), GR γ / ωc = 0.169. Similarly, for pressure anisotropy T⊥ / T|| (1.75), the GR γ / ωc = 0.171. For most of the pressure (temperature) anisotropy values, the maxima appear at (0.44). Conclusively, as a ratio of temperatures, T⊥ / T|| increases, and when a wave propagates parallel to the ambient magnetic field, the GR of the EMIC wave increases. Earlier discussed parallel case does not indicate ample variation, but temperature anisotropy is supposed to promote oblique propagation as second harmonics appear at greater γ / ωc along with wide bandwidth spectrum. This propagation shows its highest peak at 1.611 for (1.15) and enhances as the value of temperature anisotropy increases. It can be said that the temperature anisotropy enhances the GR by acting as a source of energy. For ions, EMIC waves are thought to act as whistler waves as on electrons. Thus, temperature anisotropy is considered to be the foremost source of free energy to the plasma.
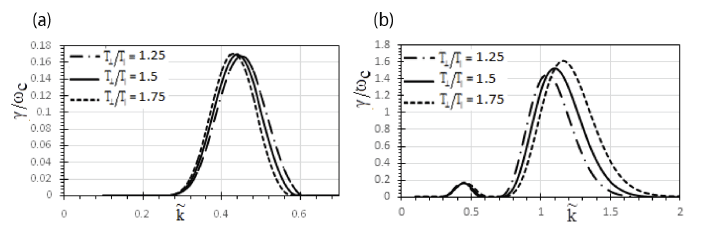
Fig. 3(a) shows the change in the GR for parallel propagating waves to magnetic fields with respect to for various values of the relativistic factor β. For β = 0.5 and β = 0.6, γ / ωc = 0.169 and γ / ωc = 0.161 at (0.44) and (0.43) respectively and at β (0.7), γ / ωc = 0.157 at (0.42) has been calculated. The corresponding value maxima shift from 0.44 to 0.42. As the propagation of waves is changed to oblique, the growth of waves shows double harmonics. However, Fig. 3(b) studies oblique propagation of EMIC waves. Broadening of the wave spectrum and shift to lower wave numbers for higher values of the relativistic factor is clearly visible in the graph. Although in this case also, second harmonics peaked to higher GR under same conditions. For relativistic factor β = 0.5, first peak occurs at γ / ωc = 0.169 for (0.45) and second peak appear at γ / ωc = 1.526 for (1.1). Similarly, for β = 0.6 and 0.7, second harmonics appears at γ / ωc = 1.491 and γ / ωc = 1.454 with (1.05) and (1) respectively. Thus, the above figures, it can be inferred that the relativistic factor does not support growth of waves. Kumari et al. (2019) also quoted similar results for whistler-mode waves. Therefore, the higher s the energy of the particles, the smaller is the magnitude of the relativistic factor causing more ion cyclotron wave growth.
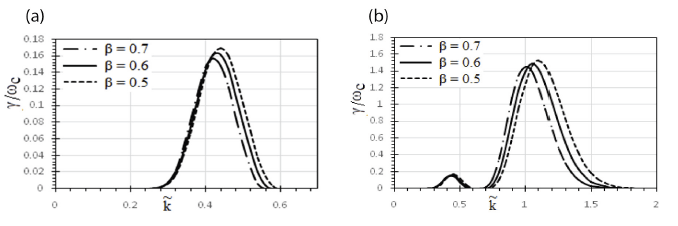
Fig. 4(a) and 4(b) show the varying GR of ion cyclotron instability at various Eo values. We can deduce by seeing the figure that when we study the ring distribution in the magnetosphere of Saturn, the enhancement in EF strength does not promote the growth of the electromagnetic ion cyclotron instability, and it is in the whistler case where Loss cone distribution support the unstable acoustic modes (Kumari et al. 2018). Similar results were shown when the ion cyclotron wave was studied using particle analysis by Ahirwar et al. (2006). Second-order harmonics are also discussed in this study. It can be said that higher-order harmonics affect higher WN (wavenumber) spectra. Fig. 4(b) shows the variation of the oblique propagation of the wave and inferred that the GR is significantly affected by the change in the amplitude of the EF and widens the higher wavenumber side.
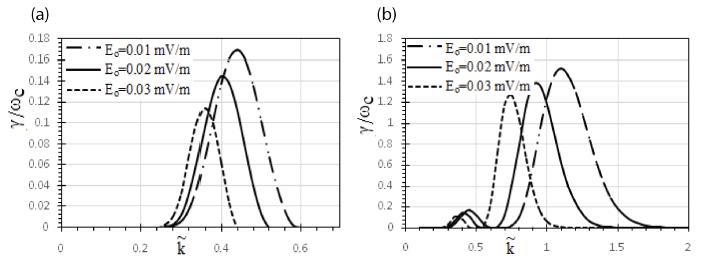
Fig. 5. Explicating the GR of EM ion cyclotron waves for numerous values of pitch angle (PA) (θ, angle of propagation) of wave. As PA increases, the GR is found to be increased more (from 0.169 to 0.171) for the first harmonics, as the PA ranges from 1o to 3o alongside shifting of (from 0.45 to 0.5). A very minute comparative study has been done by Blanco-Cano et al. (2001a, b), showing maximum growth for AC‖ EFs with increased wave number. Hence, the graph also shows second harmonics with the highest peak values as γ / ωc = 1.596 for 3oθ, γ / ωc = 1.556 for 2θo and γ / ωc = 1.526 for 1θo at (1.25, 1.15, and 1.1) respectively. Cowley et al. (2006) have also reported a greater GR for parallel propagation in comparison to oblique, when examining obliquely propagating ion cyclotron waves produced due to ionization of neutrals coming about in pickup particles in Saturn’s magnetosphere.
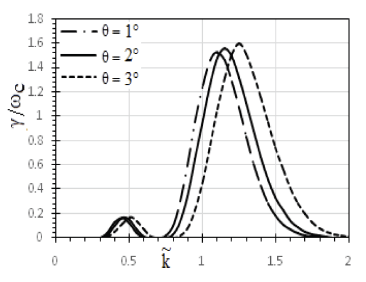
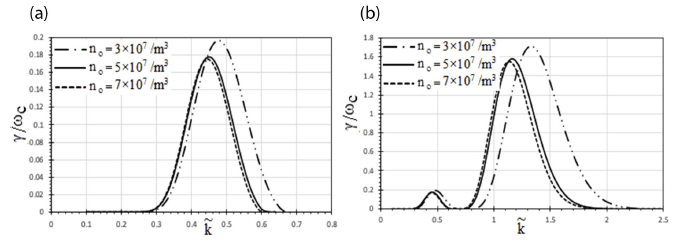
Fig. 6(a) and 6(b) show the graph for the GR of ion cyclotron waves versus wave number for different values of ion density. In Fig. 6(a), for parallel propagation, GR has been plotted against ion number density –3 × 107 m–3, 5 × 107 m–3, and 7 × 107 m–3. It can be seen that γ / ωc = 0.196, 0.175, and 0.173 at (0.48, 0.46, and 0.44) respectively. In Fig. 6(b), for oblique propagation, the GR changes from 1.708 to 1.551 while evolving higher ion density from 3 × 107 m–3 to 7 × 107 m–3 with shifting of wave-number towards lower side i.e., 1.35 to 1.15 thus decreasing the wavenumber indicating the occurrence of multiple harmonics at the same instant. Therefore, as the ion number density in plasma systems increases, the GR of ion cyclotron waves decreases. Ion number density is related to ion plasma frequency and it is also related to the mass of the ion, which is greater than the electron. Electromagnetic ion cyclotron wave ions dominate. Conclusion made is analogous to the analysis done by Kumari & Pandey (2018).
5. CONCLUSION
EMIC waves are believed to be responsible to invoke ion acceleration in magnetic layers and usually observed on the auroral channels of the terrestrial magnetosphere (Ashour- Abdalla & Thorne 1978;Kintner et al. 1978;Lysak et al. 1980), of Jupiter (Cowley & Bunce 2001) and of Saturn observed by HST and Cassini during high latitude pass. These can be found far away from the reason source. The heating effect of ions could also be understood in terms of free energy source (Mitchell et al. 2009) within Saturn. The physical origin of these auroras is yet to be understood in all outer planets. In this framework, considering the ring distribution, oblique (very low angle) and parallel propagation of electromagnetic ion cyclotron waves is reviewed. Using the linear dispersion relation, the expression of the GR of the wave and magnetic field interacting with the wave is derived. Result analysis depicts enhanced GR for greater temperature anisotropy and it is also found to be elevated with increased AC frequency, but GR seems not to be much affected for parallel propagation. It is also being observed that the extent of the EF, relativistic factor does not favour GR. As , if velocity of energetic particles is more, magnitude of the relativistic factor will be reduced inferring more wave growth i.e., particles with more energy will contribute more to grow as compared to the particle of lesser energy. Hence for higher β, GR found to be decreased. This study is based on the wave-WPI and transformation of energy from the particles to wave and growth of wave has been analysed rigorously. Observing the EMIC wave interaction with ring particles in magnetosphere of Saturn near equator, it is seen that as the wavenumber increases, the bandwidth raises towards higher wavenumber side, and the GR attains the highest peak with increasing value of temperature anisotropy. Therefore, it can be inferred that electromagnetic ion cyclotron instability assuming the ring distribution of particles, affects the spectra’s greater wave numbers and gives rise to second harmonics for oblique propagation. Inequality in magnitude of maximum GR is also observed i.e., GR for parallel propagation shows slightly smaller value than the oblique propagation for each condition.
The study mainly concerns about grown waves linked with the distribution of energetic ions and electrons within Saturn inner magnetosphere and could bring significant conceptual developments in the mechanism of generation method (reflecting magnetospheric local processes and complex structure), involving various parameters causing GR and can put forward to evaluate various instabilities, compositional evaluation and scattering losses (as also suggested inside 6 L by Leisner et al. 2006, Rymer et al. 2007) in a different magnetospheric plasma environment including comets. More substantial analysis of EMIC wave origin remains for future investigation.









