Moment of Inertia of Gas as a Source of Added Gravitational Field in Galaxies

1. INTRODUCTION

The rotational dynamics of gas and single stars outside a galactic disk fail to agree with computations as the gravitational potential expected from the distribution of visible mass around a galaxy would not be enough to produce observed velocities (Zwicky 1933;Zwicky 1937;Rubin & Ford 1970). To account for this discrepancy, dark matter was hypothesized to provide the lacking gravitational potential while only experiencing gravitational interaction with matter (Volders 1959;de Blok & McGaugh 1997;Weidinger et al. 2004;Asadov & Kechkin 2009;Albuquerque & Heros 2010). That hypothesis, straightforward as it may appear, faced several problems when followed up by observations.

First, no signs of influence of dark matter have been discovered within the boundaries of the Solar system, whether in terms of gravitational influence or in terrestrial experiments searching for dark matter particles (Cassel et al. 2011).

Second, a problem is posed by mass discrepancyacceleration relation (MDAR) as it is specifically visible matter that determines star accelerations in any galaxies (Ludlow et al. 2017). Moreover, a study of the motion of 400 stars at distances up to 13,000 light years away from the Sun discovered no influence of dark matter (Bidin et al. 2012), prompting the conclusion that there is no dark matter inside the galactic disc. The same conclusion can be inferred from the Tully-Fisher relation (Verheijen 2001) that posits the luminosity of a galaxy, proportional to its mass, to be ideally correlated with its rotation velocity. To sum up, the framework of the dark matter hypothesis fails to elucidate why does the more massive dark matter remain outside of the galactic disk rather than collapse inward. The absence of collapse can be possibly explained by the dark matter’s ability to repel itself.

Third, dark matter is distributed in a spherically symmetrical pattern around various kinds of galaxies as suggested by several galaxies possessing polar rings of gas, e.g., NGC 2685, NGC 4650A, A 0136−0801 and ESO 415-G26 (Schweizer et al. 1983). However it should be noted that rotation will rearrange the initial distribution of mass, even a spherically symmetrical one, into an ellipsoid of revolution. Nothing like that is observed in the case of dark matter. Hence it follows that dark matter is possibly stationary and does not revolve around the center of a galaxy.

Fourth, there are no traces of dark matter in ultra-diffuse galaxies NGC 1052-DF2 and NGC 1052-DF4 (Cohen et al. 2018;van Dokkum et al. 2018;Zahid et al. 2018). This discovery prompted the introduction of an additional hypothesis that dark matter would diffuse between proximate galaxies (Moreno et al. 2022), letting it to be considered mobile and disproving the hypothesis that dark matter would exhibit self-repelling behavior.

It can be seen clearly from the foregoing facts that relying on the dark matter hypothesis to explain newly observed phenomena calls for progressively more complicated models of dark matter. In contrast, the Occam’s principle would rather call for coming up with less complex hypotheses to explain the phenomenon.

This study will introduce a modified law of gravitation whereby a gravitational field would arise due to a combined effect of mass and moment of inertia. In the section titled Discussion we will illustrate how the modified law of gravitation is able to explain problems pointed out in the introductory section.

2. METHODS

It follows from observations that outside of the galactic disc, a galaxy will have its rotational velocity curve level off at a constant level v(R) = const as it will no longer depend on the distance from the center of the galaxy. According to the law of universal gravitation this would only be possible if the mass of matter were a linear equation of the distance away from the center of the galaxy:

However, no matter could be observed outside of the galactic disc to fit the required distribution of mass. To provide an example, the de Vaucouleurs’s distribution describes the surface density of a galactic bulge:

where Ʃ_b0, R_e are parameters of the model. Yet, the mass of the bulge remains constant at greater distances:

The surface density of the stellar disc in a galaxy is described by an exponential law:

where Ʃ_d0, r₀ are parameters of the model. Then the mass of the disc can be expressed as:

Similar to the mass of the bulge, it remains constant M_disk = const beyond the visible boundaries of the galactic disc, R > R_vis. As long as the masses of the bulge and the disc experience no variation beyond the galactic disc, they can be ruled out as potential causes of the galaxy’s rotation velocity remaining constant.

As follows from (Neto 2005;Vikhlinin et al. 2006;Einasto 2011), the density of gas comprising atomic and molecular hydrogen can be described using the Navarro-Frenk-White profile:

where ρ₀, R_s are parameters of the model. Total mass can then be determined as:

where R₀ is the distance away from the center of the galaxy at which gas is encountered. It should be noted that the mass of gas, in contrast to the masses of the bulge and disc, never becomes constant even beyond the galactic disc R > R_vis. This distribution of mass is plotted in the left pane in Fig. 1. However, as the plot shows (see the left pane in Fig. 1), the mass of gas is not a linear equation of distance, therefore the mass of gas can be ruled out as a possible cause of the rotation velocity of a galaxy being constant.

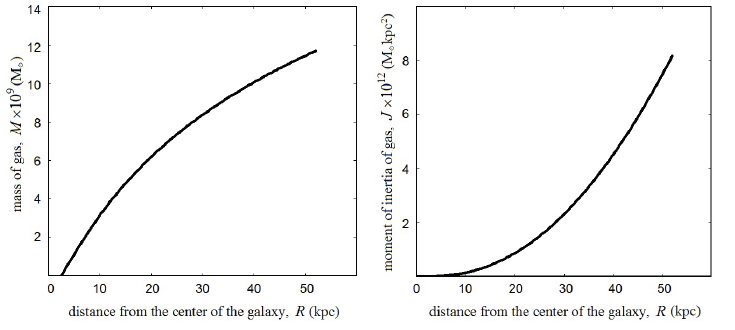
There appears to be no other massive matter that could contribute considerably to the gravitational field of a galaxy. This point was used to advance a hypothesis of invisible dark matter existing beyond galactic disc whose mass would be a linear equation of the distance away from the center of the galaxy M_dark (R) ~ R.

Yet, as indicated in the introductory section, the Occam’s principle applied to dark matter calls for a simpler hypothesis. Therefore we will hypothesize that the gravitational field is not caused by the mass of matter alone. Our previous studies (Portnov 2015;Portnov 2018;Portnov 2021) already entertained the idea of equivalence between equations describing translational and rotational motion. Considering that the inert mass involved in translational motion has an equivalent gravitational mass, we suppose that a similar gravitational counterpart would exist for the moment of inertia which is a measure of inertia in rotational motion. Let us suppose that the gravitational moment of inertia will yield a gravitational field in combination with gravitational mass.

To validate the hypothesis we compute the moment of inertia of gas. For spherically symmetrical matter, the moment of inertia element can be represented as: $dJ=R^{2}dm=\frac{8}{3}{\rho }_{gas}\left(R\right)R^{4}dR$ , which can be expanded as follows by substituting of the equation for density Eq. (3):

The right pane in Fig. 1 shows a plot of the resulting Eq. (5). It can be seen that, in contrast to the plot of mass Eq. (4) approaching a constant value, the moment of inertia will be rising in a non-linear fashion.

Let us assume that the force of gravitational interaction created by the moment of inertia has the following form:

where D is a certain constant of the new interaction, and n is a certain integer. Note that force Eq. (6) is a new radial force proportional to the moment of inertia. It is not related to any known force caused by the bodies' rotation and is not related to the angular momentum of a rotating body. The force Eq. (6) is directed to the center of the system with a moment of inertia J(R).

Now, by analogy with the law of universal gravitation:

we can see that the moment of inertia will appear as a kind of quasi-mass:

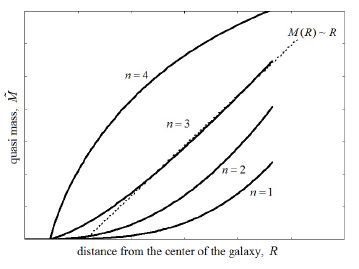
A substitution of the moment of inertia Eq. (5) yields plots of Eq. (8) shown in Fig. 2. As Fig. 2 suggests, the required distribution of mass Eq. (1) is best matched at n = 3.

Thus we can express a generalized law of gravitational influence on point mass m as a combined effect of mass of matter M and its moment of inertia J:

It should be noted that the addend in Eq. (9) as dark matter with a quasi-mass (8).

Then, as a prerequisite for steady orbital motion, point mass m has to move with a velocity:

If the gravitational force acting on point mass is determined by the mass of the stellar disc (2), the mass of gas Eq. (4) and the moment of inertia of gas Eq. (5), then the galaxy velocity curve will be determined by the following equation in accordance with Eq. (10):

3. RESULTS

We consider rotation velocities of three spiral galaxies: NGC 3198, NGC 5033, and NGC 5055. Five rows at the top of Table 1 summarize the parameters of these galaxies.

Triangles in Fig. 3 denote velocities caused by the mass of the gas, computed using the surface density of gas. Diamonds in Fig. 3 denote velocities caused by the mass of the stellar disc, computed using the surface density of the galactic disc. Plotted with error bars is the curve of observed galaxy rotation velocities. These velocities were sourced from (Begeman 1989) for NGC 3198 and from (Haghi et al. 2016) for NGC 5033 and NGC 5055.

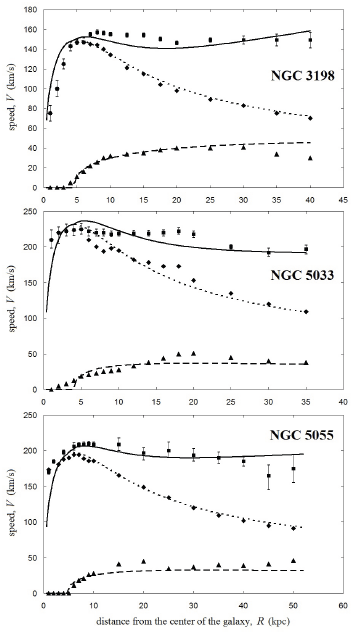
The short-dashed line in Fig. 3 shows velocities computed using the formula:

In this case free parameters Ʃ₀ and r₀ were chosen so as to obtain the closest fit for the curve (denoted with diamonds) plotted using the surface density of the disc. Free parameters Ʃ₀ and r₀ for the three galaxies are listed in bottom rows of Table 1.

The long-dashed line in Fig. 3 shows velocities computed using the formula:

In this case free parameters ρ₀ and R₀ were chosen so as to obtain the closest fit for the curve (denoted with triangles) plotted using the surface density of gas. Free parameters ρ₀, R₀, and R_s for the three galaxies are listed in bottom rows of Table 1.

The solid line in Fig. 3 plots the Eq. (11). The remaining free parameter D was chosen so as to match the observed galaxy rotation curve (error bars) as closely as possible. The bottom row in Table 1 lists interaction constants D for the three galaxies.

The plots (Fig. 3) indicate that velocity curves computed using the model expounded by us in this paper are a close fit of galaxy rotation velocity curves plotted using observational data. Slight discrepancies between simulated and observational curves may suggest density equation profiles of the stellar disc and gas to be more complex than considered in thus paper. Yet, even allowing for this simplification, simulated equations provide a good correlation between the model and observations.

A comparison of interaction constants D for the new interaction across all three galaxies shows these values to be numerically close. By generalizing the resulting values of the interaction constant D for all galaxies under study (Table 1) we determine the mean value of the interaction constant and the random error of its computation:

It should be noted that the constant D for the new interaction is strikingly smaller than the Newtonian constant of gravitation G = (6.6743 ± 0.0002) × 10^–11 N · m²/kg².

4. DISCUSSION

The new gravitational interaction law Eq. (9) sheds light on difficulties faced by the dark matter hypothesis.

First, let us note that point bodies (such as the Sun, planets etc.) will have a moment of inertia J → 0, hence the formula Eq. (9) will approach the classical law of gravitation. This, together with the small magnitude of the interaction constant D (see Eq. (12)) can explain the lack of influence of dark matter in the Solar system space.

Second, gas within galaxies possesses a considerable moment of inertia due to the large dimensions. As a result, the moment of inertia of gas becomes the dominant contributor to the gravitational interaction force Eq. (9) at greater distances, manifesting itself in higher motion velocities of test bodies outside a galaxy that would be expected from mass alone. And this explains why the influence of dark matter becomes apparent only outside of galaxies and not inside them.

Third, an inward collapse of gas into the galactic disc would result in a diminishing moment of inertia dJ = R²dm that would immediately weaken the force of gravitational interaction. Furthermore, it is because of its negligible mass that light gas maintains a spherically symmetrical distribution around galaxies as evident from observations in the X-ray range. This fact explains the spherically symmetrical influence of dark matter.

Fourth, the hypothesis put forward by us explains the lack of traces of dark matter in ultra-diffuse galaxies NGC 1052- DF2 and NGC 1052-DF4. Ultra-diffuse galaxies are galaxies with extremely low luminosity. Their low luminosity is a result of scarcity of star-forming gas, with the galaxy having an older stellar population as a result. It is this extreme scarcity of gas that causes the moment of inertia to be low and any additional influence on the gravitational field to be modest as a consequence. It follows from this reasoning that the stellar component alone explains the dynamics of test bodies around galaxies NGC 1052-DF2 and NGC 1052-DF4.

Note that for R → ∞ it follows from Eq. (5) that J_gas → R² and hence the second term of the right side of Eq. (9) is proportional to R^–1. Since R^–1 > R^–2, then at sufficiently large distances in Eq. (9) there will be F ~ R^–1, and this is the basic formula of Modified Newtonian dynamics (MOND). Therefore, using the assumption that the gravitational moment of inertia enters into the law of universal gravitation, it is possible to obtain the MOND equations.

As an objection to the proposed assumption of the existence of the force Eq. (6) proportional to the moment of inertia, it may seem that the force created by a rotating body is not radial and therefore cannot be added to Newton's law of universal gravitation. But note that the force Eq. (6) is not one of the known forces caused by the rotation of the body, it is precisely the new radial force Eq. (6) proportional to the moment of inertia. As a consequence, the addition of force Eq. (6) with Newton's classical law of universal gravitation is justified.

Note that of course the addition of two forces in accordance with Eq. (9) and the simple model described in this article cannot explain the entire physics of galaxies. However, the described hypothesis of this work can be considered the first step in explaining the dynamics of galaxies.

5. CONCLUSIONS

In this paper we introduced a model of gravitational interaction determined not only by the gravitational mass but also by the gravitational moment of inertia equivalent to the inertial moment of inertia. We show that such a model can explain readily why there is no dark matter inside of a galactic disc and in the Solar system, why does the dark matter not collapse onto the galactic nucleus, and why there are no traces of dark matter in galaxies NGC 1052-DF2 and NGC 1052-DF4.

We used the model to compute rotation curves for three galaxies, NGC 3198, NGC 5033, and NGC 5055. Velocity curves computed for these galaxies fit their observed rotation curves, testifying to the veracity of our model. Thus it can be argued that the gravitational potential of a galaxy is indeed determined not by the mass of matter alone, but also by the moment of inertia of gas.

We believe that the validity of our model can be demonstrated by correlating the observed spatial distribution of density in the stellar disc and in gas surrounding galaxies with a gravitational potential to which the moment of inertia of gas would be a contributor in addition to its mass.