The Possible Signs of Hydrogen and Helium Accretion from Interstellar Medium on the Atmospheres of F-K Giants in the Local Region of the Galaxy

1. INTRODUCTION

It is usually assumed that the stellar chemical composition can be explained only by nuclear processes inside stars. The standard stellar evolution theory proposed by Burbidge et al. (1957) posited that chemical elements with atomic numbers Z > 30 were synthesized mostly in rapid and slow nuclear processes (r- and s-processes) in stars at different evolutionary stages. The interiors of red giant stars were found to be suitable for the s-process, and the astrophysical sites for the r-process are still discussed. Examples of this process include supernova/hypernova explosions and similar rapid high-energy events (Cowan et al. 2021).

Many types of stars with non-solar chemical compositions were discovered in the last decades of the 20th century. It has been shown that the use of only internal nuclear processes in stars to explain the variety of observed stellar abundance patterns, especially for B-F type stars, is not sufficient (Wallerstein et al. 1997;Cowley & Bord 2004). Therefore, several additional scenarios have been proposed, one of which is radiative diffusion in stellar atmospheres (Michaud 1970). Many authors have noted the importance of accretion from the outer space on stellar surfaces.

Different types of accretion from interstellar and circumstellar environments were investigated previously. For example, Fowler et al. (1965) and Proffitt & Michaud (1989) described the influence of mass transfer from evolved binary companions on the abundance pattern of companion stars, while Drobyshevski (1975) and Cowley (1977) discussed the accretion of asteroids and planets, and Venn & Lambert (1990, 2008) noted the dust–gas separation mechanism for λ-Boo type stars. However, the low-intensity accretion of interstellar gas on the surfaces of normal stars remains under investigation. Yushchenko et al. (2015) investigated the possible signs of accretion of interstellar hydrogen and helium in the atmospheres of ρ Pup (δ Sct type star) and several hundred other B-F type stars.

Note that the possibility of this type of accretion was discussed earlier by Greenstein (1949), Havnes (1971), and Böhm-Vitense (2006). The proposed physical scenario is described in more detail in the Discussion section. In this study, we attempt to extend Yushchenko et al.’s (2015) results to stars with lower temperatures. We investigate the dependencies of relative (to solar values) abundances of chemical elements vs. second ionization potentials of these elements in stellar atmospheres with effective temperatures of 3,800–7,700 K. The stellar abundance patterns published by Luck (2015) were used for these calculations. A comparison with similar results for B-F type stars published by Yushchenko et al. (2015) is made, and the directions for possible theoretical explanations of observed effects are discussed.

Yushchenko et al. (2015) investigated only stars with mainly radiative energy transferin the atmosphere. It has been shown that any abundance anomalies in the photospheres of these stars can be conserved on a time scale of several million years (Proffitt & Michaud 1989). The G-K giants investigated in this study also have radiative energy transfer, while the F giants exhibit more significant convective energy transfer. The change in surface chemical abundances as a function of the ratio of convective to radiative energy transfer is the main problem investigated in this study.

2. ANALYSIS OF F-K STARS

For our analysis, we selected the Luck (2015) survey of F, G, and K stars of luminosity class III in the local region. This investigation considered a homogeneous set of stellar parameters and abundance patterns for more than one thousand stars located at distances of approximately 100 parsecs (or less) from the Sun in all directions. The metallicities [Fe/H] are distributed from –2.3 to +1.1 with 98 percent of stars in the range of –0.7 to +0.5. Yushchenko et al. (2015) used the abundance patterns of B-F type stars published by Erspamer & North (2003) and Niemczura et al. (2009) to find the correlations among the relative abundances, projected rotational velocities, and second ionization potentials. For stars with lower temperatures, it is difficult to select the proper spectral line broadening mechanism, including rotation, macroturbulence, or superposition of these effects. Only one of these scenarios was supposed to be valid in the Luck (2015) stars. Therefore, we should omit the investigation of projected rotational velocities, and only the investigation of dependencies between the relative abundances and the second ionization potentials can be made. Note that the rotational velocities of the red giant stars are lower than those of the upper main sequence stars. Therefore, the investigation of red giant rotation requires the highest quality spectra and analysis.

Our results are illustrated in Figs. 1, 2, and 3. The first two figures, similar to Fig. 7 from Yushchenko et al. (2015), show the dependencies of the mean relative chemical element abundances as a function of the second ionization potentials of these elements for twelve star groups with different effective temperatures. Each point in these two figures is the mean relative abundance of certain chemical element calculated for stars with similar temperatures, as listed in Luck (2015).

Fig. 1. Plots of mean relative abundances of chemical elements as a function of second ionization potentials in the atmospheres of 943 stars from Luck (2015) with effective temperatures lower than 5,000 K. The panels represent the groups of stars with different effective temperatures. The temperature ranges and number of stars in each group are noted in the bottom right corners of the panels. The ionizations energies of hydrogen and helium are marked by vertical dotted lines. The atomic numbers of the elements are annotated near the corresponding points. The correlation coefficients of mean relative abundances vs. second ionization potentials are shown. These coefficients were calculated for chemical elements with second ionization potentials in the ranges 12.5 eV < χ <20 eV and χ > 20 eV. The χ ranges are marked in the panels as well as the correlation coefficients.

Download Original Figure

Fig. 2. Similar to the previous figure, but for 206 stars from Luck (2015) with effective temperatures higher than 5,000 K.

Download Original Figure

Fig. 3. Top panel. Correlation coefficients of mean abundances vs. second ionization potentials (χ) for chemical elements with 12.5 eV < χ < 20 eV calculated for star groups with different effective temperatures. Open circles – this study. Dashed squares – Yushchenko et al. (2015). Middle panel. The ratios of radiative acceleration to total acceleration for the Castelli & Kurucz (2003) atmosphere models, calculated for the deepest point in the corresponding atmosphere model as the ratio of two accelerations, tabulated in these models. The ratios were calculated for zero metallicity models with effective temperatures and surface gravities similar to those of the star groups in the top panel. The metallicity of models does not change the interpretation significantly. Bottom panel. Similar to top panel but for chemical elements with χ > 20 eV.

Download Original Figure

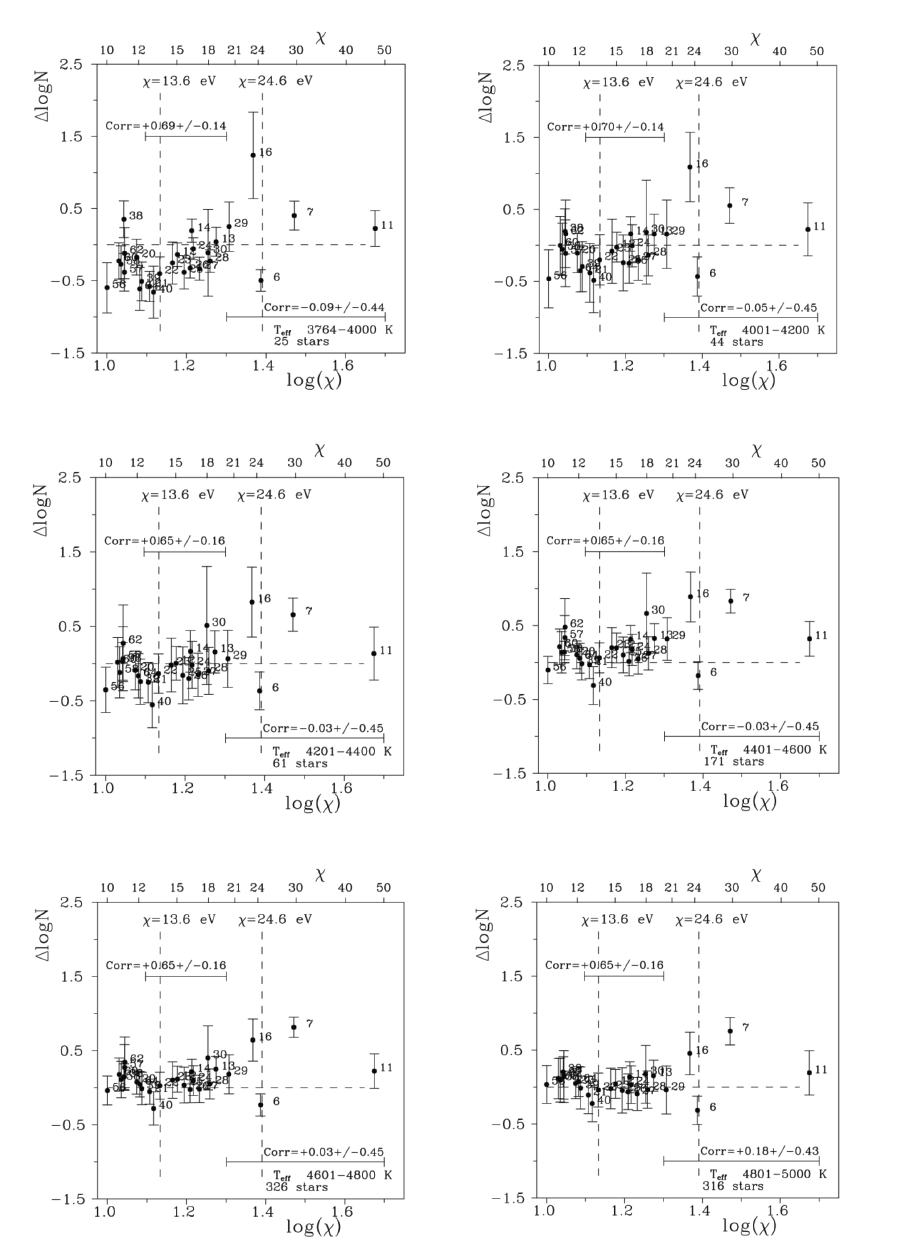
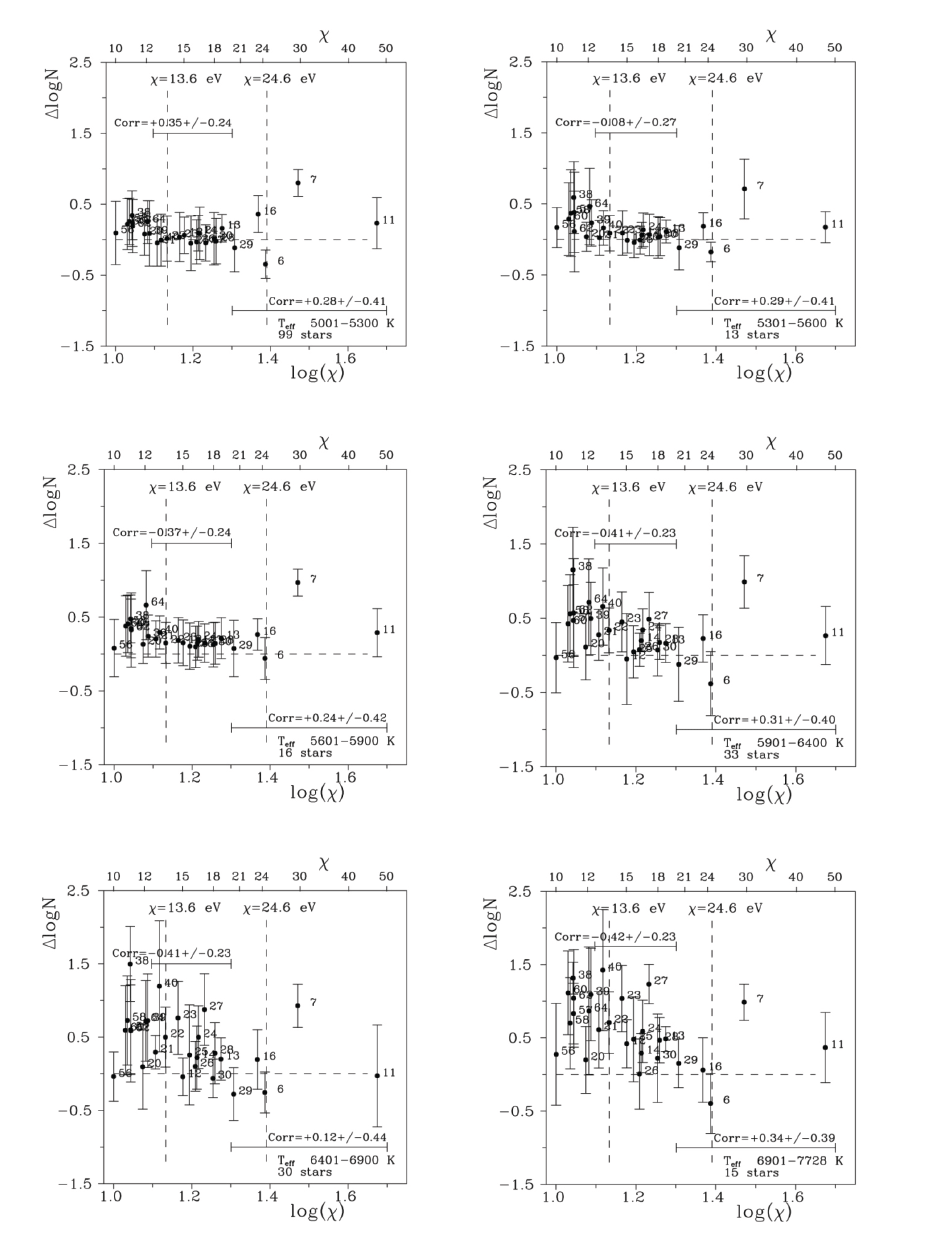
The relative-to-iron abundances for sodium and heavier chemical elements were taken directly from Luck (2015), and the abundances of carbon and nitrogen were adopted as the differences between the absolute abundances, published by Luck (2015) and solar values, published by Grevesse et al. (2010) and Asplund et al. (2021), respectively.

The panels of Figs. 1 and 2 contain the range of stellar effective temperatures, the number of stars, and the correlation coefficients calculated for mean relative abundances of chemical elements vs. second ionization potentials for two groups of chemical elements.

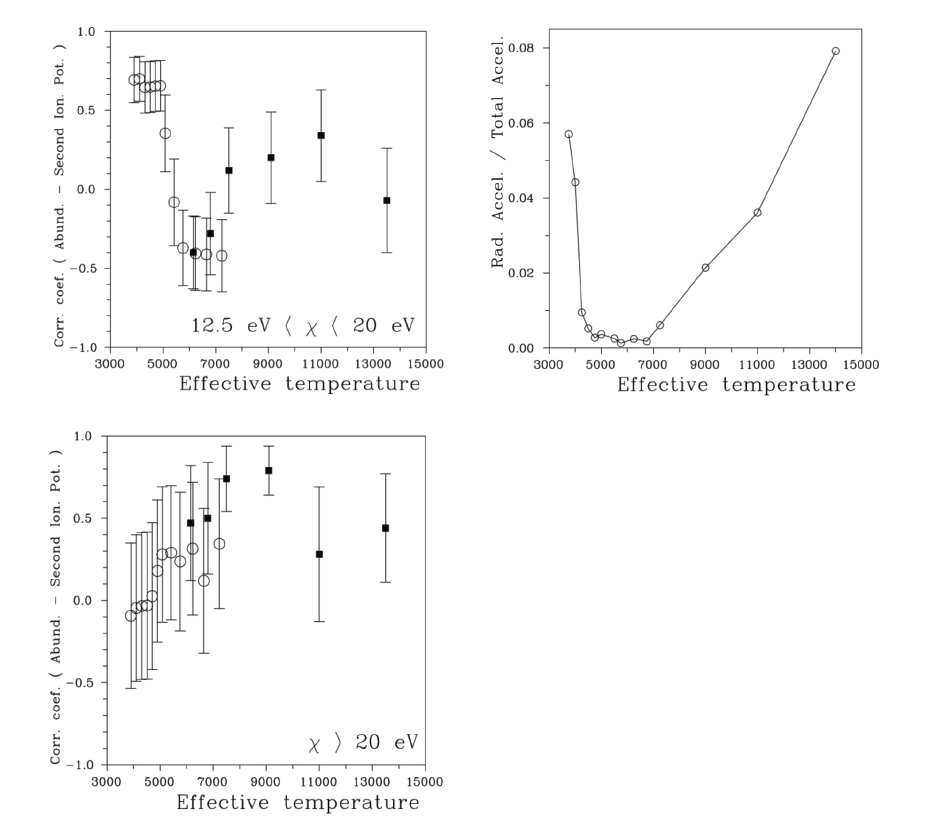
The first group included thirteen chemical elements with second ionization potentials of 12.5 eV < χ < 20 eV; namely, the elements with atomic numbers 12, 13, 14, 21, 22, 23, 24, 25, 26, 27, 28, 30, and 40 (magnesium, aluminum, silicon, scandium, titanium, vanadium, manganese, iron, cobalt, nickel, zinc, and zirconium). The second group consisted of five chemical elements with χ > 20 eV; namely, the elements with atomic numbers 6, 7, 11, 16, and 29 (carbon, nitrogen, sodium, sulfur, and copper). The top and bottom panels of Fig. 3 show the correlation coefficients for the twelve star groups as a function of effective temperature. The results for hotter stars published by Yushchenko et al. (2015) are included for comparison. The middle panel of this figure shows the ratios of radiative acceleration to total acceleration at the base of the atmosphere calculated for the Castelli & Kurucz (2003) grid of atmosphere models. These model parameters were selected to be similar to those of the aforementioned twelve star groups and to those of hotter stars investigated by Yushchenko et al. (2015).

The ratio of radiative acceleration to total acceleration showed the difference between the radiative and convective energy transfer in the stellar photosphere. As it was shown, for example, by Proffitte & Michaud (1989), any chemical anomaly at the surface of a star with mainly radiative energy transfer will be observed for at least several million years. The low part of the convective energy transfer explains the anomaly conservation in the photosphere. The middle panel of Fig. 3 illustrates the well-known fact that the atmospheres of red giants are mainly radiative, as are the atmospheres of upper main sequence stars.

3. DISCUSSION

The upper two panels of Fig. 3 demonstrate that for atmospheres with a high radiative acceleration fraction (with respect to total acceleration), the correlation between the mean relative abundances and the second ionization potential is positive. This means that the effect of lower relative abundance of elements with second ionization potentials close to 13.6 eV, first described by Greenstein (1949), occurs in these atmospheres. The stars with effective temperatures of 5,500 K to 7,000 K have a lower fraction of radiative acceleration. Convection plays an important role in the energy transport in these stars, and (maybe) forces the previously described correlation coefficients to negative values. The stars with the highest effective temperatures namely, higher than 13,000 K, show correlations close to zero. This may be explained by the very different abundance patterns of stars in this range of effective temperatures.

The correlation coefficients of relative abundances vs. second ionization potentials for elements with potentials higher than 20 eV are mainly positive for all star groups, except for the coolest groups. This can reflect the importance of the accretion of interstellar helium in the atmospheres of hot stars. Fig. 3 shows that our understanding of stellar atmospheres needs improvement. The physical process, which has not been previously investigated, results in the described correlations. Accretion can occur through the interstellar medium, other processes, or a combination of several processes.

Notably, the theory of accretion from the interstellar medium has not been developed in detail. The observational results published by Böhm-Vitense (2006), Yushchenko et al. (2015), and Jeong et al. (2019) for different groups of stars and by Kim et al. (2012), Kang et al. (2012, 2013), Jeong et al. (2017, 2019), Yushchenko et al. (2017a,b), and Yushchenko et al. (2020) for individual stars, as well as this investigation, suppose that interstellar gas accretion should be considered for stars over a wide range of effective temperatures.

As noted earlier, Greenstein (1949) first found a correlation between the relative abundances of chemical elements in the atmospheres of metallic-line stars, including ρ Pup, with the second ionization potentials of these elements. The highest relative deficiency was observed for chemical elements with second ionization potentials close to the ionizing potential of hydrogen, namely, 13.6 eV. He proposed an explanation for this effect by charge-exchange reactions of the first ions of these elements with hydrogen atoms in stellar atmospheres.

The second ionization potentials are important for chemical elements that mainly lose the first electron in the stellar atmosphere. Therefore, the resonance value of charge-exchange reactions can be expected for chemical elements with second ionization potentials close to 13.6 eV for reactions with hydrogen or close to 24.6 eV for the charge-exchange reaction with helium atoms. Note that 24.6 eV is the first ionization potential of helium.

Later, Havnes (1971) and Havnes & Conti (1971) described the case of metallic-line stars with strong magnetic fields. It was proposed that the source of hydrogen atoms could not be the stellar atmosphere, but instead was the interstellar medium. They noted that the braking of rotational velocities of metallic-line stars from the limit of stellar stability to very small values could be the result of the aforementioned charge-exchange reactions with hydrogen atoms from the outer space. This was explained as a result of the high velocities of atoms with resonant values of the second ionization potentials. The resulting high velocities allowed these atoms to exit the star. Note that, as it was found by Böhm-Vitense (2006), if the atoms of certain chemical element are mainly neutral in the stellar atmosphere, the described effect is important in first ionization potential coincidence with 13.6 eV or 24.6 eV values.

Some atoms can exit the star at high velocities, which is why the product of these reactions should also be the generation of cosmic rays with energies less than 20 MeV/ nucleon (Havnes 1971). The amount of energy lost by metallic-line stars while decreasing rotational velocities was found to be approximately equal to the total energy of galactic cosmic rays with the aforementioned energies.

As mentioned above, Havnes (1971) and Havnes & Conti (1971) discussed only stars with initially strong magnetic fields, as strong as 10–20 kilogauss. Their explanation accepted the strong magnetic field as the most important factor in describing the physical condition in the atmospheres of metallic-line stars making it possible to neglect many other effects and to predict rotational braking and cosmic ray emission. Notably, the accretion of hydrogen atoms from the interstellar environment is a low-intensity process. The time scale can be a significant part of the stellar age. Due to the high magnetic field, the cross-section for collecting the charged particles from the interstellar medium can be as large as several hundred stellar radii.

North (1984) found that, at least for Si stars, the loss of their angular momentum during the main sequence evolutionary stage could not be confirmed and concluded that the generation of cosmic rays by means of Ap stars was doubtful. Therefore, the observational effect discovered by Greenstein (1949) was not investigated for the next several decades. Böhm-Vitense (2006) identified the effect of the deficiency of relative chemical element abundances both for elements with a second ionization potential close to the ionization potential of hydrogen and for elements with a second ionization potential close to the first ionization potential of helium (24.6 eV). She claimed the charge-exchange reactions to be an important part of the explanation of these observed effects and highlighted that the discussed stars should have magnetic fields. Böhm- Vitense (2006) noted that charge-exchange reactions are observed not only near the resonant value for hydrogen (13.6 eV), as the hydrogen is the most abundant chemical element, but also near the first ionization potential value of the next most abundant chemical element, helium, with a corresponding energy close to 24.6 eV.

Yushchenko et al. (2015) confirmed the deficiency of ρ Pup, discovered by Greenstein (1949), and found a similar effect for several hundred B-F type stars, and Jeong et al. (2019) noted it for barium stars. The above-cited investigations of individual objects and the results of this study show the necessity of a more detailed investigation of low-intensity accretion from the interstellar medium and the influence of magnetic fields on this process. The detection of similar effects for many types of stars requires the presence of a magnetic field to collect the interstellar gas from a wide region around the star.

Figs. 1–3 show that the correlation coefficient for the first group of chemical elements (with second ionization potentials of 12.5 eV < χ < 20 eV) is positive for star groups with mainly radiative energy transfer in the atmosphere and close to zero or negative for star groups with convective energy transport. As it was shown by Yushchenko et al. (2015) and in earlier publications, the relative abundances in the photospheres of stars with radiative energy transfer are deficient for chemical elements with second ionization potentials of 12.5 eV < χ < 20 eV, and the correlation coefficients of these relative abundances vs. second ionization potentials are positive.

This allows us to expect that the described effect is important in the first case, namely for stars with mainly radiative energy transfer and can be neglected for stars with stronger atmospheric convection.

As noted earlier, Havnes (1971) investigated only strong magnetic fields, but the detection of discussed effects in thousands of stars requires the acceptance of weaker magnetic fields or other effects. Recently, Neiner et al. (2016) found a weak magnetic field for ρ Pup. Weak magnetic fields are detected in many types of stars, including those with radiative and convective energy transport in the atmosphere.

Some possible improvements of Havnes (1971) in the case of weak magnetic fields can be outlined. Previous decades have provided observations of interplanetary gas and dust in different olar system regions, even beyond the heliopause. The hydrogen and helium ions as well as the charged dust particles can be collected by magnetic fields from a cross-section with a size of at least ten solar radii for solar-type stars. However, these ions and particles should not be declined by the heliopause.

The neutral atoms and dust particles are not influenced by magnetic fields, and their cross-sections should be of the order of the stellar diameter. One can expect that for stars with supersonic stellar wind and even a weak magnetic field, such as a solar wind, any charged atoms and dust particles are reflected by the heliopause and cannot reach the star surface. We can suppose that the described accretion is important for stars with lower stellar wind velocities for stars without strong chromospheres. A more detailed investigation of the possible accretion scenario will be presented in the next study. Tanaka et al. (2017) provided an example of a similar investigation. Note that the described effect of observed deficiency of relative abundances for chemical elements with ionization potentials close to 13.6 or 24.6 eV was not discussed in detail. It seems that the cited references represent the full coverage of all research devoted to this problem. The proposed physical explanation can be valid or should be corrected; more observations should be analyzed to confirm or reject it.

Investigating the abundance patterns of other types of stars located in the solar vicinity, in other galactic regions, and in other galaxies is required to collect more information about the low-intensity accretion of interstellar hydrogen and helium in stellar atmospheres. The construction of a new theory requires additional observations.