Ionization of Hydrogen in the Solar Atmosphere

Chae, Jongchul

doi:10.5140/JASS.2021.38.2.83

2021; 38(2):83-92

pISSN: 2093-5587, eISSN: 2093-1409

DOI: https://doi.org/10.5140/JASS.2021.38.2.83

Research Paper

Ionization of Hydrogen in the Solar Atmosphere

Jongchul Chae†

Author Information & Copyright ▼

Astronomy Program, Department of Physics and Astronomy, Seoul National University, Seoul 08826, Korea

^†Corresponding Author Tel: +82-2-880-6624, E-mail: jcchae@snu.ac.kr

© The Korean Space Science Society. All rights reserved. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: Feb 3, 2021; Revised: Mar 26, 2021; Accepted: Mar 29, 2021

Abstract

The ionization degree of hydrogen is crucial in the physics of the plasma in the solar chromosphere. It specifically limits the range of plasma temperatures that can be determined from the Hα line. Given that the chromosphere greatly deviates from the local thermodynamic equilibrium (LTE) condition, precise determinations of hydrogen ionization require the solving of the full set of non-LTE radiative transfer equations throughout the atmosphere, which is usually a formidable task. In many cases, it is still necessary to obtain a quick estimate of hydrogen ionization without having to solve for the non-LTE radiative transfer. Here, we present a simple method to meet this need. We adopt the assumption that the photoionizing radiation field changes little over time, even if physical conditions change locally. With this assumption, the photoionization rate can be obtained from a published atmosphere model and can be used to determine the degree of hydrogen ionization when the temperature and electron density are specified. The application of our method indicates that in the chromospheric environment, plasma features contain more than 10% neutral hydrogen at temperatures lower than 17,000 K but less than 1% neutral hydrogen at temperatures higher than 23,000 K, implying that the hydrogen temperature determined from the Hα line is physically plausible if it is lower than 20,000 K, but may not be real, if it is higher than 25,000 K. We conclude that our method can be readily exploited to obtain a quick estimate of hydrogen ionization in plasma features in the solar chromosphere.

Keywords: atomic processes; Sun: atmosphere; Sun: chromosphere; radiative transfer

1. INTRODUCTION

The solar chromosphere mainly consists of free electrons, protons and hydrogen atoms. The ionization of hydrogen is crucial in the physics of chromospheric plasmas because it is the main source of free electrons in most places and affects the mean molecular weight and internal energy as well as the electric resistivity. In fact, hydrogen ionization can be used as a criterion to define the chromosphere itself; the chromosphere can be defined as the whole of plasmas above the temperature minimum region where hydrogen remains partially ionized. According to this definition, prominences that are located high above the top of the average quiet region chromosphere and seen on the Hα line belong to the chromosphere.

The Hα line emitted by neutral hydrogen is the most useful probe of the solar chromosphere available from ground-based observations. This line has a broad line core stemming from large thermal broadening due to the light mass of a hydrogen atom. This property makes it relatively easy to construct a narrowband filter optimized for Hα line observations, which is the main reason why Hα imaging observations remain exceedingly, popular as illustrated in Fig. 1. When the line width is precisely measured with a spectrograph and the contribution of nonthermal broadening is properly subtracted, the hydrogen temperature can be inferred from this line. This idea was the main motivation for the construction of the Fast Imaging Solar Spectrograph (FISS), which records the Hα line and the Ca II line at 854.2 nm (Chae et al. 2013).

Fig. 1. Illustration of an image of the sun seen through a narrowband birefringent Hα filter. This image was taken in the Big Bear Solar Observatory.

Download Original Figure

The hydrogen temperature was measured in a variety of chromospheric features with the FISS. In solar prominences, the average value of the measured temperatures ranged from 8,700 to 10,000 K, but individual temperature values were as low as 4,000 K at some parts and as high as 20,000 K at others (Park et al. 2013). The mean temperature in an internetwork region of the quiet sun was found to be 7,000 K, and that in a network region was 11,000 K (Chae et al. 2020). The individual temperatures measured in the network region were as high as 20,000 K. A sudden increase in the temperature from 9,700 K to 16,000 K was detected in association with the passage of shock waves in Ca II bright grains in an internetwork region (Kwak 2021). In very dynamic features, much higher temperatures were reported. In a surge, the temperature ranged from 20,000 K to 40,000 K with a mean value of 29,000 K (Yang et al. 2013). In an active region coronal rain event, the temperature increased from 10,000 K to 33,000 K as the plasma fell into the sunspot umbra (Ahn et al. 2014). A natural question we have is whether these measured values of the temperature are physically reasonable or not. The major concern is about values of T that appear to be too hot for hydrogen atoms to exist. This raises the question of how to determine the ionization degree of hydrogen for a given temperature.

How can we infer the ionization degree of hydrogen in the chromosphere? The Saha equation is not applicable to the chromosphere because chromospheric plasmas are not in local thermodynamic equilibrium (LTE). The ionization fraction of hydrogen in the chromosphere is determined when the non-LTE equilibrium conditions of hydrogen populations and the equation of radiative transfer are solved together. This is what was done in the construction of atmospheric models. Each atmospheric model provides a table containing lists of hydrogen populations as well as the height, temperature, and electron temperature, among other factors. The ionization of the fraction of hydrogen can easily be obtained by dividing the proton number by the summation of the proton number and the neutral hydrogen number in the table.

The solar chromosphere abounds with physical processes that cause the temperature and density to deviate from the initial or equilibrium values. Suppose that the plasma temperature and density in a small volume of the chromosphere deviate from the values of an atmospheric model by a process such as magnetic reconnection. This raises the question of how can we determine the fraction of hydrogen ionization in such a perturbed state. The best way is of course to solve the full set of non-LTE radiative transfer equations throughout the atmosphere by taking into account this perturbation of the physical condition. Currently, this is not impossible because the numerical codes for such computations are publicly available to solar researchers, among which are the RH code (Uitenbroek 2001;Pereira & Uitenbroek 2015) used to solve for the radiative transfer only and the RADYN code (Carlsson & Stein 1992;Carlsson & Stein 2002) used to solve for the radiation hydrodynamics. Working with these types of codes, however, is a formidable task. In many cases, it is still necessary to obtain a quick estimate of hydrogen ionization under a perturbed physical condition without having to solve for the non-LTE radiative transfer using complicated codes every time. This need motivates the current work.

Here, we present a simple method to obtain a quick estimate of hydrogen ionization in the solar chromosphere. This method is based upon the assumption that the photoionizing radiation field in the atmosphere does not change with time, not being affected by any local disturbing processes. This assumption is physically reasonable because the radiation field in the chromosphere is basically nonlocal in nature. The radiation field at a point is affected not only by the physical condition of the local volume but also by the physical conditions of the entire atmosphere and is hence not very sensitive to the local physical condition. Under this assumption, the photoionization rate is constant over time, being a function of position only. If the simplifying assumption of a plane-parallel atmosphere is adopted, the photoionization rate depends only on the atmospheric height.

We demonstrate how to determine the photoionization rate from the tabulated data of a published atmosphere model. We will also present a simple equation that can be used to determine the degree of hydrogen ionization when the temperature and electron density as well as the photoionization rate are specified. This equation can be regarded as the non-LTE version of the Saha equation.

2. METHOD

2.1 General Formulation of Transition Rates

For the calculation of hydrogen ionization, we adopt a two-level model of transitions for hydrogen atoms. The low level is the ground level of a hydrogen atom. The energy of this level is set to zero. We assume all hydrogen atoms are at the ground level. This level is indexed by i, and its number density is denoted by n_i. The upper level is the level of ionized hydrogen and a free electron. This level has energy above the low level, ranging from hυ₀ to infinity, depending on the kinetic energy of the ionized hydrogen and the electron, where h is the Planck constant and υ₀ is the threshold frequency of the ionizing photon. This upper level is indexed by k, and its number density is denoted by n_k.

Within the upper level, one can define an arbitrary sublevel with the energy ranging from hυ to h(υ + dυ) for υ ≥ υ₀. This sub-level is indexed by u and its number density is denoted by n_u. By definition, the summation of n_u over all the sub-levels should be equal to the population of the upper level n_k. The excess energy of the sub-level over hυ₀ is determined by the kinetic energy of the proton and the free electron, which can be assumed to follow Maxwell-Boltzmann statistics as in LTE. Thus, the number distribution of the sub-level within the upper level should be identical to the LTE distribution except for the normalization factor such that it can be expressed as

n u = a n u *

(1)

and hence

n k = a n k *

(2)

where the superscript ^* denotes the LTE values, and a is the re-normalization factor to be determined from the requirement that the total number density n_i + n_k should be identical to that in the LTE. We will show below that in fact it is not necessary to specify the value of a for our work.

We consider the bound-free radiative transitions between the level i and the sub-level u. The upward radiative transition rate is given by n_iB_iuJ_υ, where B_iu is the Einstein probability of photoionization and J_υ is the mean intensity of the radiation with frequency υ. The Einstein probability is related to the photoionization cross-section α_υ via $B i u = (4 π α υ / h υ) d υ$ . The stimulated downward radiative transition is specified by $n u B u i J υ$ and the spontaneous radiative transition by $n u A u i$ in terms of the other two Einstein probabilities. In thermodynamic equilibrium $J υ = B υ (T)$ holds, where B_υ(T) is the Planck function. Moreover, the detailed balance holds between the upward radiative transition and the downward radiative transitions, leading to

n i * B i u B v (T) = n u * (B u i B v (T) + A u i)

(3)

for an arbitrary T. Moreover, we have the relationship

n u * / n i * = g u / g i exp (− h v / k T),

(4)

where g_i and g_u are the statistical weights of the two corresponding levels and hυ is the energy difference between the two levels. By combining the above expressions and making use of the functional form of B_υ(T), we obtain the relationships among the Einstein probabilities and the photoionization cross-section.

B u i = g i g u B i u = g i g u (4 π α v / h v) d v

(5)

A u i = 2 h v 3 c 2 g i g u B i u = 2 h v 3 c 2 g i g u (4 π α v / h v) d v

(6)

These are very similar to the relationships among the Einstein probabilities in the bound-bound transitions.

From Eqs. (1) and (4), we obtain

n u = a n i * g u g i exp (− h v / k T),

(7)

which can be used to derive the relationships

n i B i u J v = n i (4 π α v / h v) J v d v

(8)

n u B u i J v = a n i * (4 π α v / h v) J v exp (− h v / k T) d v

(9)

n u A u i = a n i * (4 π α v / h v) 2 h v 3 c 2 exp (− h v / k T) d v .

(10)

By integrating the above quantities over υ > υ₀, we obtain the total rate of the radiative transitions.

n i R i k = ∫ v 0 ∞ n i B i u J v = n i ∫ v 0 ∞ (4 π α v / h v) J v d v

(11)

n k R k i, i n ≡ ∫ v 0 ∞ n u B u i J v = a n i * ∫ v 0 ∞ (4 π α v / h v) J v exp (− h v / k T) d v

(12)

n k R k i, s p ≡ ∫ v 0 ∞ n u A u i = a n i * ∫ v 0 ∞ (4 π α v / h v) 2 h v 3 c 2 exp (− h v / k T) d v .

(13)

Finally, with the help of Eq. (2), we obtain the following:

R i k = ∫ (4 π α v / h v) J v d v

(14)

R k i, i n = n i * n k * ∫ v 0 ∞ (4 π α v / h v) J v exp (− h v / k T) d v ≡ n i * n k * R k i, i n †

(15)

R k i, s p = n i * n k * ∫ v 0 ∞ (4 π α v / h v) 2 h v 3 c 2 exp (− h v / k T) d v ≡ n i * n k * R k i, s p † .

(16)

Note that none of these radiative transition rates depends on a. This confirms that the value of a is not needed to calculate the hydrogen ionization.

The photoionization cross-section of hydrogen from the ground level is given as (Note: Throughout this work, we use Gaussian cgs units unless otherwise specified.)

α v = α 0 (v 0 v) 3

(17)

with α₀ = 6.15 × 10^–18 cm²; hence, we obtain

R k i, s p † = 8 π α 0 v 03 c 2 E 1 (h v 0 k T) = 6.1 × 109 E 1 (h v 0 k T),

(18)

where E₁ is an exponential integral function of order 1. From the Saha equation for LTE equilibrium of hydrogen ionization, we obtain

n i * n k * = 4.15 × 10 − 16 T − 3 / 2 exp (h v 0 k T) n e

(19)

such that we can write

R k i, s p = 2.5 × 10 − 6 T − 3 / 2 exp (h v 0 k T) E 1 (h v 0 k T) n e .

(20)

A similar argument can be made to derive the rate of the collisional recombination n_kC_ki from the rate of the collisional ionization n_iC_ik. For hydrogen ionization, we adopt the expression

C i k = 5.9 × 10 − 11 T 1 / 2 exp (− h v 0 k T) n e

(21)

from earlier work (Cox 2000). By applying the condition of detailed balance to the collisional transitions, we obtain

C k i = n i * n k * C i k = 2.45 × 10 − 26 n e 2 T .

(22)

Note that the determination of R_ik and R_ki,in requires the specification of J_υ, from the full non-LTE computation of the radiative transfer. However, even without knowing J_υ, we can safely assume R_ki,in ≈ 0 in the solar atmosphere because it follows e^–hυ/kT ≪ 1 there and hence

R k i ≈ R k i, s p .

(23)

Under this assumption, it is not J_υ but R_ik that must to be specified. This makes the problem much simpler because it is not necessary to solve the full equations of the non- LTE radiative transfer for J_υ. We will describe below how to determine R_ik from the tabulated data in an atmospheric model.

2.2 Ionization Equilibrium

The condition for the ionization equilibrium is written as

n i (R i k + C i k) = n k (R k i + C k i)

(24)

where C_ik, R_ki, R_ki, and C_ki are specified above as functions of T and n_e, but the photoionization rate R_ik has not yet been specified. Note that it depends on the radiation field, which is determined by the overall structure of the atmosphere.

We assume that the radiation field is stationary and regard R_ik as a function of the height z in an atmospheric model. The atmospheric model can be exploited to specify n_k / n_i, R_ki, C_ik and C_ki as functions of z, using which we obtain

R i k (z) = (n k (z) n i (z)) (R k i (T (z), n e (z)) + C k i (T (z), n e (z))) − C i k (T (z), n e (z)) .

(25)

This formula holds for z ≤ z_t only, where z_t is the top of the chromosphere, but it can be extrapolated to the upper layers because the mean radiation intensity at heights z > z_t is expected to decrease with the height owing to geometrical dilution. By assuming that the dilution factor at a point at z > z_t is proportional to the solid angle of the point spanned by the spherical shell of the mean chromosphere, we can obtain the following approximation of the photoionization rate for z > z_t:

R i k (z) ≈ R i k (z t) (1 − 1 − (R + z t R + z) 2)

(26)

In this equation, R is the solar radius. If we choose z = 10,000 km and z_t = 2,200 km, for illustration, we obtain R_ik(z) / R_ik(Z_t) = 0.855. Once R_ik(z) is determined, it is straightforward to determine the ratio n_k / n_i

n k n i = R i k (z) + C i k (T, n e) R k i (T, n e) + C k i (T, n e)

(27)

for arbitrary values of T, n_e and z. We can rewrite this equation in the form

n k n i = n k * n i * R i k (z) + C i k (T, n e) R k i † (T, n e) + C i k (T, n e)

(28)

by making use of Eqs. (16), (22), and (23). We find that this equation is reduced to the LTE solution when R_ik is set to $R k i †$ . The ionization fraction of hydrogen is then given by

x H (T, n e, z) = n k / n 1 + n k / n i .

(29)

which has its LTE counterpart of

x H * (T, n e) = (n k * / n i *) 1 + (n k * / n i *)

(30)

2.3 Working with Arbitrary Thermodynamic Parameters

Above, the (T,n_e) values were regarded as two independent thermodynamic parameters. From time to time, it is necessary to work with a different set of two independent parameters: (p,T) or (p,ρ). To use the formulae given above, one has to derive (T,n_e) from these, which in turn requires knowledge of X_H. Therefore, one has to solve the entire set of equations together. To link p, ρ, n_e, and T, we make a few assumptions. Helium atoms remain neutral and contribute to p and ρ. Metals are the main donor of free electrons in the temperature minimum regions, where the ionization fraction of hydrogen is very small, but their contributions to p and ρ are negligible. Accordingly, we can write

p = 1 + A H e + x H (1 + 4 A H e) ρ k T m H

(31)

n e = x H + A m (1 + 4 A H e) ρ m H,

(32)

where A_He represents the helium abundance and A_mn_H is the total electron density that is attributed to ionized metals. We set A_He = 0.1 and A_m = 1.0 × 10^–4.

Eqs. (29), (31), and (32) complete the statement of the problem. If any of two independent thermodynamic parameters (e.g., p and ρ) as well as z are specified, we can determine the other parameters (e.g., x_H, n_e, and T) by solving these equations simultaneously. We can obtain the solution iteratively using, e.g., the Newton-Rapson method.

3. RESULTS

3.1 Photoionization Rates

Two atmospheric models have been popularly used to describe the atmosphere of the average quiet sun: the VALC model, Model C (Vernazza et al. 1981), and the FALC model, Model C (Fontenla et al. 1993). As shown in Fig. 2, the two models are very similar to each other except in the transition region from the chromosphere to the corona. The FALC model does not display any ad hoc temperature plateau in the transition region, unlike the VALC model. We also note that the ionization degree of hydrogen in the upper chromosphere is slightly lower in the FALC model than in the VALC model. In fact, the FALC model is a revision of the VALC model, which considered the effect of particle diffusion on the formation of hydrogen lines and helium lines. We will adopt the FALC model for the study of hydrogen ionization in quiet sun chromospheric features.

Fig. 2. Height variation of the temperature in the FALC model and VALC model (a), and ionization degree of hydrogen in the atmospheric models (b).

Download Original Figure

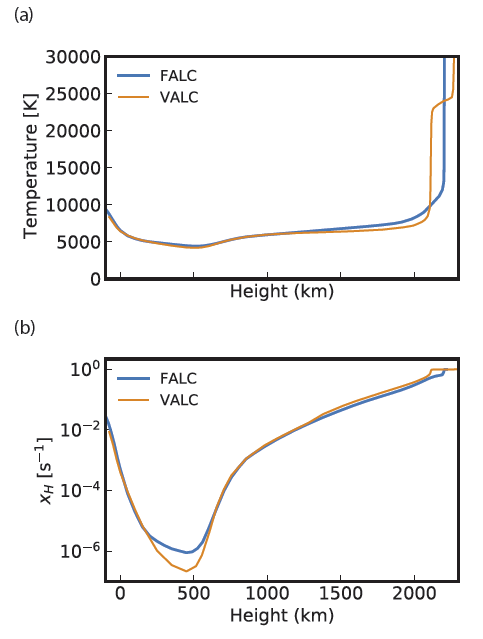
Table 1 lists the values of the photoionization rate R_ik determined from the FALC model at different heights of the atmosphere. In the chromosphere, they range from 7 × 10^–8 s^–1 (at the temperature minimum region) to 7 × 10^–3 s^–1 (at the top of the chromosphere). Fig. 3 graphically presents the height variation of R_ik. For comparison, we have plotted the height variations of the other transition rates as well. We find that throughout the photosphere and the chromosphere, the photoionization rate R_ik is much higher than the collisional ionization rate C_ik. We also find that the radiative recombination rate R_ki is higher than the collisional recombination rate C_ki. Therefore, ionization equilibrium occurs in the form of a balance between two radiative rates: photoionization and radiative recombination. In the transition region, collisional ionization becomes the dominant ionizing process.

Table 1. Table of photoionization rates determined from the FALC model at different heights

Download Excel Table

Fig. 3. Height variations of the transition rates in the FALC model.

Download Original Figure

Our results on the transition rates can be used to estimate the time scale of relaxation τ for ionization equilibrium. The time scale is determined by the summation of all of the rates (e.g., Carlsson & Stein 2002)

τ = 1 R i k + C i k + R k i + C k i,

(33)

which is obviously most affected by the greatest of the four parameters: R_ik, C_ik, R_ki, and C_ki. We find that in the lower chromosphere below 1,500 km, R_ki is dominant. In the upper chromosphere, R_ki gradually decreases with the height while R_ik increases and becomes comparable to R_ki at the top of the chromosphere. As a result, throughout the chromosphere, the sum of R_ki and R_ik has a value of about 10^–2 s, which indicates that the relaxation time is 10² s in the chromosphere.

3.2 Hydrogen Ionization of a Plasma Feature

At this point, we are interested in the determination of hydrogen ionization of a plasma feature where the thermodynamic quantities may differ from those of the atmospheric model at the same height. We thus take only the value of R_ik from the atmospheric model and allow the feature to have arbitrary values of the pressure and temperature. If the feature is at a height of 1,500 km, for instance, we set R_ik to 6 × 10^–4 s^–1 and calculate the ionization degree using the values of p and T.

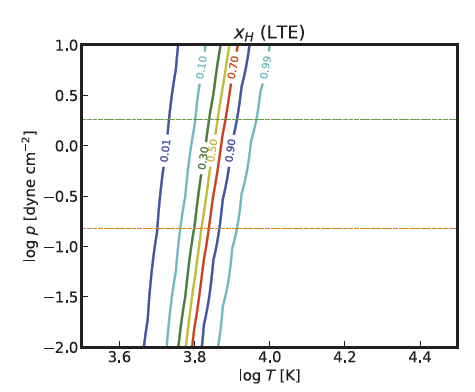
For comparison, we initially examine the result of the LTE calculation. Fig. 4 indicates that in LTE, the hydrogen ionization is very sensitive to the temperature, and the range of temperatures at which both ionized hydrogen and neutral hydrogen exist in significant fractions is very narrow. For instance, in the specific case of p = 0.15 dyn cm^–2, temperature should be in the range of 5,800 K (x_H = 0.1) to 7,400 K (x_H = 0.9). At temperatures above 8,200 K, hydrogen is fully ionized.

Fig. 4. Ionization degree of hydrogen of a plasma feature calculated in the LTE case. The two pressure values at heights of 1,500 km and 2,200 km are indicated by dashed lines for reference. LTE, local thermodynamic equilibrium.

Download Original Figure

The results of the non-LTE calculation shown in Fig. 5 stand in contrast from these LTE calculations. In the middle chromosphere at 1,500 km, x_H is found to be in the range [0.1, 0.9] at T in the range [11,000 K, 17,600 K] when the pressure of 1.8 dyn cm^–2 is used, which is much higher than the range [5,800 K, 7,400 K] in the LTE case. The plasma feature is fully ionized (in the sense of x_H > 0.99) at temperatures higher than 23,000 K.

Fig. 5. Ionization degree of hydrogen of a plasma feature calculated using R_ik = 6.0 × 10^–4 s^–1 at 1,500 km (left) and using R_ik = 7.0 × 10^–3 s^–1 at 2,200 km (right), as obtained from the FALC model. The pressure value of the FALC model at the specified height is indicated by the dashed line in each plot for reference.

Download Original Figure

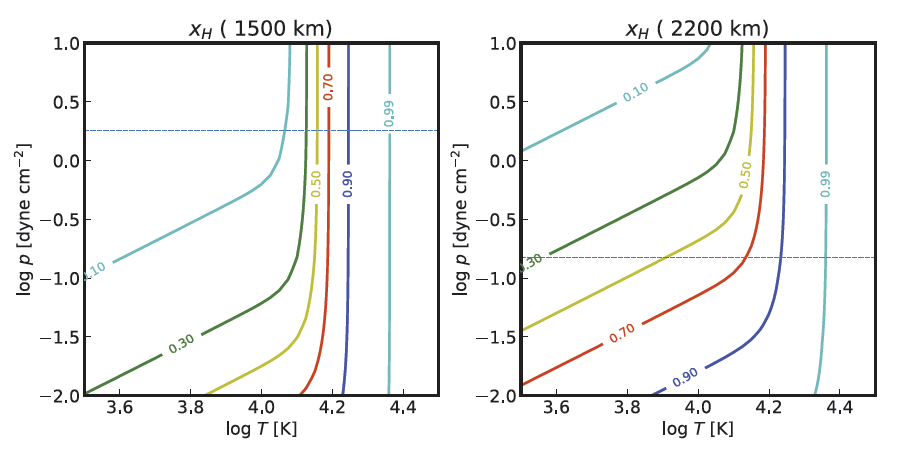
At the top of the chromosphere, the range is broader. The plasma feature contains a significant amount of ionized hydrogen (in the sense of x_H > 0.1), irrespective of the temperature, unless the pressure is too high. The plasma feature also contains a significant amount of neutral hydrogen (in the sense of x_H < 0.9) for temperatures lower than 17,100 K, unless the pressure is too low. As in the middle chromosphere, the plasma feature is fully ionized at temperatures higher than 23,000 K. Note that these specific values of temperature were taken in the specific case of p = 0.17 dyn cm^–2.

The results above are based on the assumption of ionization equilibrium. Because chromospheric features in the upper atmosphere are often dynamic in the sense that position and thermodynamic parameters change rapidly with a time scale of a few minutes, there is a possibility that these features may not be in ionization equilibrium. In order to determine the validity of the ionization equilibrium assumption, we calculated the relaxation time for ionization equilibrium for different values of p and T.

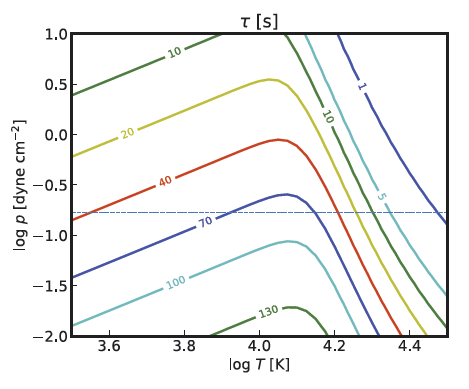
We see from Fig. 6 that higher pressure and higher temperature levels are preferred for ionization equilibrium. The relaxation time decreases rapidly with the temperature, being shorter than 10 s for T > 2 × 10⁴ K in the specific case of p = 0.17 dyn cm^–2. This is much shorter than most dynamic time scales of current interest such that the plasma features of temperatures higher than 2 × 10⁴ K are clearly in a state of ionization equilibrium. In the specific case of p = 0.17 dyn cm^–2, the relaxation time is longest at temperatures around 12,000 K, with a peak value of 80 s. The relaxation times become even longer for lower pressures. Thus, we find that in dynamic chromospheric features with temperatures around 12,000 K and dynamical time scales of a few minutes, the assumption of ionization equilibrium is not fully justified, being in line with an earlier result in the literature (Carlsson & Stein 2002).

Fig. 6. Relaxation time for ionization equilibrium of a plasma feature in the upper chromosphere. The pressure value of the FALC model at 2,200 km is indicated by the dashed line for reference.

Download Original Figure

4. DISCUSSION

By adopting the assumption of a stationary field of photoionizing radiation, we presented a simple method with which to calculate the ionization degree of hydrogen. The equation used here corresponds to a non-LTE extension of the Saha equation for ionization. Once the photoionization rate is determined from an atmospheric model, the equation is applicable to any plasma feature in the atmosphere. As a result, we found that more than 10% of hydrogen can remain non-ionized in a plasma feature for which T < 17,000 K in the chromospheric environment and that most hydrogen becomes ionized at temperatures above 23,000 K.

This result came from the photoionization rates determined from the FALC model. If the VALC model is used instead, the photoionization rate increases by 30% at heights from 1,300 to 2,100 km in the chromosphere. This increase is reflected as a slightly higher value of x_H in the VALC model at heights below 2,100 km, as indicated in Fig. 2. This increase, however, is not significant enough to modify the above conclusion (Note: At heights >2,100 km, x_H in the VALC model is significantly higher than that in the FALC model. This is not due to the higher photoionization rate but due to the higher temperature of the VALC model.), as can be confirmed from the close similarity between Fig. 5 and Fig. 7. This result is not surprising because both the models were intended to describe the same atmosphere — the average quiet sun — despite the differences in the details.

Fig. 7. Ionization degree of hydrogen of a plasma feature calculated using R_ik = 8.0 × 10^–4 s^–1 at 1,500 km (left) and using R_ik = 1.2 × 10^–2 s^–1 at 2,200 km (right) as obtained from the VALC model. The pressure value of the FALC model at the specified height is indicated by the dashed line in each plot for reference.

Download Original Figure

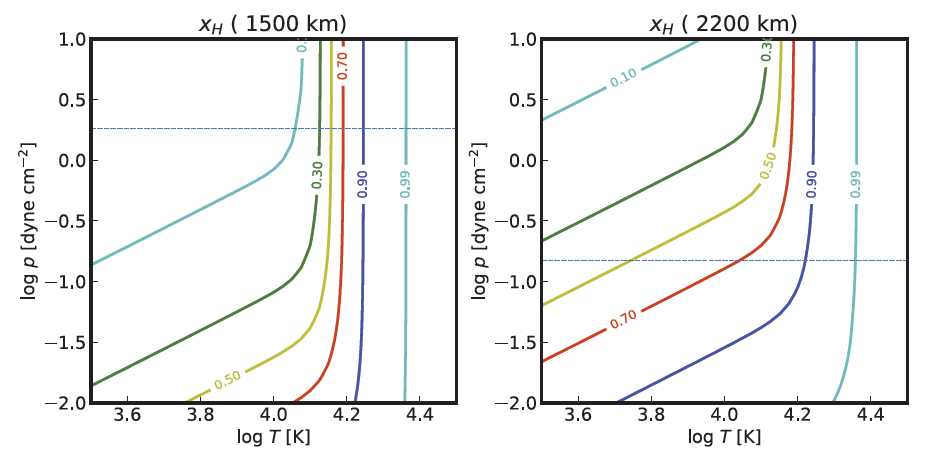
The result above suggests that the values of the hydrogen temperature below 20,000 K reported for prominences, quiet regions, and Ca II grains are physically reasonable but that the temperature values above 23,000 K reported for a surge and a coronal rain event are not. In fact, these features, apart from the Ca II grains, are located high above the top of the mean chromosphere, which is at 2,200 km above the solar surface. Therefore, one may wonder whether or not the above result calculated using the photoionization rate at 2,200 km is meaningful. In principle, we must determine hydrogen ionization using the photoionization rate at the locations of the features. This value can be estimated using the extrapolation described in Eq. (26), which indicates that a feature 10,000 km above the solar surface has a dilution factor of 0.85 for photoionizing radiation, corresponding to a 15% decrease in the photoionization rate. This decrease in the photoionization rate, however, does not cause any noticeable change in the hydrogen ionization and does not alter the above conclusion.

It should be noted that two events, the surge and the coronal rain events, are quite dynamic, either moving upward or downward at high speeds. Therefore, one may resort to the non-equilibrium of ionization to address this discrepancy, as conceived in earlier work (Yang et al. 2013). Our result on the relaxation time scale, however, does not support this argument. It indicates that in a plasma feature with temperatures above 30,000 K, the relaxation time scale can be as short as a few seconds, which is much shorter than the dynamic time scale. Therefore, such a plasma feature is likely to be in a state of ionization equilibrium, with hydrogen being fully ionized. This feature will not be visible on the Hα line because there is no neutral hydrogen at all. Thus, it is very likely that the measured temperatures above 25,000 K may not be real.

We conclude that our method can be exploited to obtain a quick estimate of hydrogen ionization of the plasma features in the solar chromosphere. The method is not sensitive to the specific atmospheric model employed to calculate the photoionization rate. It can be applied to chromospheric features located high above the top of the mean chromosphere as well. The method can be extended even to chromospheric features in other atmospheres, such as a sunspot atmosphere or a stellar atmosphere, where a well-established atmospheric model is available.

Acknowledgments

We sincerely appreciate the referees’ constructive comments, which greatly helped to improve this paper. This research was supported by the National Research Foundation of Korea (NRF-2020R1A2C2004616).

Notes

^{Declaration of Conflicting Interests} The authors declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.

^Funding The authors disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: The project was a sub-study of the project Coming of Age in Exile (CAGE) funded by the Nordic Research Council, NordForsk (grant number 74645).

^{ORCID iD} Jongchul Chae https://orcid.org/0000-0002-7073-868X

References

Ahn K, Chae J, Cho KS, Song D, Yang H, et al., Active region coronal rain event observed by the fast imaging solar spectrograph on the NST. Sol. Phys. 289, 4117-4136 (2014).

Carlsson M, Stein RF, Non-LTE radiating acoustic shocks and CA II K2V bright points. Astrophys. J. 397, L59 (1992).

Carlsson M, Stein RF, Dynamic hydrogen ionization. Astrophys. J. 572, 626-635 (2002).

Chae J, Park HM, Ahn K, Yang H, Park YD, et al., Fast imaging solar spectrograph of the 1.6 meter new solar telescope at big bear solar observatory. Sol. Phys. 288, 1-22 (2013).

Chae J, Madjarska MS, Kwak H, Cho K, Inference of chromospheric plasma parameters on the Sun. Multilayer spectral inversion of strong absorption lines. Astron. Astrophys. 640, A45 (2020).

Cox AN, Allen’s Astrophysical Quantities, 4^th ed. (AIP Press, Springer, New York, NY, 2000).

Fontenla JM, Avrett EH, Loeser R, Energy balance in the solar transition region. III. Helium emission in hydrostatic, constant-abundance models with diffusion. Astrophys. J. 406, 319 (1993).

Kwak H, Impulsive wave excitation in the solar atmosphere, PhD Dissertation, Seoul National University (2021).

Park H, Chae J, Song D, Maurya RA, Yang H, et al., Temperature of solar prominences obtained with the fast imaging solar spectrograph on the 1.6 m new solar telescope at the big bear solar observatory. Sol. Phys. 288, 105-116 (2013).

10.

Pereira TMD, Uitenbroek H, RH 1.5D: a massively parallel code for multi-level radiative transfer with partial frequency redistribution and Zeeman polarisation. Astron Astrophys 574, A3 (2015).

11.

Uitenbroek H, Multilevel radiative transfer with partial frequency redistribution. Astrophys. J. 557, 389-398 (2001).

12.

Vernazza JE, Avrett EH, Loeser R, Structure of the solar chromosphere. III. models of the EUV brightness components of the quiet sun. Astrophys. J. Suppl. Ser. 45, 635-725 (1981).

13.

Yang H, Chae J, Lim EK, Park H, Cho K, et al., Velocities and temperatures of an Ellerman bomb and its associated features. Sol. Phys. 288, 39-53 (2013).