1. INTRODUCTION
Aviation radiation is an unavoidable space weather phenomenon. In Korea, the Environmental Radiation Safety Control Act regulates the annual dose limit for the aircrew. Radiation in commercial airplanes’ altitude is the ionizing radiation originated from the primary protons of galactic cosmic rays (GCR) and solar energetic particles (SEP). It is discovered that accumulated radiation exposure is caused by high linear energy transfer (LET) of those incident energetic particles into the Earth’s atmosphere (Wilson et al. 2005). Radiation by GCR is relatively stable and does not change much. That by SEP is somewhat transient and increasing suddenly with solar activities such as solar flare and coronal mass ejection. So, the resultant aviation radiation exposure is the combination of two main contributions from both GCR and SEP origins. At commercial flight altitude, aviation radiation is the latitude, altitude, and solar activity function. Earth’s magnetic field cuts off the energetic incident particles depending on the latitude. The cutoff rigidity is relatively higher in the equator than the polar region, and the energetic particles can precipitate easily through the polar region.
International Commission on Radiological Protection (ICRP) and International Commission on Radiation Units and measurements (ICRU) have recommended to predict aviation radiation exposure for the air crew’s radiation safety. To satisfy this purpose, various estimation programs such as Sievert, EPCARD, PCaire, and JISCARD were developed, the Federal Aviation Administration (FAA) distributes the CARI-6/6M computer program (O’Brien et al. 2003), and NASA also developed the NAIRAS program (Mertens et al. 2013). While CARI-6/6M considers the GCR contribution, the NAIRAS program considers both the GCR and SEP effects. Currently, FAA develops an updated version of CARI-7 and -7A, including the SEP events. We also develop by ourselves the Korean Radiation Exposure Assessment model for the aviation route dose (KREAM) for radiation safety of the Korean aircrew and passengers (Hwang et al. 2010, 2014). Most advanced countries have their aviation radiation assessment program to assess the aviation radiation exposure of the aircrew and the passengers, and they have continued updating their own programs.
In this paper, we compare the in-situ measurements by using Liulin-6K equipment at the commercial flights with KREAM results to validate the reliability of our aviation radiation prediction model KREAM. We also compare the measurements with the other two models of CARI-6M and NAIRAS. Aviation radiation measurements were performed during the early three months of 2020. Liulin-6K equipment used for our study was initially designed to measure an absorbed dose and a significant dose of space astronauts. Liulin type equipment using a silicon sensor to detect the charged particles’ LET has been continuously improved since it was firstly used in 1988 for the MIR space station (Dachev et al. 2015). Its measurements are known to be reliable not only in space but also in aviation altitude over the polar route (Hwang et al. 2010). This year is the solar minimum period connecting the solar cycle 24 and 25, so it is very proper to verify in-situ data and program because the values are comparably stable than the solar maximum period. Undoubtedly more comprehensive verification of the KREAM program should be performed in the future.
2. EXPERIMENTS
The experiments were carried out 25 times from March 11 to May 26 of 2020. Table 1 indicates the flight information of departure time, arrival time, flight time, departure airport, arrival airport, and maximum altitude for each experiment. Most flights start from or return to Incheon airport (ICN). The flights cover various continents of North America, South-east Asia, Australia, Russia, and Europe. Flight times are written in Universal Time (UT). We can get the GPS information of each route from a flight aware web site (https://flightaware.com). The site offers rough information about air routes for the permitted commercial flights. These geographical data from the web site are critically important, even though some geographic data points are missing. These data gaps were extrapolated to get the continuous flight information of latitude, longitude, and altitude required to run the KREAM model. Using a globally effective dose map originally implemented inside the KREAM program package, the route dose can be produced precisely for each specific flight.
Table 2 shows that the route dose and averaged dose rate are measured by Liulin-6K and geographic information of maximum altitude and latitude for 25 flights. Liulin spectrometer’s primary purpose is continued monitoring of doses, fluxes, and spectra during aircraft flights. The spectrometer can work by internal Li-Ion batteries. Liulin- 6K is a kind of energy deposition spectrometer using a silicon sensor. These semiconductor detectors cannot measure the effective dose directly but can obtain the ambient dose equivalent H∗(10) from the deposited energy in the detector (Green et al. 2005;Spurný 2005;Ploc et al. 2011;Kubančák et al. 2014). The reliability of this conversion method has been verified from numerous previous measurements. But there remains a fundamental limitation caused by the charge sensitive detector of the Si sensor. To solve this problem, we are currently developing a Tissue- Equivalent Proportional Counter (TEPC) equipment, which considers biological effects more sophisticatedly (Malimban et al. 2019). The tissue equivalence principle is based on the fact that the significant parameter in radiation energy transfer is the atomic composition of traversing material.
In contrast, the chemical combination of material elements is not essential. Therefore, human tissue can be replaced with substance providing the same as tissue energyabsorbing properties. Such materials are usually a mixture of hydrogen, carbon, nitrogen, and oxygen. One of these mixtures is A-150 plastic commonly used for the wall of a tissue-equivalent proportional counter. The Counter’s chamber is filled with methane or propane-based tissueequivalent gas. Further experiments using our TEPC are planned to be carried out soon.
3. Analysis
We classified the experiments depending on continents to show the correlation between route dose and geographic information such as flight time, latitude, and altitude. In Table 2, in the case of North-America, a cumulative effective route dose of flights to ICN (from #7 to #12) is 557.02 μSv, which is greater about 15% than that of flights from ICN (from #1 to #6) whose amount is 470.97 μSv. That difference is undoubtedly caused by the difference in flight time. The total flight time of return flights to ICN is 81.8 hours, which is longer about 11% than that of departure flights from ICN, which is 72.6 hours. The time difference is due to the jet stream because the jet stream, which rotates the Earth in a counter-clockwise direction from the top view, pushes or pulls aircraft (Irvine et al. 2016). All return flights to ICN (from #7 to #12) flew above the latitude of 55 degrees, and 50% of these flights (three flights) flew over the altitude of 11.5 km (about 38,000 feet). This is contrasted from the results of departure flights from ICN; there are just two flights out of six flights that flew over the latitude of 55 degrees, and none of these six flights flown over the altitude of 11.5 km.
In the case of Europe, total route doses of departure and return flights are 253.30 μSv and 227.06 μSv, and respectively, the former is more significant, about 11% than the latter. It is also caused by the flight time difference. In this case, the total flight time of departure and return flights is 42.08 hours and 38.2 hours. The difference is about 10%. Also, the latitude and longitude are similar in both the 13th and the 15th flights. The mean effective dose rate of the 13th flight is much higher than the 15th flight because the altitude of the 13th flight is much higher than that of the 15th flight. On the other hand, for the 13th and 14th flight, their averaged dose rates differ about 2 μSv/hr despite the similar maximum latitude. The difference could be interpreted as caused by the difference in flight altitudes. For the 17th and the 21st flights, although the 21st flight flew at high latitude overall, the averaged dose rate is lower than that of the 17th, which flew at low latitude but partially reached higher latitude. It might be explained if flying latitude exceeds a certain threshold, the effective dose might ascend rapidly.
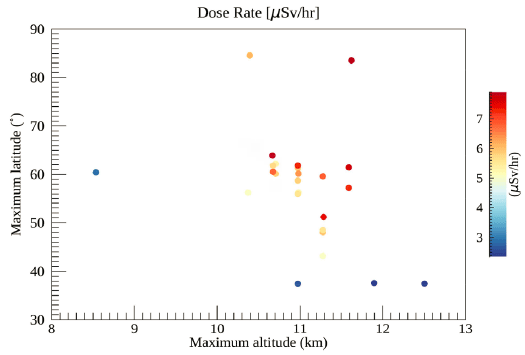
Fig. 1 shows the relative influence of altitude and latitude on an effective dose rate. The X-axis of Fig. 1 is maximum altitude (km), the Y-axis is maximum latitude (degree), and the symbol corresponds to 25 flights. The color-bar range is from 2.39 to 7.9 μSv/hr, and the color indicates the averaged dose rate. In the graph, three bottom-right flights have a relatively high maximum altitude but low maximum latitude, so consequently have a relatively low mean dose rate. On the other way, the leftmost flight has a relatively high maximum latitude but low maximum altitude, so it has a relatively low mean dose rate. Likewise, flights with somewhat high maximum altitude and latitude could reach a relatively high mean dose rate. This interpretation is coincident with the previous result of Ahn et al. (2020). However, we know there is a limitation in this rough interpretation because it is just a simple comparison between maximum altitude and maximum latitude with a mean dose rate. Even we do not consider the longitudinal effect. It is crucial because it is relevant to the geomagnetic cutoff rigidity, which is the critical factor indicating how well the Earth’s geomagnetic field shield the solar wind charged particles by deflecting them back to space, varying with both the latitude and the longitude. It could be improved if we can obtain precise air route information, including the altitude, the latitude, and the longitude. For this purpose, GPS equipment should be accompanied by radiation measurement. We remain more complemented experiments for future work.
We calculated the effective dose using KREAM for the identical 25 flights. Fig. 2 shows the comparison between Liulin observations (green) and KREAM model results (red) for three return flights to ICN. Fig. 2(a), 2(b), and 2(c) are the plots for the return flights to ICN from ATL, FRA, and SGN, respectively. They are typical examples of frequently used air routes of North America, Europe, and Southeast Asia. In Fig. 2(a) and 2(b), the effective dose rates suddenly drop when the aircraft arrives above the airport, even though they still keep their altitude. This might be due to the cutoff rigidity effect. The cutoff rigidity of the area covering ICN is from 5 to 10 GV. It differs so much from that of ATL and FRA, whose amount is about 1 to 5 GV. It means that areas with ATL and FRA are relatively vulnerable to precipitating charged particles of the solar wind. Although the cutoff rigidity is over 10 GV, which is relatively high, as Fig. 2(c) shows that there might be some attenuation of impact of the cutoff rigidity on the effective dose rate when it rises over a certain range in flight altitude.
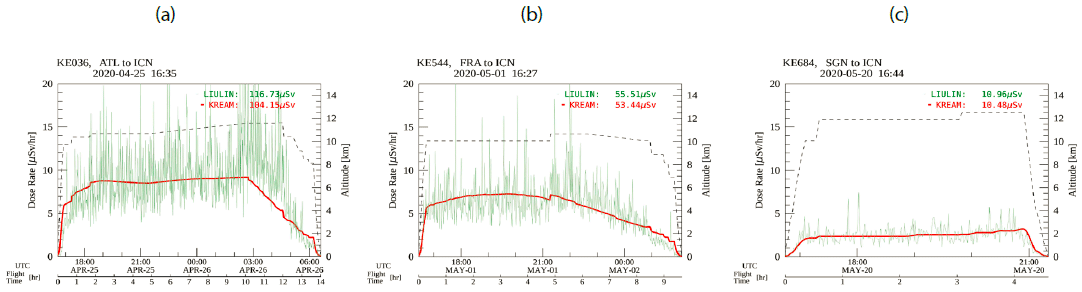
Table 3 describes the total effective dose of in-situ data from Liulin equipment and model values from three different models of NAIRAS, CARI-6M, and KREAM, and shows their percent error between observational data and model run results. The top plot of Fig. 3 shows the total effective dose distribution, and the bottom plot shows their percent error distribution. As shown in fig. 3, NAIRAS (green) results are located higher than all the other models, and observation data and KREAM (red) produces the most similar values with Liulin data (purple). CARI-6M (blue) seems to be located in the lowest region. This tendency becomes the absolute percent error in the bottom panel in Fig. 3. KREAM’s percent error (red) is distributed near the zero lines, and that of CARI-6M spreads out more widely. This spread is most severe in NAIRAS’s percent error (green). The formula to obtain a percent error is as follows.
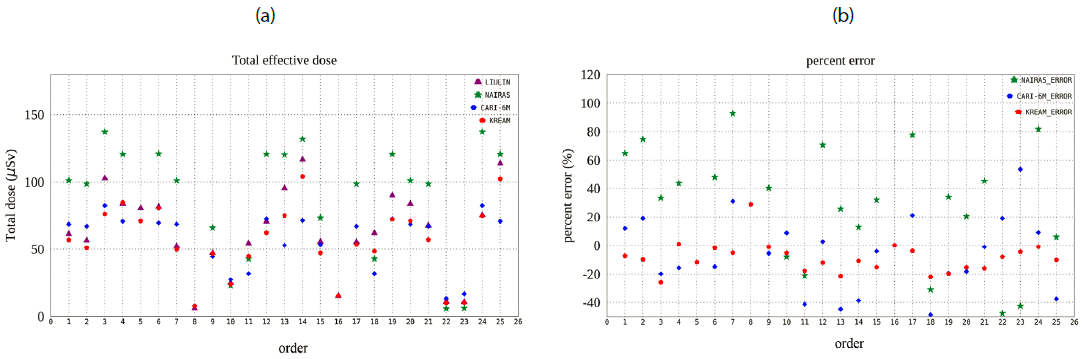
Consequently, KREAM values show the lowest error in 19 cases out of 25 cases, while CARI-6M and NAIRAS are closest to Liulin value in five cases and only one case, respectively. KREAM values show over 20% error in just 4 cases, and the maximum error is 29%, which is under 30%. The number of 30% is critically important because the acceptance level of uncertainty in the radiation estimation program should be 30%, as suggested by the Korea Institute of Nuclear Safety (KINS). In the case of CARI-6M, the error exceeds 40% error in 4 cases, it is located between 20% and 40% in 4 cases, and the maximum error is even 53.5%. In the case of NAIRAS, the error exceeds 60% in 6 cases, it is located between 40% and 60% in 6 cases, which is between 20% and 40% in 7 times, and their maximum error is 92.3% surprising. The averaged errors are 43.38%, 22.03%, and 10.95% for NAIRAS, CARI-6M, and KREAM, respectively. NAIRAS cannot satisfy the acceptance level of uncertainty while CARI-6M and KREAM satisfy that criteria. At the bottom of fig. 3, the error over 0 means model values exceeds in-situ data, and vice versa as a whole, NAIRAS values are higher than Liulin data except 5 cases. In the case of CARI-6M, the values fluctuate up and down around Liulin data, while KREAM values tend to have a little lower value than Liulin data except for 3 cases. Also, as shown in the bottom of Fig. 3, the tendency of the fluctuation of the KREAM value is most similar to that of the Liulin data. It is more important than difference of the values itself, because values which are less than the 30% ICRU/ICRP criterion for dose assessments at aviation altitude can be acceptable (ICRU 2010).
We might interpret why KREAM shows slightly lower values than Liulin data from the uncertainty of both KREAM GPS data and Liulin data. KREAM activates how it temporally produces global dose map first based on GCR and SEP input spectrum and calculates a spatial summation of the effective doses of locations where the aircraft passed. However, some missing data points of locations are extrapolated within known neighborhood data points. Such extrapolation might cause underestimation of radiation exposure calculation of KREAM. We analyzed dose from spatially intact flight route for some flights and confirm that this underestimation somewhat decreases. To solve this problem, we plan to accompany the GPS equipment in the upcoming experiments. Another possibility is due to the uncertainty of Liulin observation itself. In principle, Liulin detects the charged particle only, actually just electrons. It assumes the other particles’ fixed contribution in the aircraft altitude, and that method might sometimes cause overestimation of the real radiation exposure.
In our research, only two experiments corresponding to the 4th and 14th in table 3 are carried out over the polar route to ICN from JFK and ATL. Fig. 4 shows the airways of these two polar flights. Black lines indicate the altitude observation data are missing but we can obtain those from the flightaware website. If we cannot obtain the GPS information both measurement and website, it is indicated as white dotted lines as shown at the bottom of Fig. 4. The 14th flight has too high maximum latitude and maximum altitude, which leads to the highest route dose and mean dose rate among a total of 25 flights, whose amounts are 116.72 μSv, and 7.9 μSv/hr, respectively. For the 4th flight (Polar 1 in Fig. 5), the mean dose rate is not so high as 6.1 μSv/hr even though the polar route. This might be based on the low maximum altitude of 10.39 km. This is the lowest among all experiments over North-America.
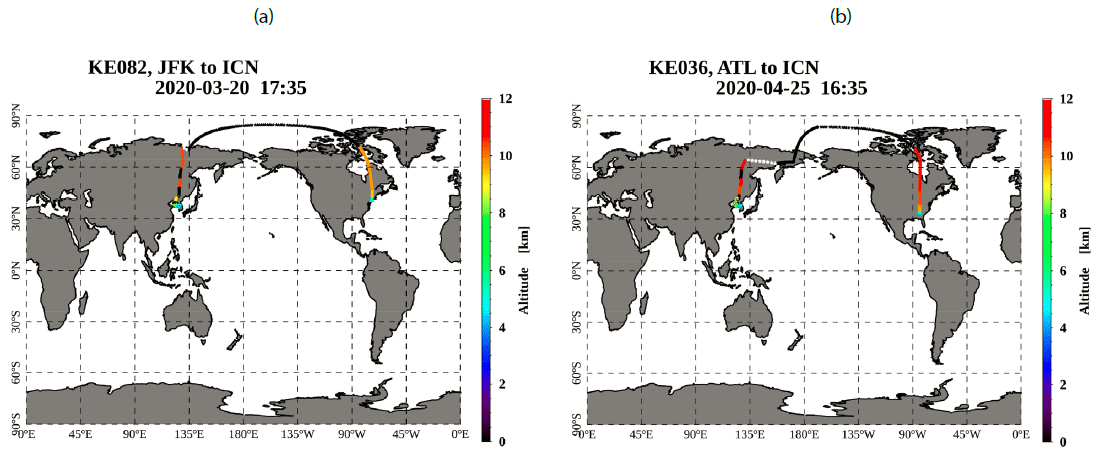
Although both the 4th and 25th flight in table 1 identically took off from JFK and landed on ICN, the 4th flight used the polar route, and the 25th flight did not. In this case, the 4th flight saved about an hour of flight time, and whose route dose and mean dose rate are lower than those of the other flight. It also can be concluded that the altitude plays a significant role in this difference because the maximum altitude of the 25th flight is about 11.59 km, which is the second-largest maximum altitude. And flight time is also an essential factor. The 25th flight takes one hour longer than the 4th flight, and it might cause the more significant route dose of the 25th flight. By this comparison, we can conclude that aircrew and passengers should pay careful attention to the altitude changes during their voyager over the polar route even though a solar event was not predicted. Suppose solar events occur during the flight over the polar route. In that case, there could be a much dramatic increase because many high-energy charged particles (especially protons) might precipitate into the polar region (Mertens et al. 2010).
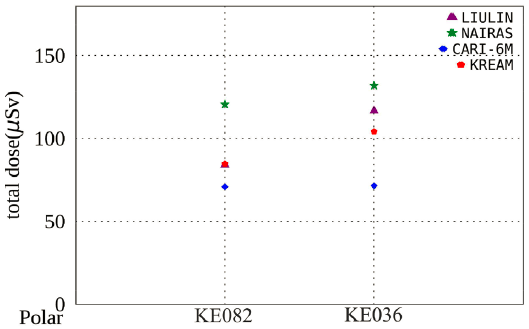
Fig. 5 shows the comparison plot of two polar routes separated from Fig. 3(a). In the case of polar 1 (the 4th in Fig. 3), the KREAM value is very similar to Liulin data because flight route data is linear, as shown in the upper panel of Fig. 4. On the other hand, the KREAM value of polar 2 (the 14th in Fig. 3) is comparatively lower than the Liulin value, which might be because there is missing data around longitude of 140˚E as shown in the bottom panel of Fig. 4. The values of Liulin and KREAM are comparatively higher than those of CARI-6M on both flights. NAIRAS values are much higher than Liulin data. It is clear that there is a general tendency; NAIRAS produces the highest values, Liulin/KREAM has median values, and CARI-6M makes the lowest values.
4. Summary and Conclusion
Recently the necessity of precise prediction and measurements of aviation radiation is increasing in Korea. Several radiation prediction models exist in aircraft altitudes such as NAIRAS, CARI-6/6M, Sievert, EPCARD, JISCARD, PCaire, etc. For our air crew and passengers’ radiation safety, we develop our radiation prediction model, KREAM. In this paper, we validate the KREAM model based on comparison with Liulin observations. We perform 25 experiments to measure aviation radiation exposure using Liulin-6K for the early three months of this year. We found that KREAM’s result is very well consistent with Liulin observation. NAIRAS is mostly higher than Liulin observation, while CARI-6M is generally lower than observation. The percent error of KREAM compared with Liulin observation is 10.95%. That is 43.38% for NAIRAS and 22.03% for CARI-6M. We found that the increase of the altitude might cause sudden increase in radiation exposure, especially for the polar route. As more comprehensive analysis is required to validate KREAM’s reliability, we plan to expand these radiation measurements with Liulin and TEPC in the near future.









