1. INTRODUCTION
CubeSat missions have become popular in the past decade, and the number of projects using CubeSats has been increasing (Han et al. 2017). These satellites have a relatively low development cost and can offer great accessibility. CubeSats have been developed for educational purposes and scientific proof-of-concept validation to enable space exploration and low-cost science missions (Tummala & Dutta 2017).
One of the major challenges in CubeSat missions is in using a propulsion system (PPS) to accomplish mission objectives (Kvell et al. 2014). Up to now, thousands of CubeSats have been developed or are under development, but only a few of these have a PPS. There have been six flight heritages regarding relative orbit control strategy for CubeSat missions that use cold gas PPSs, but only one flight heritage in the case of electric PPSs (Lemmer 2017). The realization of CubeSat orbit control may be completely different from that of large-scale satellites, depending on the requirements for orbit control. The relevant requirements include a relatively small mass, volume, and power, and limited onboard propellant (Gill et al. 2013). Nevertheless, the Space Flight Laboratory (SFL) at the University of Toronto Institute for Aerospace Studies (UTIAS) developed the Canadian Advanced Nanospace eXperiment (CanX) program, and they have successfully demonstrated the autonomous formation flying algorithm in orbit (Orr et al. 2007). For the CanX-4 and CanX-5 formation flying mission, which is part of the CanX program, the satellites were equipped with a cold gas PPS, which provides a total delta-V capability of 18 m/s (Bonin et al. 2015).
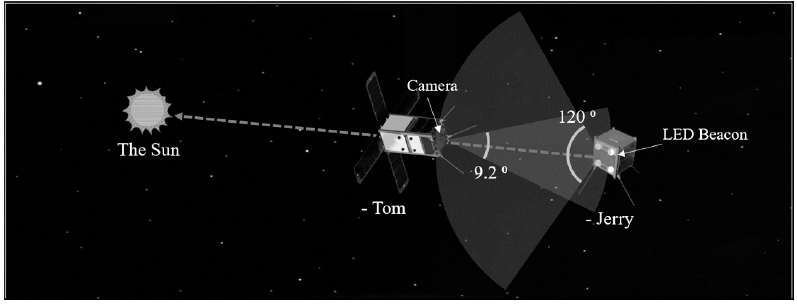
The CubeSat Astronomy by NASA and Yonsei using Virtual Telescope Alignment eXperiment (CANYVAL-X) mission, which is developed by Yonsei University in partnership with NASA Goddard Space Flight Center (GSFC), is a technical verification mission for a next-generation virtual space telescope (Park et al. 2017). To realize the virtual telescope in space, two CubeSats that function separately as optics (deputy) and detector (chief ) have to accomplish a precise formation flying, which involves arranging the CubeSats toward the same celestial object, the Sun. This process is referred to as inertial alignment. Two CubeSats nicknamed Tom (deputy) and Jerry (chief) were developed for experimenting with inertial alignment in space. On Tom, a double-size CubeSat, a low-thrust electric PPS called a micro-cathode arc thruster (mCAT), which was developed by George Washington University and tested by NASA GSFC, was installed for the orbit control. The mCAT, which has an identified maximum thrust of 50 μN, is used for reconfiguration and inertial alignment control. Both CubeSats were developed in accordance with the CubeSat Design Specification and are qualified to be operated in a space environment through environmental tests, such as thermal vacuum tests and vibration tests (Park et al. 2016). Fig. 1 shows the concept of inertial alignment. When the two CubeSats and the Sun are arranged and aligned in space, in the same manner as shown in the figure, inertial alignment is accomplished. Each CubeSat’s attitude and orbit are controlled and determined to achieve the inertial alignment. Jerry moves in natural orbit, whereas Tom’s orbit will be controlled using a thruster. On the ground, inertial alignment is considered to be achieved when Tom observes an LED beacon mounted on Jerry with a camera, and, at the same time, Tom’s deployable solar panel is toward the direction of the Sun. This alignment can be quantified as follows. The success criteria for the inertial alignment are that a relative distance within 30 m and a solar alignment error within 5° are maintained simultaneously for at least one minute. The solar alignment error refers to the included angle between Tom’s position vector and the Sun’s position in Jerry’s local vertical, local horizontal (LVLH) frame.
The two CubeSats were successfully launched on India’s Polar Satellite Launch Vehicle (PSLV-C40) from the First Launch Pad (FLP) of Satish Dhawan Space Centre (SDSC) SHAR, Sriharikota, on January 12, 2018. The mission orbit is a Sun-synchronous orbit with 500-km altitude. We received the first beacon signal on February 23, 2018, at 09:50 KST. However, although we put major effort into a ground-station communication test during the initial operation phase, we have lost the signal completely. At present, the next phase of the CANYVAL mission is under development.
This study has two objectives. The first is to develop the relative orbit control strategy based on an operation concept of the CANYVAL-X mission for meeting the requirements of an inertial alignment system. The inertial alignment system developed by NASA GSFC and this system have specific requirements: less than 30 m of relative distance between the two CubeSats and less than 1 cm/s of relative velocity. The requirements are derived from the characteristics of the hardware, including the PPS, electric power system, and vision capture system. Through the suggested orbit control strategy, the requirements of the inertial alignment system will be satisfied. Orbit control techniques discussed in literature, such as fuel-optimal reconfiguration in relative motion (Cho & Park 2009) and differential atmospheric drag control (DADC; Leonard et al. 1989), are adopted in constructing the orbit control strategy. The second is to show, via numerical simulations, the process of satisfying the requirements. The method for verifying the selected orbit control techniques and the proposed relative orbit control strategy through numerical simulations is described herein.
The rest of the paper is divided as follows. Section 2 describes the principles behind the adopted relative orbit control techniques. Section 3 discusses the simulation results, and conclusions are drawn in Section 4.
2. RELATIVE ORBIT CONTROL STRATEGY
To make Tom’s relative state satisfy the requirements of the inertial alignment system, the relative orbit control strategy is developed (Fig. 2).
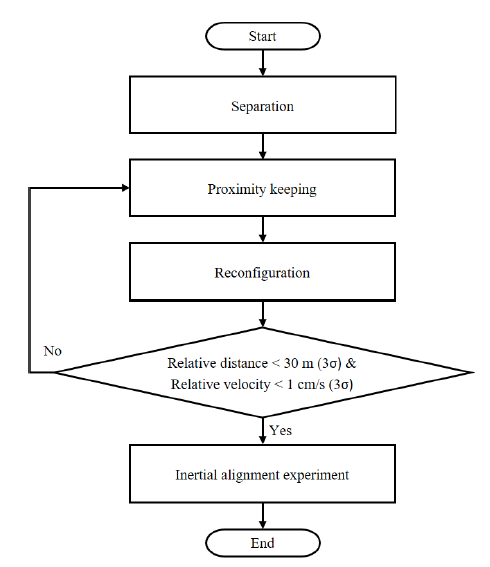
First, separation is conducted. Because separation velocity determines the configuration of the initial relative orbit, a fact that affects the orbit control efficiency, the correlation between the separation direction and the effectiveness of orbit control should be analyzed.
Second, proximity keeping comes after the separation. In the absence of orbit control, drift in the relative dynamics of the satellites occurs because of drift yielding initial conditions and perturbation forces. Thus, orbit control is essential for maintaining the relative distance at less than a few kilometers. DADC, which generates control acceleration from the differential atmospheric drag forces between two CubeSats, is applied by changing the effective cross section through attitude control and is used as a proximitykeeping technique (Leonard 1989). On-orbit performance of the technique is demonstrated by the Planet’s Flock mission, which was launched in June 2016 into a 510-km Sun-synchronous orbit (Foster et al. 2017). The feasibility of DADC for CANYVAL-X is demonstrated through simulations under various atmospheric models and atmospheric conditions.
Third, an orbit maneuver that uses a thruster to attain the requirements of the inertial alignment system is located. A reconfiguration induces Tom’s relative orbit to shrink. A general analytic solution to the fuel-optimal reconfiguration and sliding mode control (SMC) are used for the orbit controller (Cho & Park 2009). The effects of the reconfiguration are demonstrated via numerical simulations in various initial conditions. Nevertheless, because of the thrust limit and performances of the subsystems, a single reconfiguration is not enough for Tom’s relative state to satisfy the requirements of the inertial alignment system. To solve this problem, a strategy that uses multiple reconfigurations is suggested. Through the relative orbit control strategy, Tom’s relative state comes close to meeting the requirements. If it is estimated that the requirements are satisfied, the inertial alignment system is operated to conduct the inertial alignment experiment, which is the main assignment of the CANYVAL-X mission. After the experiment, Tom returns to the proximity-keeping stage and prepares for the next inertial alignment experiment.
All simulation results shown herein are discussed in Jerry’s LVLH frame because the CANYVAL-X mission focuses on the relative motions of the satellites. The definition of Jerry’s LVLH frame is as follows. The X-axis, Radial, points along the instantaneous position vector from the Earth’s center to Jerry, and the Z-axis, Cross-track, indicates the direction of satellite’s orbital angular momentum. The Y-axis, In-track, follows the right-handed rule (Z × X). Thus, In-track is toward an orbital velocity vector, but these directions are not exactly the same unless the eccentricity is zero.
This study assumes that all subsystems, such as attitude determination and control system, orbit determination system, and PPS, satisfy their respective requirements (Lee et al. 2014). We also verified this assumption through the practical development process. The specific values are listed in Table 1 (Park et al. 2016). Herein, only the orbit control is discussed.
NovAtel OEM615 GPS receiver and antenna were mounted on the CubeSats. The solutions of the GPS receiver and differential GPS algorithms are used for the absolute and relative orbit determination, respectively. A magnetometer and in-house coarse sun sensor, for attitude determination, were also mounted on each of the CubeSats. In addition, Tom has a mounted fine sun sensor, provided by NASA, and it is used to meet the system requirement during the mission.
The CubeSats, Tom and Jerry, are stuck together even after ejection from the P-POD (Poly-Picosatellite Orbital Deployer). A separation device, which is developed for the CANYVAL-X mission, is located between the two CubeSats. Tom and Jerry will remain adjoined until a separation command is issued from the ground station. In the separation device, there is a stainless-steel spring with a compressed load of 3.16 N and a spring constant of 0.23 N/mm. The separation device causes Tom and Jerry to separate gradually at a constant rate. After the separation, the relative orbit is configured. The main objective of the relative orbit control strategy is to make the values of Tom’s relative state less than the required maximum allowable values for the inertial alignment system. If the initial relative distance and velocity are excessively large, it will take considerable time to attain the requirements, and there is even a chance that the requirements will not be met. Because the relative distance and velocity are smaller, the time taken to satisfy the requirements will be shorter. Because the initial relative orbit depends on the separation velocity, we can make the initial relative orbit advantageous in the viewpoint of mission operation. The separation device uses a static spring, and the separation speed is fixed, whereas the separation direction can be changed through the application of attitude control. From the separation simulation results in Section 3.1, it is possible to know that a relatively smaller initial relative orbit can be created when the separation direction is perpendicular to the orbital plane rather than the other directions. In the satellite onboard system, the separation direction, which is the angle with respect to the orbital angular momentum vector, is determined based on the simulation result.
The relative orbit geometry can be described in terms of a set of orbit element differences relative to a common chief orbit, and thus constructing a desired relative orbit geometry analytically using element differences has been suggested (Schaub 2004). However, in the CANYVAL-X mission, drift yielding in the initial relative condition and the disparity in perturbation result from the difference in ballistic coefficient between the two CubeSats cause the relative distance not to remain at a static relative geometry. Furthermore, it is difficult to recover the relative distance if the relative distance diverges greatly. Therefore, orbit control for proximity keeping should always be on during the mission lifetime.
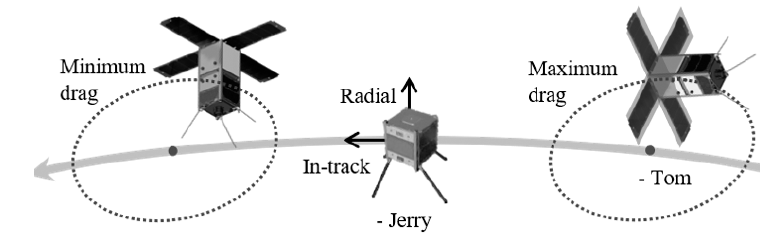
To keep the relative distance below a few kilometers, DADC, which is a proximity-keeping relative orbit control technique, is adopted (Leonard 1989). Because CubeSat missions are operated with limited resources compared with those of a normal satellite mission, proximity stating, which requires continuous orbit control, is challenging in terms of power maintenance and system stability. DADC uses the discrepancy of atmospheric drag between the two CubeSats, instead of propellant. DADC creates orbit control acceleration via differential atmospheric drag forces between the two satellites by changing the effective cross section through attitude control. The principle behind it is very simple. As a satellite suffers atmospheric drag, the total orbital energy of the satellite is decreased. When the total orbital energy is reduced, the semimajor axis becomes smaller, which means that the satellite attains a faster orbital speed. The amount of energy loss of the deputy can then be controlled by controlling its attitude. As a result of this sequence, the relative distance between the satellites is maintained within a distance criterion for mission objectives. Because the CANYVAL-X mission is a low Earth orbit mission with about 500-km altitude, it can be assumed that the atmospheric drag will have a great deal of impact on Tom and Jerry. The control strategy for DADC is shown in Fig. 3. If the center of Tom’s relative orbit is located in the positive along-track direction, Tom’s attitude is controlled to have a minimum effective cross section with respect to the atmosphere. In the opposite direction, Tom’s attitude is controlled to have a maximum effective cross section. In this way, the lengthening of the relative distance between Tom and Jerry is prevented, and maintaining the formation can be achieved.
The control acceleration from differential atmospheric drag is described using Eq. (1); ¨y is the control acceleration in the in-track direction on Jerry’s LVLH frame, CD is the drag coefficient, υrel is the orbital velocity with respect to atmosphere, ρ is the atmospheric density, A is the effective cross-sectional area of the CubeSat, and m is the mass of the CubeSat. If Tom’s attitude is controlled to have a maximum effective cross-section, ¨y will be a positive value, and if Tom’s attitude is controlled to have a minimum effective cross-section, ¨y will be a negative value, and Tom’s relative orbit will move gradually negative in the in-track direction. In this study, we used the properties of the CubeSats (Table 2) in numerical simulations. Ballistic coefficient refers to how sensitive the satellite’s motion is to the atmosphere. Whether Tom’s ballistic coefficient is bigger than that of Jerry or not depends on Tom’s attitude. DADC uses this property.

|
There are many advantages of using DADC as the controller for the proximity keeping. Because of the lack of a conventional PPS, the system can save on mass, and there is no contamination from the propellant exhaust. There is no shock or vibration because of the relatively minute acceleration. However, there are also drawbacks. First, because DADC can control only the along-track drift of the deputy’s trajectory, controlling the cross-track drift becomes difficult. Furthermore, it cannot control positions to a high accuracy in a short time (Leonard 1989). Mathematical modeling of the motion is also difficult because of numerous unpredictable time-varying factors in atmospheric models (Kumar et al. 2007).
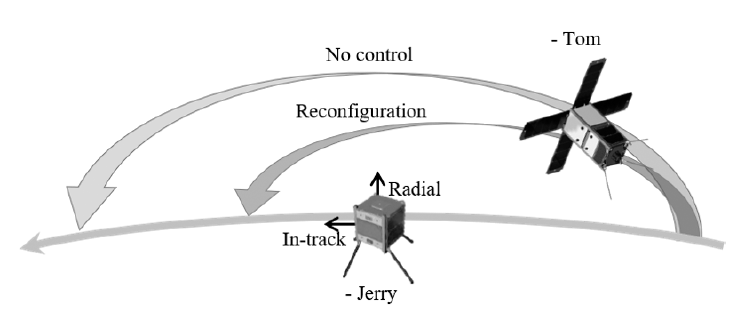
The relative distance will be maintained within a few kilometers through the DADC, but Tom’s relative state cannot meet the requirements of the inertial alignment system, which are given as a relative distance of less than 30 m between the two CubeSats and a relative velocity of less than 1 cm/s, without orbit maneuver. In general, reconfiguration refers to the orbit maneuver of a satellite to a desired state using thrusters, whereas in the CANYVAL-X mission, reconfiguration refers to reducing the relative distance and velocity of the deputy. The reconfiguration strategy is shown in Fig. 4. The desired final state is derived from determined values of how much the relative distance and velocity should be reduced, based on the final state of natural trajectory. The percentage reduction is set 10% upon consideration of the PPS and electric power system. In addition, because of the capacity of the electric power system, the orbit maneuver lasts for half an orbital period. Eventually, the reconfiguration is sustained for half a period, which makes Tom’s relative state to be 90% of the final state of natural trajectory. For the efficiency of the orbit maneuver, when it is determined on the on-board computer that the relative position of Tom is located at the opposite side of Jerry’s LVLH frame after half a period, the satellite system operates the reconfiguration. This restriction is needed for accomplishing the purpose of reconfiguration, which is the reduction of the relative distance and relative velocity.
A control method adopted in reconfiguration is an analytic solution for fuel-optimal control in relative motion (Cho & Park 2009), which minimizes the total amount of fuel during the trajectory. To find the optimal trajectory and thrust at each step, the theory of calculus of variations is used, and then Hill’s equations, which are linearized equations presenting the relative motions for near-circular orbit, are applied in the general form of the analytic solutions. In their approach, if the basic feature of the state equations is satisfied, the calculation of the inverse of the fundamental matrix associated with dynamic equations is not required. Therefore, this method has advantages in terms of reduction in calculation load. This approach has low computational complexity because the inverse of the fundamental matrix is obtained in advance through a single calculation. Considering the computing power of a CubeSat’s on-board computer, and a real-time orbit control scenario, a simple form for the control algorithm is necessary. Furthermore, predicting the explicit form of optimal solutions throughout the reconfiguration is possible because the dynamic equations are given in advance. Not only the controlled state solutions but also the optimal thrust vector can be expressed concisely as a function of the fundamental matrix of the given state equations, and the state vector during the reconfiguration. However, this method has weak point in that because it uses Hill’s equation, which expresses the relative dynamics of the satellites in the simplest way, its modeling is imperfect. SMC deals not only with the imperfection in modeling but also with disturbances. SMC can provide robustness in the control, maintaining stability, and consistent performance (Liu et al. 2006). Furthermore, it uses Lyapunov stability theory, wherein stability is guaranteed. The general analytic solutions to the fuel-optimal reconfiguration plays a desired role in the trajectory in the tracking control of the SMC. Details on the controller are described in the reference (Lee 2018).
Nonetheless, the requirements of the inertial alignment system cannot be satisfied with a single reconfiguration because of the thrust limit and electric power supplement issue. Thus, a proposed solution to this problem is the use of multiple reconfigurations over several days. As indicated in the flowchart (Fig. 2), the orbit control sequence is repeated until the requirements of the inertial alignment system are satisfied. Tom and Jerry maintain a few kilometers of relative distance during the proximity-keeping mode through the DADC. The reconfiguration control is performed to meet the requirements of the inertial alignment system. If Tom’s relative state is judged to be satisfying the requirements of the inertial alignment system, the satellite system starts the inertial alignment experiment; otherwise, the system performs re-entry to the proximity-keeping mode or powercharging mode and prepares for the next reconfiguration. Simulations of the multiple reconfigurations are conducted to determine the validity of this strategy. Prior to the simulations, an assumption is established, which is that the next reconfiguration is performed immediately after the previous orbit control. After a single reconfiguration, a power charging stage is necessary, so that the relative distance between the two CubeSats can be disturbed during the absence of orbit control. However, the assumption is made because it has been determined that similar relative states after the reconfigurations can be obtained again through the proximity-stating mode. Therefore, the multiple reconfigurations are executed continuously under this assumption.
A low-thrust electric PPS called a mCAT, which was developed by George Washington University and tested by NASA GSFC (Keidar 2015), is installed in Tom for the orbit maneuver. The thruster magnitude was designed to be 200 μN in the early stages of development; however, in the final thrust test, it was identified to be 50 μN. It is confirmed that the mission has a possibility of success with a 50-μN thrust, even though using a large thrust would be more advantageous to accomplishing the objectives of the mission.
The inertial alignment system is developed for performing the inertial alignment experiment, which would demonstrate an essential technique for nextgeneration virtual space telescopes. The control algorithm was developed by NASA GSFC. It controls the relative orbit and attitude simultaneously and allows CubeSats to align toward the same object, the Sun. The system comprises a combination of several subsystems, such as the Guidance, Navigation, and Control system (GNC), Attitude Determination, and Control System (ADCS), PPS, and Inter- Satellite Link system (ISL) (Park 2017). If Tom’s relative state satisfies the requirement of having a relative distance of 30 m or less and a relative velocity of 1 cm/s or less, the satellite system operates the inertial alignment system. The success criterion for inertial alignment is that the relative distance is maintained within 30 m (3σ), and the solar alignment error is maintained within 5° (3σ), concurrently for one minute. The relative distance requirement is derived from the performance of the vision capture system. The solar alignment error refers to an angle between Tom’s position vector and the Sun’s position in Jerry’s LVLH frame. In simulations of the inertial alignment experiment, if the inertial alignment among the CubeSats and the Sun is configured depending on those criteria, the main mission of CANYVAL-X is said to be a success.
The PPS equipped in Tom (mCAT) can thrust in only one direction, and therefore the turn-and-burn mechanism, which utilizes a three-axis attitude control system and the PPS, is adopted accordingly. Three-axis attitude control turns the satellite and induces the thruster nozzle to be aligned in the direction of the thrust vector, which is calculated from the orbit control algorithms. The thruster then fires. Details on the controller are described in the reference (Lee 2018).
3. SIMULATION RESULTS AND ANALYSIS
In this section, simulation results for the relative orbit control methods proposed in the previous sections are presented. Note that we have verified that the subsystem requirements, such as attitude determination and control, relative orbit determination, and PPS, are satisfied through the mission development process. Therefore, in this paper, only orbit control is described and examined under the assumption. Furthermore, all simulation results are expressed in Jerry’s LVLH frame. Initial orbital elements for numerical simulations are as follows. The semi-major axis is 6,878.334 km, eccentricity is 0.0012, inclination is 97.653°, right ascension of ascending node is 74.0619°, argument of perigee is 201.489°, and epoch is 2018.01.12 04:20:38.880 (UTC).
The self-developed separating device located between the two CubeSats induces the separation. The device causes Tom and Jerry to separate gradually at constant speeds: 7 cm/s for Tom, and 20 cm/s for Jerry. The separation speed is based on the center of mass of the combined Tom-and- Jerry system. In other words, the relative separation speed is 21 cm/s. These values are obtained from the mechanical dynamic simulation of the separation device. Whereas the separation speed is fixed, the separation direction determining the initial relative orbit configuration is changeable because of the attitude control system. The correlations between the separation direction and the initial relative orbits are presented in Fig. 5. Each angle listed in the legend of graph refers to the measure of the angle between the orbital plane and separation vector. If Tom and Jerry are separated in the horizontal direction with respect to Jerry’s orbital plane, the maximum relative distance reaches about 980 m and relative speed about 0.54 m/s. On the other hand, if the angle is close to 90°, then the maximum relative distance is only about 250 m and the maximum relative velocity about 0.27 m/s for one orbital period after the separation. These values demonstrate that the initial relative orbit can be smaller if the separation direction is perpendicular to the orbital plane. However, regardless of angles, the relative distances between Tom and Jerry become zero after one orbital period. The effectiveness of relative orbit control is influenced more by relative velocity than by relative distance. In other words, the orbit control can be more effective in terms of fuel consumption and feasibility when the initial condition of the orbit control is set with a minimum relative velocity rather than a zero initial relative distance.
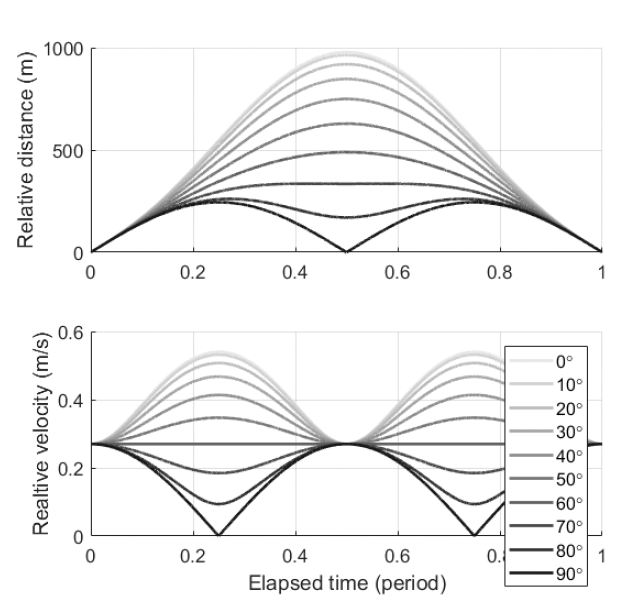
Fig. 6 shows the reason why the vertical separation with respect to the orbital plane is determined. Meanwhile, for the horizontal separation with respect to the orbital plane, the relative distance is kept within 1 km, and the distance after the vertical separation is maintained within a few hundred meters. Because it is more advantageous to control the relative orbit when the magnitudes of the relative distance and velocity are relatively small, this result implies that vertical separation is more advantageous in terms of orbit control. Similar advantages in the same respect can be seen in the reconfiguration simulation result. The percentage of distance reduction after reconfiguration with an initial condition starting from horizontal separation is 6.293%, and that in the case of vertical separation is 14.24%. Furthermore, when simulation begins with horizontal separation, multiple reconfigurations are required seven times to arrive at the requirement of the inertial alignment system, whereas with vertical separation, multiple reconfigurations are needed only five times (Lee 2018).
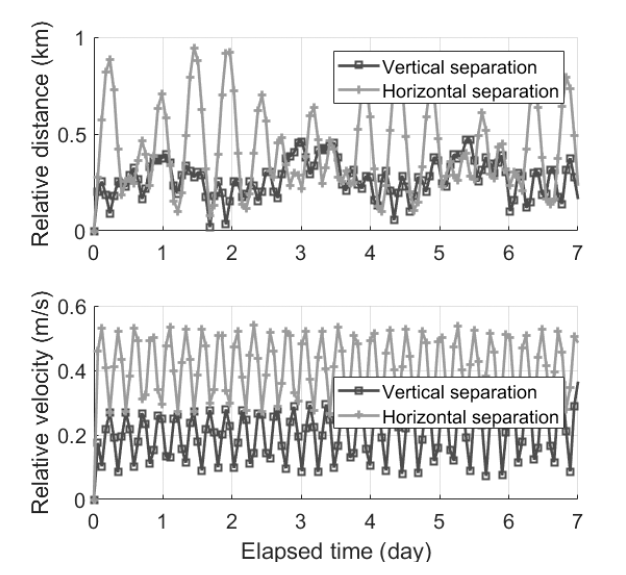
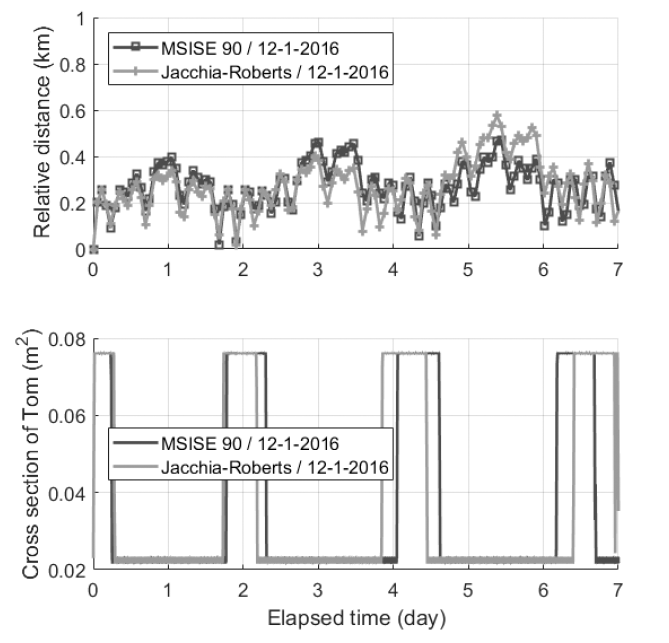
The DADC, which utilizes atmospheric density, is used for proximity keeping. Because this technique uses atmospheric density, it is important to understand the correlation between the atmospheric density and the control performance. Fig. 7 shows how relative trajectory is affected by atmospheric models and atmospheric density variation when two CubeSats are propagated for just one week. These trends indicate that if the discrepancy of drag acceleration has a positive value, then the trajectory of the deputy (Tom) will go forward with respect to the chief (Jerry). This property can be calculated from Eq. (1). The top subfigure of Fig. 7 illustrates the relative distance, and the bottom subfigure visualizes the drift component of Tom’s relative trajectory. The graph shows that the difference between the two atmospheric models, MSISE-90 and Jacchia- Roberts, is not significant. By contrast, the atmospheric conditions according to the date greatly affect the dynamics of the satellites. Space weather data can be downloaded from Celestrak (http://www.celestrak.com/). In the case of simulation using space weather data from December 1, 2016, the relative distance between Jerry and Tom becomes about 200 km. For December 1, 2012, the relative distance is approximately 70 km. Similar results are derived from the drift component graph. The effects of date are more influential than the effects of a specific atmospheric model on the satellite’s relative motion. According to the data for the respective years, both geomagnetic activity and solar activity are more energetic in 2012 compared with those in 2016. These energetic environments result in a higher atmospheric density, which will have a greater impact on the satellite motion.
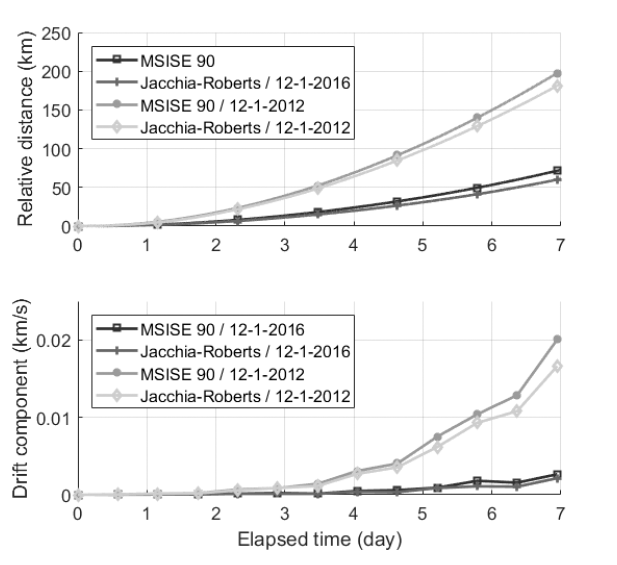
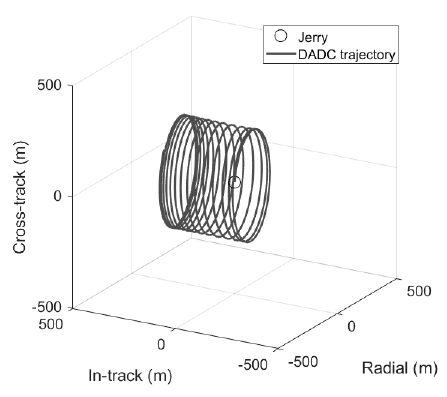
Fig. 8 illustrates the simulation results of DADC using space weather data from December 1, 2016. There is no noteworthy difference between simulation results using MSISE-90 and those using Jacchia-Roberts. The top subfigure shows that the relative distance is maintained within few hundred meters, which means the DADC can be a relative orbital control method for the proximity-keeping mode in the CANYVAL-X mission. The bottom graph illustrates the effective cross section of Tom. Attitude control changes the effective cross section from minimum to maximum or vice versa. The fact that attitude control takes about 1,000 s is reflected in the numerical simulations. For the maximum or minimum effective cross-sectional area to be maintained, it is necessary to keep the same attitude with respect to the atmosphere, and thus attitude control should be continuously performed. The reason why the sections for the minimum effective cross-sectional area are bigger than the sections for the maximum effective cross-sectional area is that the discrepancy of atmospheric drag between Jerry and Tom is bigger when Tom has the maximum area than when Tom has the minimum area. It is possible to execute proximity keeping via attitude control once a day. The relative trajectory on proximity staging will have the shape of a lying spring (Fig. 7). Tom hovers around Jerry, configuring the shape of a coil while DADC is ongoing (Fig. 9).
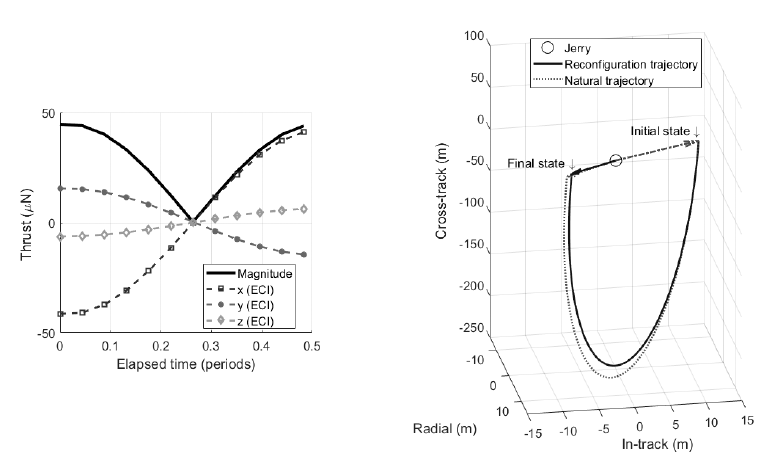
The reconfiguration is conducted to reduce the relative distance and velocity of the deputy (Tom). As proposed in the reconfiguration strategy (Section 2.3), the desired final relative state of Tom after the half orbital period is decided to be 90% of the final state of the natural trajectory. Fig. 10 represents a simulation of the reconfiguration. The left subfigure illustrates the thrust expressed in the inertial frame, which is applied in the dynamics of Tom. The thrust magnitude is below 50 μN while the orbit control is performed. The right subfigure is a three-dimensional plot of Tom’s relative trajectory. The final relative distance and speed of the natural trajectory are 22.90 m and 27.09 cm/s, respectively, the desired final relative distance and speed are 20.61 m and 24.38 cm/s, respectively, and the final relative distance and speed of the controlled trajectory are 19.28 m and 24.39 cm/s, respectively. Through the reconfiguration, the relative distance and velocity are reduced by about 3.62 m and 2.7 cm/s, respectively, and this result corresponds with that of the reconfiguration reducing the final state of the natural trajectory by 10%. Furthermore, in the previous section, the vertical separation with respect to the orbital plane was chosen to configure the smaller initial relative orbit for enabling efficient orbit control. Fig. 10 shows that this concept also has validity in the reconfiguration phase. Because the vertical velocity component is stronger than the horizontal, a vertical relative trajectory is formed.
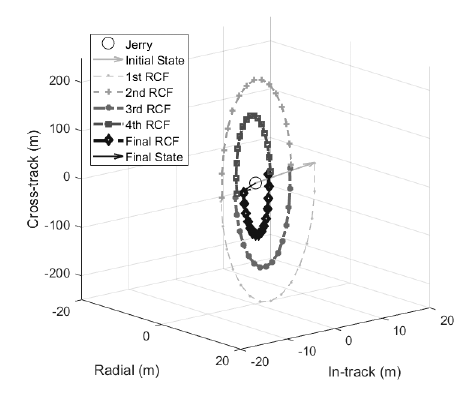
As already mentioned, the relative orbit control strategy comprises a repeated proximity-keeping and reconfiguration sequence because a single reconfiguration is not enough to make Tom’s relative state satisfy the requirements of the inertial alignment system. Fig. 11 represents the simulation result of multiple reconfigurations. In the figure, the size of the relative trajectory decreases gradually as the reconfiguration is repeated. The final relative distance and speed of the simulation of multiple reconfigurations are 11.86 m and 10.71 cm/s, respectively, after five reconfigurations, and these values satisfy the requirements of the inertial alignment system. These values will be used in the simulations of the inertial alignment experiment as an initial condition.
As a result, the number of reconfigurations in the multiple- reconfiguration stage may be reduced. This inference is confirmed by numerical simulations.
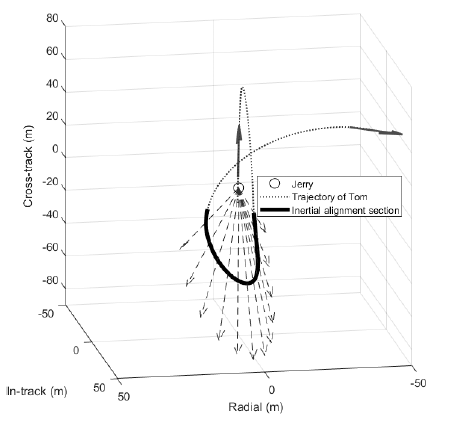
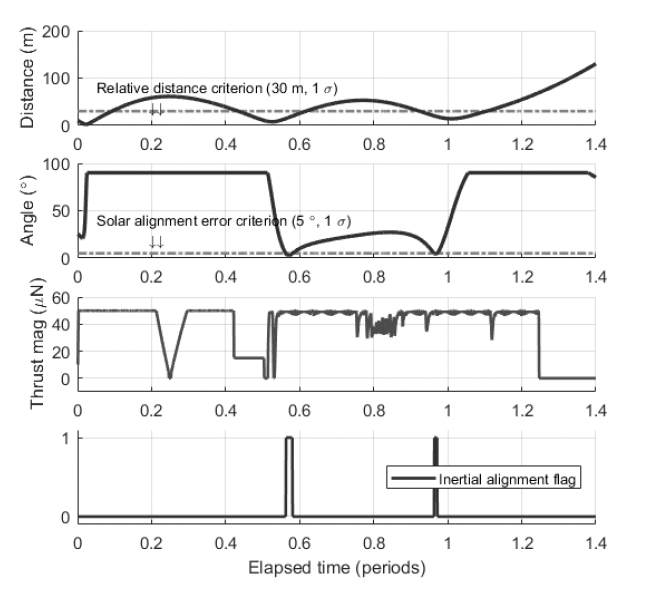
The inertial alignment experiment is the final stage of the relative orbit control strategy, and it is also the final goal of the CANYVAL-X mission. Tom’s relative state after the multiple reconfiguration is used as the initial condition for the simulation of the inertial alignment experiment. Fig. 12 and Fig. 13 cover the simulation results. Fig. 12 shows the numerical result of the simulation, and Fig. 13 illustrates the three-dimensional plot of Tom’s trajectory with respect to Jerry during the inertial alignment experiment. In the first and second row of Fig. 12, dashed lines represent the success criteria for inertial alignment, wherein the relative distance is within 30 m, and the solar alignment error is within 5°. The inertial alignment is said to be achieved only when these two conditions are considered at once, and these conditions should last for at least 1 min. In this experiment, the resulting alignment duration time is about 145 s, which satisfies the success criteria for the inertial alignment, and the flag is raised when both criteria are satisfied at the same time. The total amount of impulse used in the inertial alignment experiment is 0.3107 Ns. In Fig. 13, Tom maneuvers to the vicinity of Jerry, and inertial alignment is fulfilled through the synchronized motion of the position vector of Tom and those of the Sun, as illustrated by the solid arrows oriented from Jerry. These simulation results suggest that the inertial alignment experiment, which is the main mission of CANYVAL-X, can be performed through the proposed relative orbit control strategy.
4. CONCLUSIONS
The main goal of the CANYVAL-X mission is to demonstrate an essential technique for the next-generation virtual space telescope. Two CubeSats, Tom (deputy) and Jerry (chief ), that function separately as optics satellite and detector satellite, respectively, are designed and developed for the CANYVAL-X mission. The core technology for realizing the virtual space telescope is the inertial alignment system, which controls the two CubeSats’ attitudes and Tom’s relative orbit simultaneously. To accomplish the inertial alignment, the requirements of the inertial alignment system, which are that the relative distance between the two CubeSats is 30 m or less, and that the relative velocity is 1 cm/s or less, should be satisfied.
The relative orbit control strategy, which comprises separation, proximity, and reconfiguration, is developed to make the relative state of Tom fulfil the requirements. From the separation analysis, it is revealed that vertical separation between the combined CubeSats with respect to the orbital plane, which produces a smaller initial relative orbit, is more advantageous in terms of orbit control. After the separation, two CubeSats start the proximity keeping via DADC. The simulation results show that the relative distance can be maintained within a kilometer, and it is confirmed that proximity keeping via DADC is working.
Before the inertial alignment, Tom conducts an orbit maneuver to reduce the relative distance and velocity. A lowthrust electric PPS called a mCAT, which was developed by George Washington University and tested by NASA GSFC (Keidar 2015), is installed in Tom for the orbit maneuver. However, because it is difficult to make the relative state of Tom satisfy the requirements with a single reconfiguration, reconfigurations are performed until Tom is close enough to reach Jerry. The simulation result of the multiple reconfiguration shows that the relative state of Tom can meet the requirements. If the satellite is in on-orbit operation, about one week would be consumed to satisfy the requirements because at least one day is needed for one reconfiguration.
The relative state of Tom obtained from the relative orbit control strategy is applied to the inertial alignment experiment simulation. The simulation result verifies that the inertial alignment can be realized by satisfying the success criteria. The simulation results in this paper specify that the inertial alignment, which is an essential technique for the virtual space telescope, can be achieved through the proposed relative orbit control strategy. Furthermore, if the strategy and PPS of the CANYVAL-X mission were successfully demonstrated, it would increase the applicability of these technologies to extensive space missions and enhance the capabilities of future CubeSat missions.










