1. INTRODUCTION
Due to many scientific reasons, including the potential of mining resources, interest regarding Moon missions is increasing again. Recently, the National Aeronautics and Space Administration (NASA) have announced a plan to land the first female astronaut on the Moon in 2024. It also aims to establish a sustainable human presence on the Moon by 2028 (NASA 2019). In line with these trends, Korea is now beginning to expand its interests to planetary exploration. Korea began preparing for a lunar exploration mission in 2013 with plans to launch the first experimental lunar orbiter, the Korea Pathfinder Lunar Orbiter (KPLO), before the end of 2020. After completing the KPLO mission, future missions will focus on lunar surface investigations using landers and rovers (Song et al. 2018). For the successful flight operation of the KPLO, considerable relevant works have been performed focused on: trajectory design (Choi et al. 2016, 2018), error and contingency analysis (Bae et al. 2016a, b;Bae et al. 2017a, b, c;Song et al. 2017a), flight dynamics subsystem development (Lee et al. 2017;Kim et al. 2017a;Song et al. 2016;2017b), and navigation analysis (Kim et al. 2016a, b;Kim et al. 2017b, c, d, e; Kim et al. 2018a, b, c;Kim et al. 2019), among others.
Another interesting trend in current planetary exploration is the application of CubeSats. Enhanced miniaturization technologies have led to more demanding proposals for CubeSat missions beyond low Earth orbit, including exploration of the Moon and far beyond the solar system. The Mars Cube One (MarCO), the first interplanetary CubeSat, successfully demonstrated that a CubeSat can operate, communicate, and navigate far from Earth (JPL 2019). Actually, several planetary CubeSat missions have already been proposed and scheduled for launch in the near future, including: the Interplanetary NanoSpacecraft Pathfinder In Relevant Environment (INSPIRE) (Klesh et al. 2013), the Deep Interior Scanning CubeSat (DISCUS) (Bambach et al. 2018), and DustCube, which is part of the Asteroid Impact Mission (AIM) (Perez et al. 2018). Moreover, thirteen CubeSats (CuSP, LunaH-Map, Lunar Flashlight, Lunar IceCube, NEAScout, LunIR, EQUULEUS, OMOTENASHI, ArgoMoon, Cislunar Explorer A, B, CU-E3, and Miles) will travel into deep space aboard the maiden flight of the Space Launch System as a secondary payload (Alkalai 2018).
Regardless of the size of the spacecraft, station-keeping (SK) maneuvers to maintain the mission orbit within the deadband limits are essential, not only for unique scientific studies, but also for good-quality scientific data. Moreover, the required delta-V for SK maneuvers should be estimated and analyzed during the mission design phase, as the allocated propellant masses for SK maneuvers are critical to the overall mission lifetime. In fact, KPLO is designed to fly at an altitude of 100 km with a ±30 km deadband limit (Song et al. 2018), and the Lunar Reconnaissance Orbiter (LRO) maintained its orbit nominally at an altitude of 50 km with a ±20 km deadband during primary science operation (Mesarch et al. 2010) to maximize its scientific returns. The Lunar Prospector (LP) and KAGUYA mission flew with a 100-km altitude for a nominal mission with ±20 km (Lozier et al. 1998) and ±30 km (Sasaki et al. 2003) deadband limits, respectively. As SK maneuvers are closely related to the overall mission lifetime, numerous studies have been extensively performed to reduce the allocated fuel masses for SK maneuvers. Further, the fuel cost of SK maneuvers could be reduced by adapting different SK maneuver operation strategies, or the mission orbit could be changed to a frozen or quasi-frozen orbit of the Moon. In addition, performing a mission around the lunar liberation point could be another solution to reduce the overall fuel cost. Further details can be found in the literatures, as there exist many relevant references.
Although the SK maneuver fuel cost could be reduced with the methods discussed, it can only be achieved with limited orbital conditions, such as limited altitudes, eccentricities, and inclinations, among others. Moreover, payloads should be designed and developed to guarantee performance under such limited orbital conditions, and should certainly be the major driving factor while the overall mission concept is being established. Such a mission could be relatively easily planned, designed, and achieved with a large-size spacecraft, however, the limited orbital conditions would seriously diminish CubeSat applicability to planetary missions. To maximize the major benefits of CubeSat class application to planetary missions, a high return-to-cost ratio should be guaranteed, to not only reduce the complexity in terms of system development, but also of operations. One alternative way to maximize the benefit of utilizing CubeSats that have formulaic platforms would be to lower the mission orbit as much as possible and apply a classical SK maneuver strategy with a typical mission orbit, i.e., a circular orbit with consistent deadband limits. Flying at an extremely low altitude could return high-resolution images without major changes to the miniaturized camera already developed for the CubeSat platform. Furthermore, other meaningful scientific data, such as the magnetic field near the lunar surface, could be measured by flying at an extremely low altitude. Applying a simple SK maneuver strategy would also result in a simple and reliable operation concept, which is a more preferable choice for CubeSat application.
The main focus of the current work is to perform an early phase feasibility analysis of a CubeSat mission, particularly flying at an extremely low altitude on the Moon. Firstly, using a high-fidelity force model, the required SK maneuver delta-Vs for maintaining an extremely low lunar altitude are obtained. Based on the derived overall SK maneuver delta- Vs cost, the possibilities of performing a CubeSat mission are analyzed by applying the current flight-proven miniaturized propulsion system performances. The remainder of this manuscript is organized as follows: A detailed targeting problem formulation using System Tool Kit (STK) Astrogator to maintain the nominal altitude, with given deadband limits, is explained in Section 2. The numerical implications and assumptions adopted in the current work are discussed in Section 3, using the high-fidelity force model setting. Then, the simulation results focusing on the SK delta-V requirement with respect to different reference orbits are analyzed in Section 4, with an analysis of CubeSat mission feasibilities. Finally, the conclusions are presented in Section 5.
2. TARGETING PROBLEM FORMULATION FOR STATION-KEEPING MANEUVER
The spacecraft flying vicinity of a central body usually experiences perturbing forces due to the nonlinear gravitational field of the central body along with third bodies. Therefore, orbital motions gradually change with time, and the SK problem can be summarized to formulate the problem of maintaining the reference orbital altitude href by perturbing the orbit using maneuvers Δv within a specified set of goals Δh, namely, the deadband limits. To formulate and target the SK problem, current work has utilized STK Astrogator by Analytical Graphics Inc. (AGI) with the high-fidelity force model. Astrogator is an add-in module of the STK that enables the user to design a Mission Control Sequence (MCS) to model the launch, maneuvers, and trajectory targeting parameters (Carrico & Fletcher 2003). Actually, Astrogator is the third and most recent version of a program originally developed by the NASA Goddard Space Flight Center and has been used to design and operate many missions, including Earth and non-Earth missions, such as Clementine, Wind, SOHO, ACE, LP, MAP, LRO, and LADEE, among others (Carrico & Fletcher 2003).
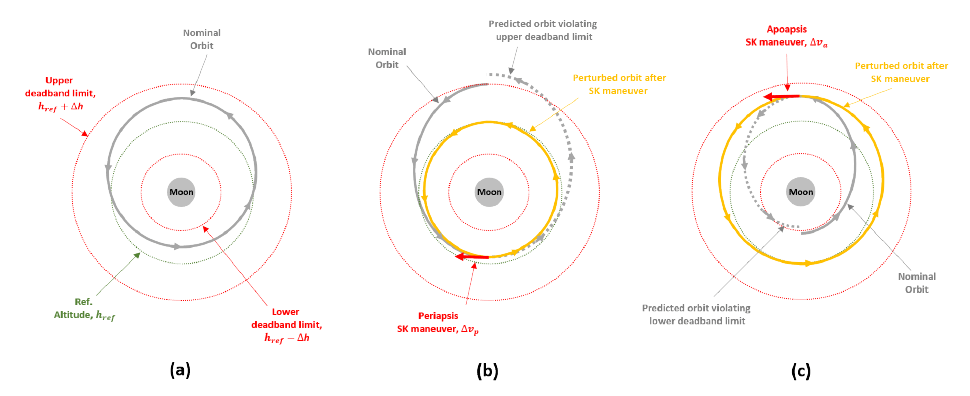
Maintaining href within ±Δh at a lunar orbit can be achieved by performing a series of periapsis and apoapsis maneuvers during the predefined mission lifetime tf. The applied delta-V at the periapsis Δvp usually aims to adjust the next upcoming first apoapsis altitude . Similarly, the delta-V induced at the apoapsis Δva will adjust the next upcoming first periapsis altitude , where the subscripts a and p denote the apoapsis and periapsis, respectively, and the superscript n denotes the next upcoming first event. In Fig. 1, the basic geometry of SK maneuvers to maintain the reference altitude is shown. Fig. 1(a) shows a nominal case in which the spacecraft orbit lies within the boundaries of both the lower and upper deadband limits. An upper deadband limit violation case is shown in Fig. 1(b), for which the adjust maneuver Δvp will occur at the periapsis passage time tp. Finally, an example of a lower deadband limit violation case is depicted in Fig. 1(c). Like the upper deadband limit violation case, the adjust maneuver Δva will occur at the apoapsis passage time ta for this case.
To solve the given SK problem, as previously described, an MCS was established using the Astrogator module with several target sequence segments nested. The target sequence provides Astrogator with a powerful capability to solve very complex space flight dynamics by defining the maneuver and propagation components inside to achieve the final design goals. With high-fidelity force models (the detailed setup of which will be explained in the following subsection), three different OR logical stopping conditions were given to trigger the following sequential event inside the MCS.
In Eq. (1), the stopping condition of ha is derived based on the constraint of at . If the predicted is less than the lower deadband limit (), then the periapsis raising sequence is triggered. To raise , another target sequence was constructed inside the MCS by simply imparting Δva at ta as follows:
where va is the velocity of the CubeSat at the apoapsis and v is that just after a maneuver. Here, Δva is given as a control variable to meet the equality condition of = href at . Another stopping condition hp was derived in a similar way to that of ha. The stopping condition of hp is triggered based on the constraint of at . If violates the upper deadband limit condition (), then the apoapsis altitude is lowered by imparting Δvp at tp : v = vp + Δvp, and Δvp is given as a control variable to meet the equality condition of . Finally, the overall MCS will be terminated if the stopping condition of tf is satisfied, as the predefined mission lifetime is reached. Fig. 2 shows the overall MCS workflow diagram for the current targeting problem, as discussed.
3. SIMULATION SETUP AND ASSUMPTIONS
The simulation of the current work began from the assumption that a CubeSat is inserted into the reference orbit and starts its nominal mission at 1 January 2025 00:00:00.000 UTC. Indeed, CubeSat may consume additional fuel to achieve its final mission orbit, the reference orbit. However, current work has not considered the fuel costs required for mission orbit insertion phases, as fuel costs for these phases may be strongly dependent and changeable to the overall mission orbit insertion strategy. The reference orbit was selected as a circular polar orbit around the Moon, namely of 90° inclination with zero eccentricity, having four different reference altitudes above the mean lunar surface; 20, 30, 40, and 50 km. The remaining orbital elements, i.e., the right ascension of ascending node, argument of the periapsis, and the true anomaly, were all set to zero. For each reference orbit, two different deadband sets (±5 and ±10 km) were considered; therefore, a total of 8 different reference orbit sets were considered for the simulation. With given initial states, the CubeSat aims to perform a mission during one month, maintaining the dedicated reference orbit, or, more specifically, the mission lifetime was given as one month. To propagate the reference orbits, a highprecision orbit propagator was newly configured using Astrogator with a numerical integrator setup, as shown in Table 1. A detailed description of the parameter settings is shown in Table 1, as can be discovered through the AGI support system (AGI 2019).

|
To solve the targeting problem formulated in Section 2, a well-known differential corrector algorithm with singular value decomposition was applied, which is a robust mechanism used by Astrogator. Within this algorithm, the maximum iteration limit for a single run was set as 100, with convergence criteria of the equality conditions within the tolerance. For root-finding, the Secant method was applied with the forward difference derivative calculation method. Finally, all maneuvers were assumed to be impulsive maneuvers to maintain the reference orbit within the deadband limit, and only the velocity component of the maneuver was controlled among the three components of the maneuver expressed in the velocity-normal-conormal (VNC) reference frame, as to focus on a preliminary analysis. In the VNC frame, it should be noted that the unit x-axis is defined as along the velocity vector, the unit y-axis is along the orbit normal, and the unit z-axis completes the orthogonal triad.
4. RESULTS AND DISCUSSIONS
Before the SK characteristics can be discussed with respect to the different lunar altitudes having different deadbands, the importance of the selection of appropriate degree and order of lunar gravitational harmonics must be discussed. As the current work considered very low altitude ranges on the Moon, the resultant orbits may be considerably affected by the nonspherical harmonics of the Moon. Among the eight different sets of candidate reference orbits, the lowest reference altitude condition was selected and analyzed for the effects of the different degree and order of nonspherical harmonics of the Moon on the SK strategy.
Table 2 summarizes the characteristics of the SK maneuvers under the three different sets of the degree and order of nonspherical harmonics (300 by 300, 450 by 450, and 660 by 660), with the reference orbit having a 20- km altitude with a ±10 km deadband. As is clearly shown in Table 2, considering the 300 by 300 degree and order would not be sufficient to derive accurate SK maneuver characteristics as it can lead to different numbers of maneuvers during the predicted 1-month timespan; therefore, the magnitude of the total delta-V would also be inaccurate. At least the 450 by 450 degree and order should be considered to derive a meaningful SK maneuver under 20-km altitude with ±10 km deadband conditions. However, it should be noted that considering 450 by 450 could still lead to a slight difference in the total delta-V magnitude, with a different execution time compared to the full degree and order of 660 by 660. These phenomena are due to the inaccurate acceleration accumulation, mainly induced from insufficient consideration of the degree and order of nonspherical harmonics. The lunar apoapsis and periapsis altitude variation history is depicted in Fig. 3 for each of the cases. In Fig. 3, the x-axis is the elapsed time since the epoch and the y-axis denotes the corresponding altitude variations due to the SK maneuvers. Fig. 3(a) displays the case when 300 by 300 degree and order of nonspherical harmonics is considered, while Fig. 3(b) is for 450 by 450, and Fig. 3(c) for 660 by 660. Additionally, every sharp peak in Fig 3 denotes the point where the periapsis or apoapsis altitude-adjusted SK maneuver is executed.

|
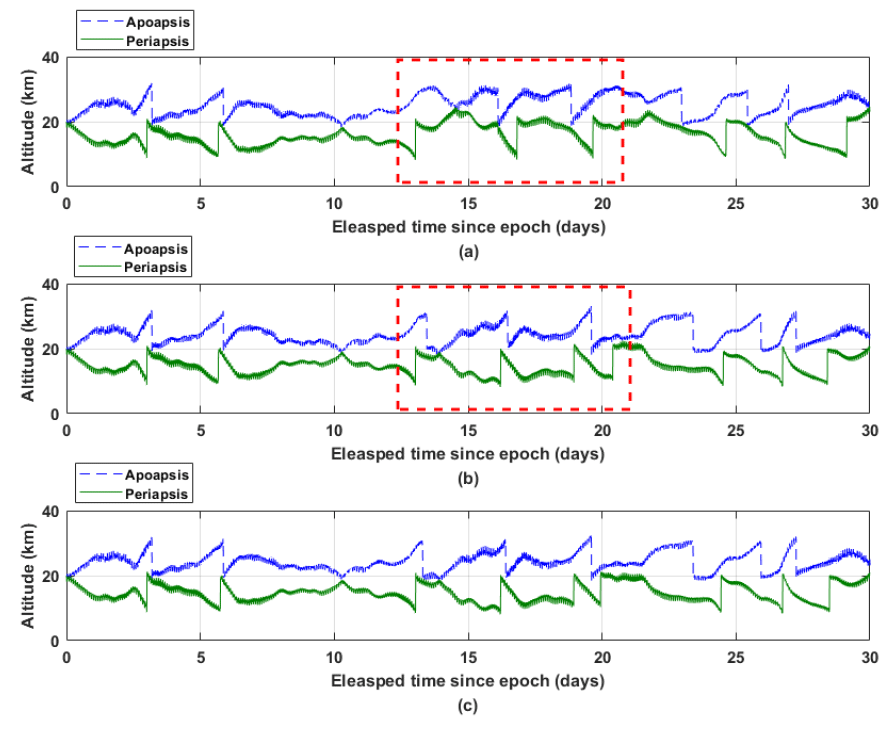
From Fig. 3, the behaviors of the periapsis and apoapsis altitude variations remain similar until approximately 12.5 days since the epoch. However, from 12.5 days until approximately 21 days, both the periapsis and apoapsis altitudes vary completely differently (see boxes in Fig. 3 marked with dotted red line) between Figs. 3(a) and 3(b). It is clear that the selection of different degree and order of nonspherical harmonics causes the difference in the orbit propagation performance, and results in entirely different SK maneuver strategies. A total of 5 SK maneuvers (3 maneuvers executed at the periapsis and 2 at the apoapsis) were expected when the 300 by 300 degree and order of non-spherical harmonics was applied for the timespan from 12.5–21 days; however, if 450 by 450 is applied, then the total number of SK maneuvers will increase to seven: four maneuvers executed at the periapsis and three at the apoapsis of the orbit. Unlike the variation trend between Figs. 3(a) and 3(b), the overall variation behaviors between Figs. 3(b) and 3(c) are very similar, except the difference in the SK maneuver execution times. Although the results with the degree and order of 450 by 450 nonspherical harmonics showed similar SK maneuver planning behaviors to those of the cases with 660 by 660, current work only considered 660 degree and 660 order of nonspherical harmonics for the remaining simulations. Applying the full degree and order of nonspherical harmonics will minimize the uncertainties while establishing the SK maneuver strategy, although it consumes considerable computation time.
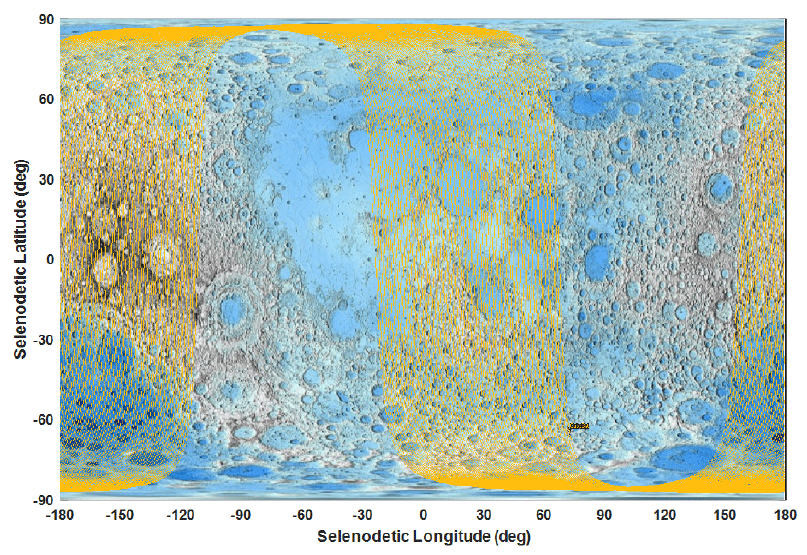
To determine more details on the phenomena previously discussed, a lunar ground track for the time span of 12.5–21 days since the epoch (boxed areas with dotted red line in Fig. 3) was plotted, as depicted in Fig. 4. To achieve this, a cylindrical lunar digital elevation map (DEM) was overlapped with the ground track of a spacecraft. This cylindrical map is based on data from the Lunar Orbiter Laser Altimeter on the NASA LRO spacecraft (Smith et al. 2010), and can be obtained from (USGS 2019). Two colors (blue and steel) are used to express elevation within the map, and the elevation values are the distance above or below the reference sphere. The darker blue color indicates a deeper valley, while higher hills are expressed with darker steel colors (black). Unsurprisingly, the plotted lunar ground track almost matched the far side of the Moon (selenocentric longitude –180° to –90°, 90° to 180° area), where the lunar surface is greatly irregular, namely, there is a large difference in elevation, even with small-size craters, than that on the near side of the Moon. This result confirms the phenomena shown through Fig. 3 and emphasizes the importance of considering a proper degree and order of nonspherical harmonics while analyzing the orbital characteristics, particularly when flying at extremely low altitudes.
Considering 660 degree and 660 order of nonspherical harmonics of the Moon, four different sets of orbitmaintaining cases with different reference altitudes and deadband conditions were simulated and the associated results are shown in Table 3. Regardless of the different reference altitudes considered, it was found that an average execution of SK maneuvers per 0.7–0.8 day is necessary for the ±5 km deadband case, and per 1.8–2.1 days for the ±10 km deadband case during the one-month period. For the total delta-V magnitude, approximately 47.63–63.98 m/s is necessary to maintain the ±5 km deadband, while approximately 34.43–43.30 m/s is necessary for the ±10 km deadband case. Unsurprisingly, a higher reference altitude and a larger deadband width both require a lower total delta-V to maintain the reference altitude, as can be observed in Table 3. However, some exceptions can be seen in Table 3; the 30-km reference altitude with ±10 km deadband requires 34.43 m/s of delta-V, which is ~1.72 m/s less than the case with a 40-km reference altitude and ±10 km deadband. This phenomenon is mainly due to the difference of the last SK maneuver time. As shown in Table 3, the last maneuver execution time for the 30-km reference altitude case is 27 January 2025 23:10:22.755 (UTC), which is approximately two days earlier than the 40-km reference altitude case, shown to be at 29 January 2025 22:18:14.508 (UTC). Considering an average maneuver execution time (approximately 1.8–2.1 days, as discussed) for the ±10 km deadband case, an additional SK maneuver will be necessary to maintain the 30-km reference altitude, and finally will result in a total delta-V near ~36.89 m/s, which is slightly more than the delta-V for the 40-km reference altitude case. Here, it is noted that 36.89 m/s of total delta-V was simply computed by adding 2.46 m/s to 34.43 m/s, where 2.46 m/s is the estimated mean delta-V magnitude per maneuver.

|
Based on the delta-V results obtained together with the performance of a miniaturized propulsion system currently available, this subsection studies the feasibilities of maintaining such an extremely low altitude using a CubeSat. Due to the extensively growing interest in CubeSat applications, several propulsion systems have been rapidly developed with enhanced performance for use with CubeSats. For example, the miniaturized propulsion system for the NEAScout mission has been designed to provide approximately 37 m/s of delta-V for a 14 kg CubeSat. The MarCO mission used 40 m/s of total delta-V for a 13.5 kg CubeSat and approximately 237 m/s of delta-V for a 14 kg CubeSat for the Lunar Flashlight mission (VACCO 2019). Among the 4 different reference altitude cases shown in Table 3, maintaining the reference altitude of 20 km would not be an attractive choice due to CubeSat flight safety itself, as the height of the highest mountain on the Moon is approximately 12 km (Beckman & Lamb 2007).
From the delta-V in Table 3, a ~15 kg class CubeSat can maintain a 30–50 km reference altitude with a ±10 km deadband orbit during a one-month period using the same miniaturized propulsion system as those of the NEAScout and MarCO missions. With the propulsion system of the Lunar Flashlight mission, the total mission duration can be extended up to approximately 6 months. For a ±5 km deadband, maintaining a 30–50 km reference altitude, it seems that approximately three weeks and ~4.4 months of mission operation is possible with the same propulsion system as those of the NEAScout and MarCO missions, and the Lunar Flashlight mission, respectively. However, as current estimates of mission durations are entirely based on ideal delta-Vs, the real-world estimated mission duration would be less than that of the current estimates if further details of operational constraints are regarded while estimating the expected mission duration with a CubeSat. Among the two deadband cases (±5 km and ±10 km), the ±10 km case seems to be preferable regarding following real-world operational aspects, such as: maximizing the payload operation time, payload data dumping time, and bus stabilization time before and after maneuver execution, among others.
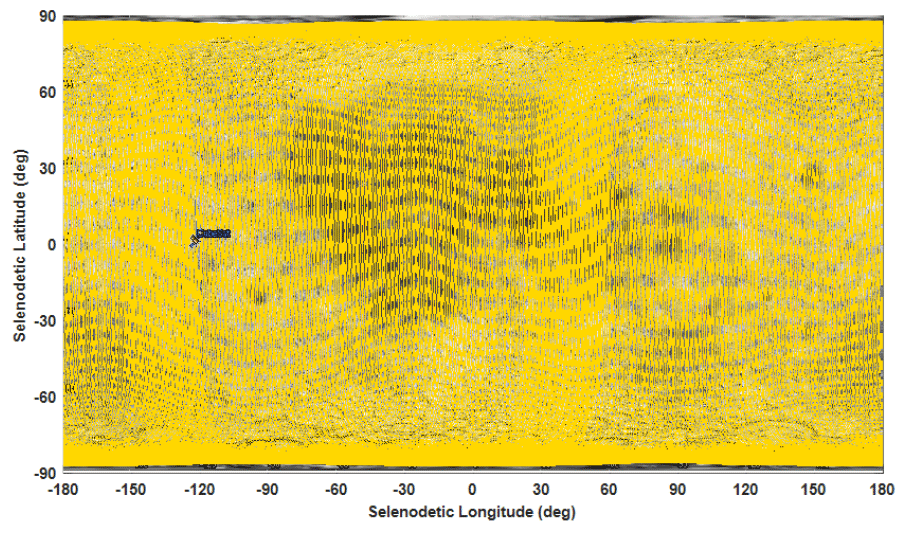
As an example, the orbital characteristics of a CubeSat having a 30-km reference altitude with a ±10 km deadband is analyzed in more detail. Maintaining a reference altitude of 30 km with a ±10 km deadband would have a mean orbital period of approximately 1.85 h, and the lunar ground track for this orbit will shift by approximately 1° (~30 km apart in lunar ground distance) per orbit. Therefore, a oneday lunar ground track shift would be approximately 12.97°, indicating that almost full coverage of the lunar surface is possible within a one-month period. In Fig. 5, the lunar ground track during the one-month period for this orbit is depicted, demonstrating that the lunar surface can be fully covered during one month. If we assume a camera is onboard this CubeSat, approximately 30° of a half-cone angle field of view would be enough to cover 30 km of lunar ground track shift per orbit, with approximately 3–4 km of overlapping ground distance. Moreover, the other two reference altitude cases (40 and 50 km) have almost the same orbital characteristics, as previously explained, as the reference altitude differences are too small to expect large differences in the orbital characteristics between them.
5. CONCLUSIONS
The current work analyzed delta-Vs for maintaining an extremely low altitude on the Moon. Further, the possibilities of applying a CubeSat mission were investigated. The associated SK problem at this low altitude was formulated using the STK Astrogator module by AGI, which has been used to design and operate many real flight missions. The targeting problem for the SK maneuvers was formulated by establishing a MCS with high-fidelity force model. A total of eight different extremely low reference orbit sets for a circular polar orbit around the Moon, having four different reference altitudes above the mean lunar surface (20, 30, 40, and 50 km) and two different deadband sets (±5 and ±10 km) were applied to each of them for the simulation. As a result, characteristics of the SK maneuvers were successfully analyzed together with the effect of the selection of the degree and order of the lunar gravitational harmonics on the overall SK maneuver strategy. As expected, a considerable magnitude of delta-Vs, as well as the SK maneuver execution time were affected by these different selections. The main cause of the observed phenomena was again confirmed, as originated from the orbit propagation uncertainty accumulation while flying around the far side of the Moon. Regardless of the different reference altitudes considered, it was found that an average of the execution of SK maneuver per 0.7–0.8 day is necessary for the ±5 km deadband case, and per 1.8–2.1 days for the ±10 km deadband case during the one-month period. For the total delta-V magnitude, approximately 47.63–63.93 m/s is necessary to maintain the ±5 km deadband, and approximately 34.43–43.30 m/s for the ±10 km deadband case. Based on the derived overall SK maneuver delta-Vs cost, the possibilities of performing a CubeSat mission were additionally analyzed with application of the current flightproven miniaturized propulsion system performances. It is concluded that a ~15 kg class CubeSat could maintain an orbit (30–50 km reference altitude having ±10 km deadband limits) around the Moon from 1–6 months. In addition, maintaining the CubeSat at a given reference orbit during the one-month period showed almost full coverage of the lunar surface, which may play a very important role in the scientific data return point of views. However, the estimated mission lifetime of real-world operation would be less than the current estimate, as the current estimate is entirely based on ideal SK maneuver delta-Vs. The current work may represent a good starting point for more detailed trajectory designs and analyses to realize a CubeSat mission for an extremely low altitude on the Moon.










