1 INTRODUCTION
Temperature and wind observations are essential to understanding the dynamics and energy budget of the atmosphere. The mesosphere and lower thermosphere (MLT) are highly variable because of various wave activities in the lower atmosphere and several effects from space (Fritts & Alexander 2003). The determination of the exact temperature and wind in the MLT region is therefore of great importance. In the past, studies of the MLT region were significantly limited due to the inaccessibility of this region. With the development of various instruments (e.g., Meteor Radars; MRs, Fabry- Perot interferometers; FPIs, and medium-frequency radars), research about the MLT region has become more active compared with that a decade ago. A MR can measure neutral winds at altitudes ranging from 80 to 100 km throughout the year for 24 hr, regardless of the weather. Thus, the daily mean temperature near the mesopause can be estimated (Lee et al. 2016). An FPI is a very sensitive optical instrument that can measure airglow emissions at specific wavelengths (i.e., OH 892.0 nm, OI 557.7 nm, OI 630.0 nm) to simultaneously obtain both wind and temperature data at altitudes of airglow layers in the MLT region (e.g., Lee et al. 2017).
The King Sejong Station (KSS) in Antarctica (62.22°S, 58.78°W) has been operating an MR to study the neutral dynamics in the MLT region since 2007 (Jee et al. 2014). In addition, an FPI was installed at the KSS in 2017, making it possible to more actively conduct research on the MLT. Both instruments have the advantage of measuring neutral winds and temperatures in the MLT region, but the MR and FPI winds are obtained with fundamentally different methods. In case of the MR, the neutral wind data are derived from drifting information on meteor echoes observed in each altitude bin assuming that the meteor plasma trail moves together with the neutral atmosphere (Holdsworth et al. 2004). In case of the FPI, however, the underlying assumptions are that the height distribution of the airglow intensity remains constant and the winds are divergence-free within the field of view of the FPI during the observation.
In this study, we compare neutral wind data obtained with the FPI in the OH 892.0 nm and OI 557.7 nm airglow layers with winds simultaneously observed with the MR to confirm the reliability of the newly installed FPI. The instruments and measured wind data are described in Section 2. The results and a discussion are presented in Section 3. A conclusion is provided in Section 4.
2 INSTRUMENTS AND DATA
The MR at the KSS has been used to observe the MLT region since its installation in March 2007. Unlike other optical instru-ments, this instrument has the advantage of being able to continuously detect echoes from meteor trails for 24 hr, regardless of the daylight or weather conditions.
As a meteor enters the atmosphere, its kinetic energy is converted into thermal energy by the collision with atmospheric molecules and a cylindrical plasma trail forms in the path of the meteor. When the radio waves transmitted from the MR are perpendicular to the meteor trail, the radio signal scattered by electrons in the meteor trail is returned to the receiving antennae. Finally, the built-in analysis software is used to analyze the received signals and provides the altitude, distance, meteor speed, and radial velocity of the meteor echoes (Murad & Williams 2002). The background wind speed can be obtained from the radial velocity of the meteor echoes within 1 km and 1 hr bin using the least squares method (Holdsworth et al. 2004).
After upgrading the transmission power to 12 kW in 2012, the KSS MR has been able to detect 15,000–40,000 meteors per day with a notable seasonal dependence. The KSS MR operates at 33.2 MHz with a maximum duty cycle of 8.4 %. The analysis process is similar to that of the MR at Buckland Park (Holdsworth et al. 2004). Detailed operating parameters of the KSS MR are summarized in Table 1.
The FPI was installed at the KSS in February 2017. The FPI includes two modules: an electronic module that controls an optical instrument and an optical module for the observation of airglow emissions. The structure of the FPI is shown in Fig. 1. The optical module is composed of a sky scanner, a filter wheel, an etalon chamber, focal lenses, and a CCD camera under the dome. All optical components, except for the sky scanner, are fixed to the optical frame, which is covered with a dark sheet as shield from stray light. As an initialization process of the observation, the sky scanner moves to the laser position. After the laser interference image of a calibration laser emission line (632.8 nm) is recorded in the CCD camera, regular airglow measurements are performed using three filters (OH 892.0 nm, OI 557.7 nm, OI 630.0 nm) for different airglow emissions. The OI 630.0 nm measurement is carried out with an exposure time of 5 min; the other measurements were performed with an exposure time of 3 min. Each measurement consists of an observation of the vertical (zenith) and cardinal points (north, south, east, and west). One observation cycle has a duration of approximately 50 min. The observed data are analyzed with software developed by the High Altitude Observatory, National Center for Atmospheric Research, USA (Wu et al. 2012).
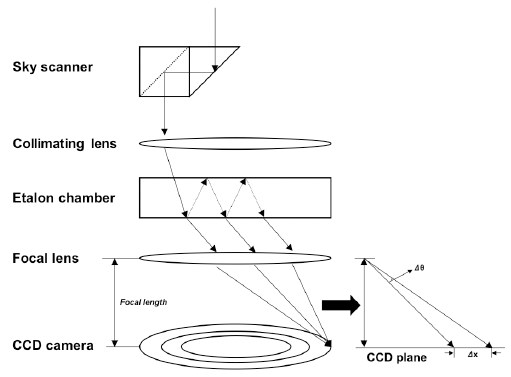
The principle of the FPI observation is as follows. First, the airglow enters the etalon chamber through the sky scanner. The monochromatic airglow light is captured in an interference image based on the repetition of transmission and reflection inside the etalon chamber. If the source of the airglow moves, that is, approaches or moves away from the observer, the incidence angle of the light forming the interference images becomes large or small, respectively. When the incidence angle of the light changes by Δθ, the image on the CCD is displaced by Δx = fΔθ (f: focal length). Thus, the drift velocity can be calculated using the Doppler shift (Wu et al. 2002, 2012).
Because the FPI observes the airglow light from the MLT region, it is critically affected by the weather conditions. Therefore, the wind and temperature data from the FPI for cloudy days are unreliable. A thorough data selection criterion must be established to control the data quality. The FPI is equipped with a cloud detector that uses infrared light to determine the amount of clouds. Details about the cloud index are presented in Table 2. Because the FPI also provides wind errors for the wind measurements, we used the data with wind errors below 20 m/s in this study (Section 3.1) to obtain large enough FPI wind data for the long-term comparison with the MR wind measurements. Beyond Section 3.1, we selected wind data with errors below 10 m/s and a cloud index 1 representing clear sky. As a result, only 16 % of the FPI wind data were used for the comparison.
3 RESULTS AND DISCUSSION
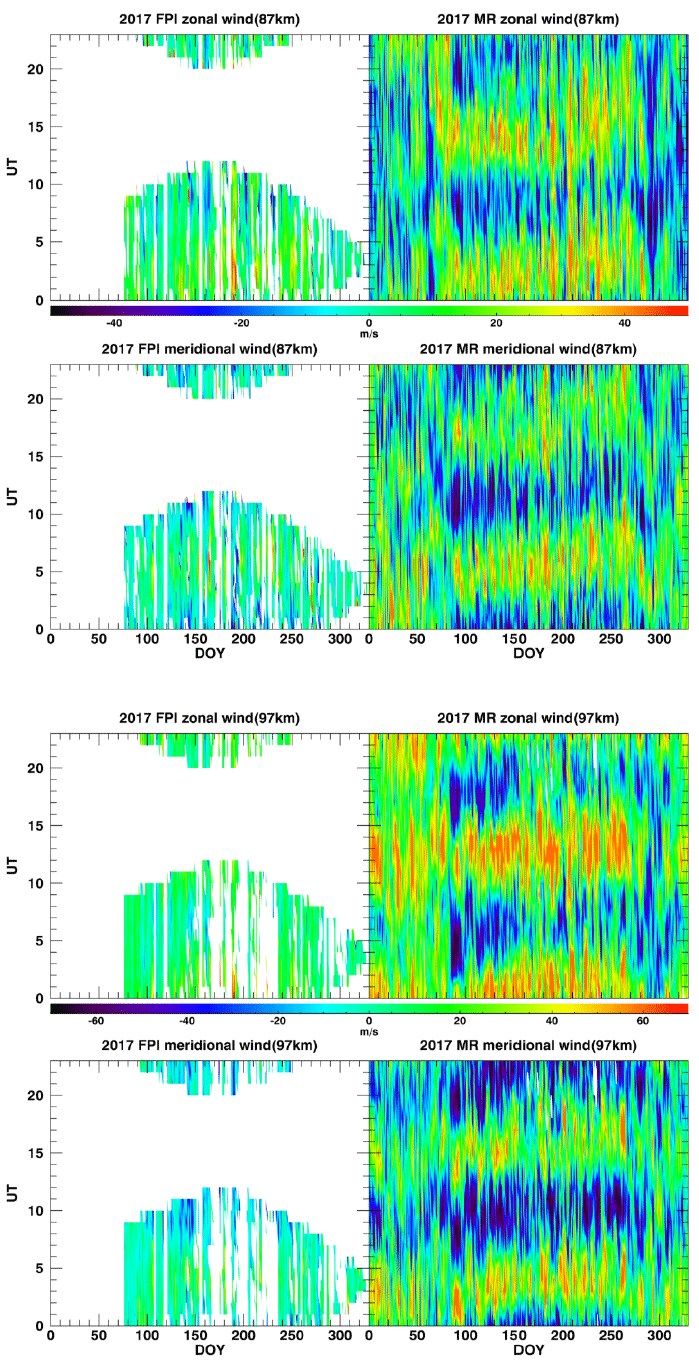
Fig. 2 shows the hourly wind data at altitudes of 87 and 97 km measured by the FPI (with filters for OH 892.0 nm and OI 557.7 nm airglows) and MR as function of the day of year (DOY) and universal time (UT). The weather conditions defined by the cloud index significantly affect the wind error during FPI data analysis, resulting in a limited time coverage of the wind observations. Although the individual wind values from FPI and MR significantly differ from each other, their local time variations are in good agreement over the entire observation period in 2017. For example, both the FPI and MR simultaneously observed strong eastward zonal wind flow at 87 km (97 km) at ~02:00 UT (01:00 UT) and strong westward wind at ~07:00 UT. With respect to meridional wind, the two instruments measured consistent wind features; southward wind at ~01:00 UT (24:00 UT) at 87 km (97 km) and northward wind at ~05:00 UT (08:00 UT) at 87 km (97 km).
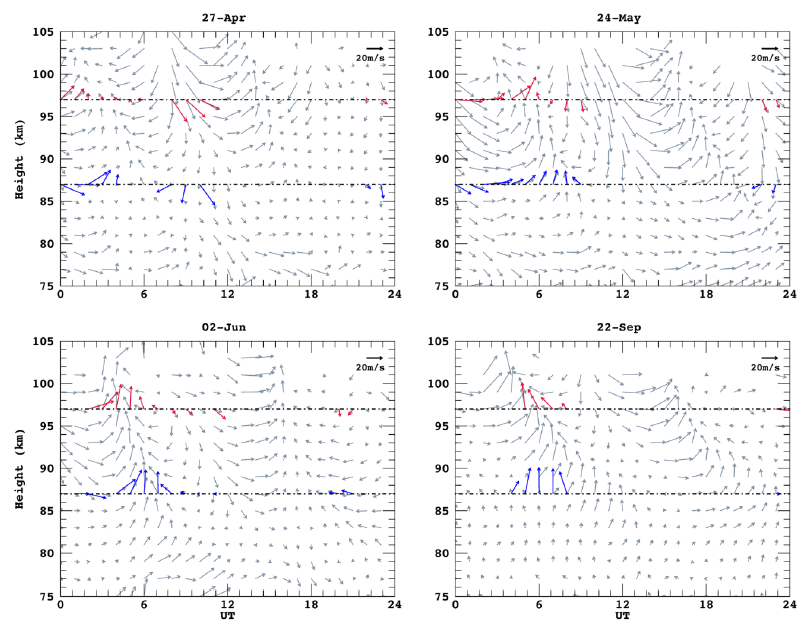
To compare the winds from the FPI with those from the MR on an hourly basis, we selected four independent days with continuous FPI wind measurements under good weather conditions. Fig. 3 shows the hourly wind vectors from the FPI at 87 and 97 km as a function of the UT and height. The wind vector fields from the MR for altitudes from 75 to 105 km are also presented. Although the FPI winds match the MR winds at 97 km, significant discrepancies are observed at 87 km.
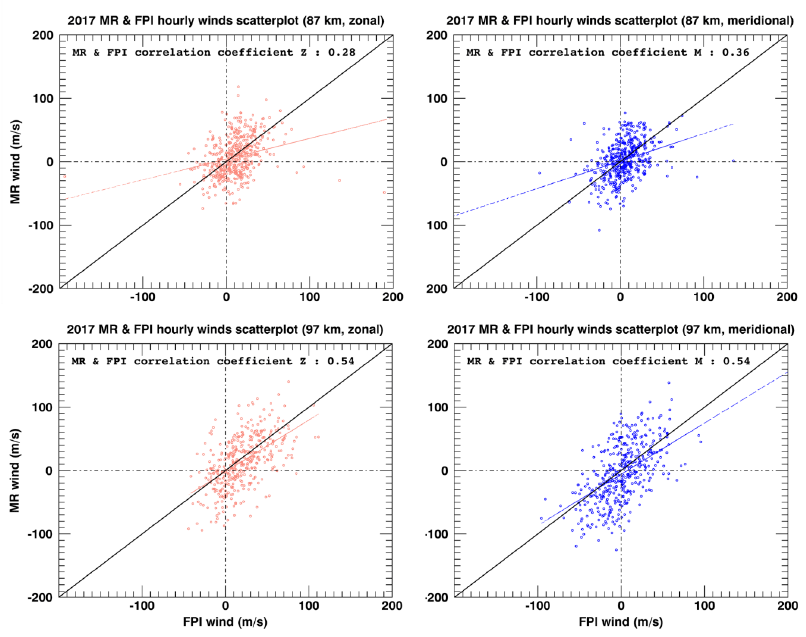
For a quantitative comparison, we calculated the correlation coefficients between the FPI and MR winds. Fig. 4 displays the scatterplot of the hourly FPI winds and MR winds for the period from March to November 2017. The black and colored lines indicate the 1:1 line and regression line, respectively. The correlation coefficients are 0.28 for the zonal wind and 0.36 for the meridional wind at 87 km. The correlation coefficients are 0.54 for the zonal wind and 0.54 for the meridional wind at 97 km. They are significantly larger than those at 87 km, which will be discussed in Section 3.2. Another notable feature is that the FPI winds are consistently stronger than the MR winds in the two height layers, which may be due to the shorter time integration of the FPI than that of the MR. The FPI only needs 6 min to obtain a wind in a single direction, while the MR calculates one-hour average winds.
Because the FPI collects the emission from an airglow layer with a finite height, the FPI winds can be regarded as weighted mean values with the height distribution of the airglow intensities centered at 87 or 97 km, respectively. The full width at half maximum (FWHM) of the OH and OI airglow layers is ~10 km (Baker & Stair 1988; Yu et al. 2016). To consider the airglow height distribution in the comparison between the MR and FPI winds, we computed the weighted mean values of MR winds by assuming a Gaussian distribution with a FWHM of 10 km and peak height of 87 km and 97 km for the OH and OI layers, respectively.
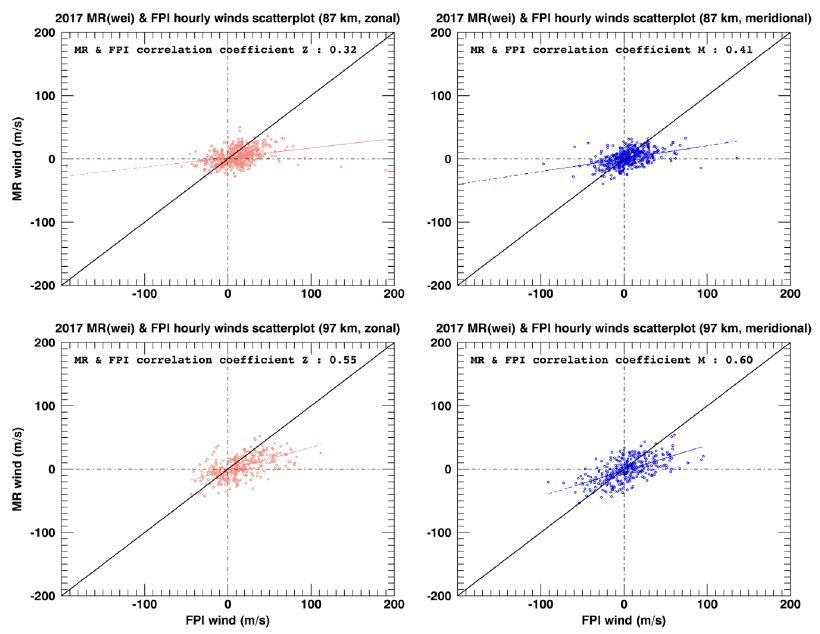
Fig. 5 is similar to Fig. 4, but the FPI winds are compared with the weighted mean MR winds according to the airglow emission profile specified above. Overall, the correlation coefficients increase compared with those shown in Fig. 4. The correlation coefficients are 0.32 (0.55) for the zonal wind and 0.41 (0.60) for the meridional wind at 87 km (97 km). However, the absolute values of the weighted mean MR winds significantly decrease; therefore, the slopes of the fitting lines deviate from the 1:1 line.
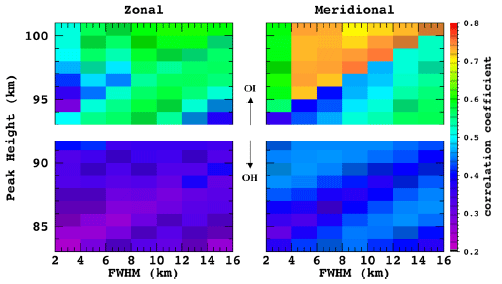
To determine an optimal FWHM and central height for the airglow layer, we arbitrary varied the FWHM from 2 to 16 km with a step size of 2 km and the peak height of the OH (OI) layer from 83 km (93 km) to 91 km (101 km) with a step size of 1 km. Fig. 6 displays the correlation coefficients between the FPI and weighted mean MR winds for the aforementioned conditions. The correlation coefficient obtained by changing the FWHM at a fixed peak height of 87 km or 97 km shows no significant change. At a fixed FWHM of 10 km, the correlation coefficient considerably changes with the peak height; the highest correlation coefficient is obtained at a peak height of 88–89 km (97–98 km) for the OH (OI) airglow layer. This is consistent with peak height estimations for airglow layers based on previous studies (Marsh et al. 2006; Yuan et al. 2013; Yu et al. 2017). We also note that the correlation coefficient of the OI layer is significantly higher than that of the OH layer. This result is opposite to that of Yu et al. (2016) who reported a much higher correlation coefficient for the OH layer compared with that for the OI layer. This discrepancy may be related to the unique location of the KSS. It is well known that the gravity wave activity is rather strong in the Antarctic Peninsula region (e.g., Wu & Jiang 2002; Lee et al. 2013). In fact, Kam et al. (2017) reported that the number of wave events at 87 km is significantly larger than that at 97 km over the KSS. In addition, Wu et al. (2013) showed that the gravity wave activity affects the airglow emissions below 88 km at Rothera (67°S, 68°W), a station neighboring the KSS. The spatial distribution of the airglow emissions may thus vary because of gravity waves (Manson et al. 1996).
4 SUMMARY AND CONCLUSION
The FPI was installed at the KSS, Antarctica, in 2017. To verify the reliability of the FPI data, we compared the FPI winds with MR winds that were simultaneously measured at the same location. The comparison of the first-year FPI wind dataset shows that the overall characteristics of the FPI winds are consistent with that of the MR winds at 97 km. The correlation coefficients between the two winds are 0.28 and 0.54 for the zonal component and 0.36 and 0.54 for the meridional component at 87 and 97 km, respectively. Because the FPI winds are weighted averages obtained along the height profile of the airglow emissions, we computed the weighted mean values of the MR winds by assuming a Gaussian function with a FWHM of 10 km and OH and OI airglow layer peak height of 87 km and 97 km, respectively. The correlation coefficients between the FPI and weighted MR winds improve, as expected, but the magnitudes of the weighted MR winds significantly decrease due to the averaging. We further investigated how the correlation changes depending on the assumed FWHM and peak height. The best correlation for the OH and OI airglow layers was obtained at a peak height of 86 km and 97–98 km, respectively. The best peak heights are consistent with that reported in other airglow studies. However, the overall correlation coefficients of the FPI winds with the MR winds are significantly lower than that of other studies based on FPI wind observations. This may be related to the strong wave activity over the Antarctic Peninsula. A further study will address the effect of the waves on the winds measured with the FPI.











