1 INTRODUCTION
Halo coronal mass ejections (CMEs) caused by solar activities affect the geomagnetic field and result in geomagnetic storms (Cho et al. 2004). Solar activity research is currently underway in Korea (Hwangbo et al. 2015; Lee 2015). Geomagnetic storms have an impact on communications, global positioning system (GPS), satellites, geological exploration, electrical power grids, geomagnetically induced currents (GICs), and steel cables. As society continues to rely on these systems, more effort is being exerted to prevent damage from geomagnetic storms (Ahn 2000; Choi et al. 2005; Choi et al. 2015; Chung et al. 2015; Mengist et al. 2016). To reduce damage caused by geomagnetic storms resulted from halo CMEs impacting Earth, domestic and international space weather institutes provide CME lists. Since 1996, NASA has provided a CME list obtained through the processing of large angle and spectrometric coronagraph (LASCO) images of the solar and heliospheric observatory (SOHO) satellite (https://cdaw.gsfc.nasa.gov/CME_list/halo/halo.html). This list provides information including the detection time of the LASCO C2 camera, the apparent speed, space speed, acceleration, measurement position angle (MPA), source location, X-ray importance, and flare onset, in addition to all other CME lists including partial CMEs (https://cdaw.gsfc. nasa.gov/CME_list/). European Space Agency (ESA) provides a list obtained through computer aided CME tracking (CACTUS) software using LASCO images (https://sohowww. nascom.nasa.gov//data/REPROCESSING/Completed/). CACTUS is automated software used to detect CMEs (http:// sidc.oma.be/cactus/).
Meanwhile, the Korean Space Weather Center of the National Radio Research Agency developed a CME analysis model program in 2013, which provides information services on the occurrence of CMEs. The CME analysis model detects CMEs through an image processing technique utilizing three sources of image data: solar terrestrial relations observatory (STEREO) A, B, and LASCO C3. For each CME detected, the acquired geometrical information is integrated and matched to the CME. For a successful match, geometrical physical 3-D quantities are eventually produced and the arrival time of the CME at Earth is provided. However, in many cases, the STEREO A, B data are unavailable for this model, and thus, there have been difficulties in its proper operation. In 2015, an improvement was made to produce 2-D results using LASCO images only when the STEREO data are unavailable.
In this study, the cone model was applied to detect halo CMEs and produce 3-D parameters utilizing SOHO LASCO C3 images only. The cone model estimates the geometrical and dynamical characteristics of halo CMEs based on the following three assumptions: (1) CMEs move in a radial direction with a fixed angular interval through the corona, (2) the origin of a halo CME is an active region of the solar surface adjacent to the center of the solar disc, and (3) the bulk velocity direction of a CME is radial, and a CME expansion is isotropic (Zhao et al. 2002). Prior to a study by Zhao, it was shown that the cone model provides a reasonable estimate (Fisher & Munro 1984; St. Cyr et al. 2000; Webb et al. 2000). In addition, Xie et al. (2004) extended the cone model by Zhao et al. (2002), verified its validity, and used it to predict the CME propagation time based on a real radial velocity. Taktakishvili et al. (2009) studied the performance of a combination of the halo CME cone analysis model and ENLIL 3D magnetohydrodynamics (MHD) heliosphere model. The ENLIL model is a simulation model that predicts solar wind progress by inputting solar wind information near a solar radius of 21.5 (Odstrčil et al. 2003). Pulkkinen et al. (2010) generated 3-D characteristics based on a conic CME approximation, and proposed a new method for determining the cone model parameters from halo CMEs. With this method, the CME mass is estimated from white light coronagraph images, and a new type of parameter distribution is used to produce cone model parameters through a standard image processing technique. Jackson et al. (2013) showed that a CME forecast is possible through IPS observations using radio arrays from the Institute for Space-Earth Environment Research (ISEE). Mays et al. (2015) evaluated the CME arrival time at Earth using the Wang-Sheeley-Arge (WSA)-ENLIL + cone model installed at a Community Coordinated Modeling Center (CCMC). Yun et al. (2016) determined the best parameter combinations for achieving the highest performance of the ENLIL model.
In this study, we developed an automated halo CME analysis model based on the original cone model (Zhao et al. 2002) and the cone model modified by Xie at al. (2004) for 3-D parameter generation, and by applying the parameter derivation formula by Pulkkinen et al. (2010). Section 2 describes the proposed halo CME detection algorithm. In Section 3, the image processing technique is described to derive the morphological and dynamical characteristics. In Section 4, test results of the automated halo CME analysis model are shown, and in Section 5, some concluding remarks are provided.
2 AUTO-DETECTION PROCESS FOR HALO CME
LASCO C3 images are coronagraphs observed for an extensive range of 3.7–32.0 solar radii from the solar center. Thus, these images are adequate to detect halo CMEs that originate from the sun and propagate to Earth. Fig. 1 shows a LASCO C3 image taken at 01:54 UT on Feb. 25, 2014. In the lower-left portion of the figure, we can see that a halo CME eruption occurred.

We developed an algorithm for detecting halo CME eruptions using LASCO C3 images of SOHO. The overall detection process is as follows:
3 ALGORITHM FOR MORPHOLOGICAL AND MECHANICAL PROPERTIES OF HALO CME
The image processing technique for each step of the halo CME eruption detection algorithm is described as follows:
-
- Transform original LASCO C3 images into monochrome images through preprocessing
-
- Extract the region of interest from the RDIFF images obtained from the preprocessed images
-
- Test and apply various filtering technologies to remove noise from the RDIFF images excluding CME shapes
-
- Extract CME shapes from the denoised RDIFF images and apply morphological image processing technique to remove extra noise
-
- Apply the cone model to obtain basic information of identified halo CME
To detect the eruption of a halo CME, an original LASCO C3 image at the time of interest (t) and an image of previous time step (t−1) are converted into a monochrome image.Fig. 2

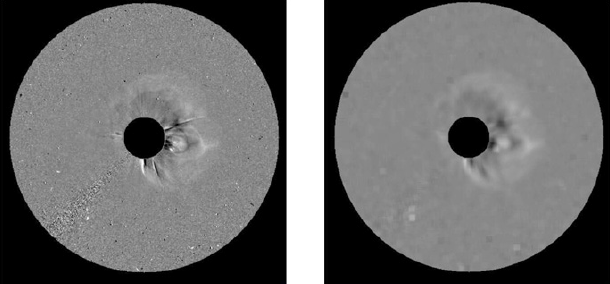
In addition to halo CMEs, LASCO C3 images have background noise, and halo CMEs can be identified easily without such noise. To remove the noise, two monochrome images are utilized to generate an RDIFF image. The RDIFF image is used to remove the background field easily. Unlike with CMEs, the background field does not change significantly over time. An example of a background field is the continual release of solar wind from the sun. As shown in Fig. 3, a LASCO C3 image taken at 17:18 on Apr. 4, 2000 and an image of the previous time step at 16:43 were converted into monochrome images, and an RDIFF image of 17:18 was obtained from the difference between the two images. In this RDIFF image, the CME can be identified more easily compared to the monochrome images because the background field was removed to highlight the CME shapes. In addition, we can identify superfluous regions around the solar perimeter and the image boundary from this RDIFF image. This can also be identified in the original image or in a monochrome image. Once the superfluous regions are identified, only the regions of interest are extracted for subsequent processing. To remove the unnecessary regions, the center of the image is identified, and the regions of interest are extracted in reference to this center to conduct the subsequent process. As shown in Fig. 4, unnecessary regions are processed to appear in black, and in the subsequent process, the image processing is applied only for non-black regions.


To remove only noise from RDIFF images, while leaving the CME shapes untouched, various filtering techniques were applied and tested. This process is called the primary noise removal. The filtering techniques tested are the median technique, smoothing technique, and Lee filter technique, as described below.
-
- Median technique: Because the median value is produced for each range, no skewness is observed even when the extremum is included
-
- Smoothing technique: Because the arithmetic mean is generated for a fixed interval of range, the skewness is observed when the extremum is included.
-
- Lee filter technique: This is an adaptive filtering technique that depends on the local characteristics of the surrounding pixels.
With the median and smoothing techniques, the amount of removable noise can be adjusted by modifying the kernel size on the image, whereas with the Lee filter technique, the amount of noise can be adjusted by changing the size of the filter box. The amount of noise removed is proportional to the sizes of the kernel and filter box. When adjusting the size of the kernel or filter box, the optimal size required to remove noise only from the image, while leaving the CME shape untouched, is determined through trial and error. In this study, a kernel size ranging from 5 to 15 was tested for the median or smoothing technique, whereas the filter box size ranging from 5 to 15 was tested for the Lee filter technique. The test results indicate that the optimal size of both the kernel and filter box to remove only noise without affecting the CME shape is 11. These three techniques were applied for RDIFF images, as shown in Figs. 5, 6, and 7. As a result, it was found that the noise was removed in the CME shape of an RDIFF image. However, the degree of noise removal differs depending on the technique applied. In particular, it is possible to visually identify noise in the lower left area of the image for both the smoothing and Lee filter techniques. Thus, according to the application results of the three filtering techniques to the RDIFF images considered in this study, it was found that the median technique is most effective at removing noise when compared to the smoothing and Lee filter techniques.


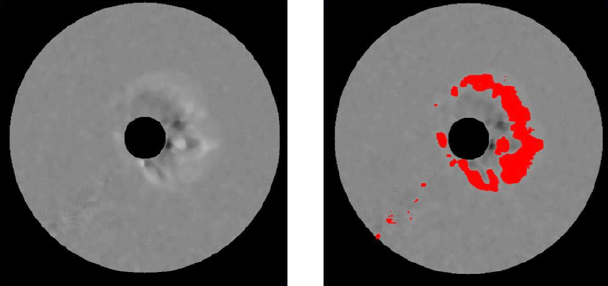
To discern CME shapes visually from RDIFF images with the primary noise removed, we analyzed the pixels of the CME shapes in the images. The threshold value, which is the minimum pixel value of a CME shape, is determined based on an analysis of 17 halo CME events erupted during the period of 2000 to 2015. Information on these 17 halo CMEs is summarized in Table 1. According to the analysis results of previous halo CME events, it was found that the pixel values of the CME shapes in the RDIFF images are greater than 4. Hence, the threshold value of the CME shapes is determined to be 4 in the RDIFF images. To distinguish CME shapes in the RDIFF images with the primary noise removed, a masking image processing technique was applied, and pixels with values of greater than 4 were considered as belonging to CME shapes.
-
- Masking technique: This is a technique used to filter pixels satisfying the specific conditions in an image. Fig. 8 shows an RDIFF image without filtering the primary noise, and the resulting image with pixel values of greater than 4 shown in red. As a result, the CME shape and noise in the image appear at the same time. Fig. 9 shows an RDIFF image with noise removed using the median technique, and an image with pixel values of greater than 4 shown in red. However, we can see that this case also shows some noise in addition to the CME shape. To remove this extra noise, an enhanced image processing technique, that is, a morphology open technique, was applied to this image. We call this process secondary noise removal.
-
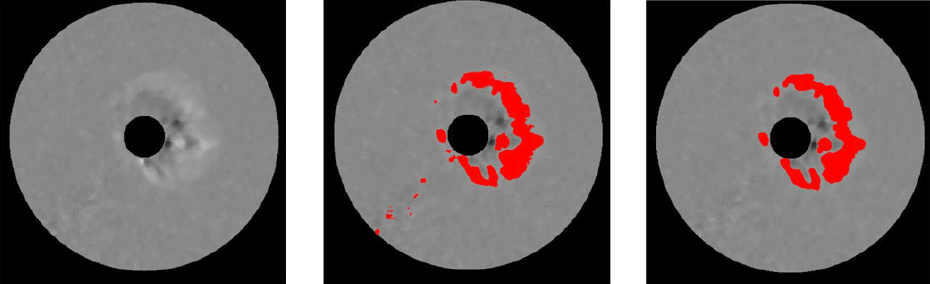
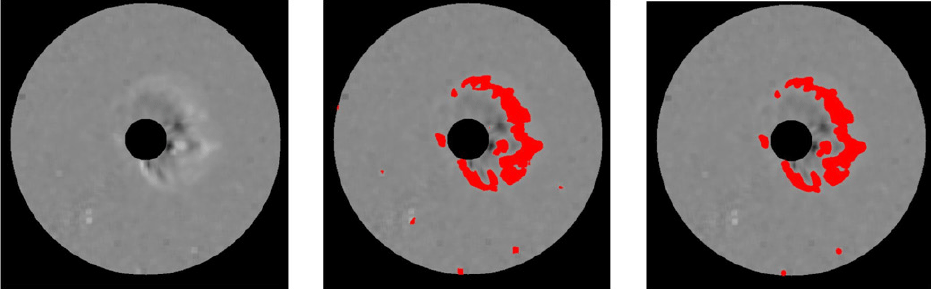
- Morphology open technique: This is a technique to simplify large and significant shapes in an image, remove small shapes, and highlight the shapes of interest. Fig. 10 shows an RDIFF image with the primary noise removed (left-side image) using the median technique, and an image with the CME shape extracted with some noise appearing in the lower left (middle image). After applying the morphology open technique to the image to remove secondary noise, the resultant image shows a CME shape without noise (right-side image). An RDIFF image with the primary noise removed using the smoothing technique is shown on the left side of Fig. 11, and an image of the extracted CME shape is shown in the middle of Fig. 11, with some noise appearing in the lower left of the image. After applying the morphology open technique to this image to remove secondary noise, a little noise remains at the bottom of the image (rightside image). Fig. 12 shows an RDIFF image with the primary noise removed using the Lee filter technique (leftside image) and an image of an extracted CME (middle image). This figure shows more noise compared to that of the median or smoothing technique. When we apply the morphology open technique to this image we can see that noise can be completely removed, but with a sacrifice in some of the CME shape (right-side image). Extracting CME shapes by first applying the median technique to remove the primary noise, and then removing the secondary noise, was demonstrated to be the best approach for the timeline of 17:18 UT on Apr. 4, 2000.


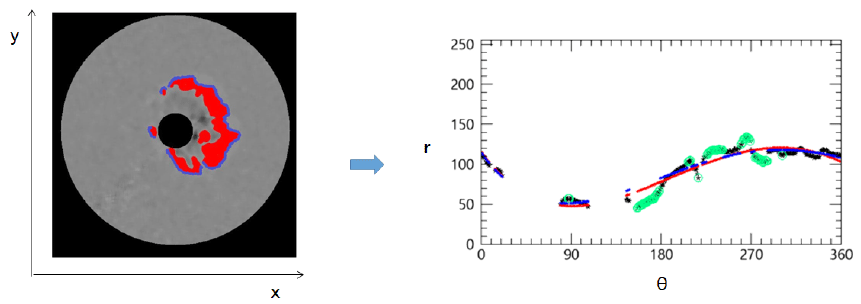
According to LASCO C3 images, halo CMEs heading toward Earth propagate radially from the center of the sun. In other words, the erupted halo CMEs are emitted almost circling the sun. Based on this feature, to distinguish a halo CME, the radial boundary of the CME shapes extracted from the image, that is, the interface, is determined. When the angular distribution of the interface for a CME shape is greater than Δ90˚, it is defined as a halo CME. The interface is determined after converting the Cartesian coordinate system [x, y] of the CME shapes extracted from the LASCO C3 images into a polar coordinate system [r, θ]. Fig. 13 shows a CME shape (red) extracted from an RDIFF image with median filtering applied (left-side image), with the radial boundary from the solar center, that is, the CME interface, shown in blue. The CME shape extracted from the RDIFF image in Cartesian coordinates is converted into polar coordinates, and the interface of the CME is defined as the pixel with the largest r value for each θ. The black dots in the right-side image of Fig. 13 indicate the interface. In this case, the interface is formed over angles of 75–360° and 0–20°, and the angular distribution is Δ305°, which is greater than Δ90°, and thus this CME is identified as a halo CME.
When a CME is determined to be a halo CME, morphological parameters are produced by applying the cone model to the CME interface. The cone model assumes that the halo CME is a cone shape in order to determine its angular width and propagation orientation, as proposed by Xie et al. (2004). In this model, three coordinate systems are introduced.
-
- Heliocentric coordinate system: xh, yh, zh
-
- Apex-centered right cone coordinate system: xc, yc, zc
The direction of the cone indicates the direction of propagation.
An intermediate coordinate system used to convert the heliocentric coordinate system into an apex-centered right cone coordinate system.
The morphological characteristics of the cone are represented by the longitude α (or ϕ), latitude θt (or λ), and angular width 2ω. Here, (ϕ, λ) indicates the longitude and latitude at the ecliptic plane, and (α, θ) indicates the longitude and latitude at the POS to conveniently determine the cone parameters; in addition, α is the angle between the xh-axis and the cone axis projected on the POS, and θ is the angle between the cone axis and the POS. In other words, the position of the halo CME, and α, θ, ϕ, λ, and ω, indicating a 1/2 angular width, are defined as the morphological parameters, as shown in Fig. 14.
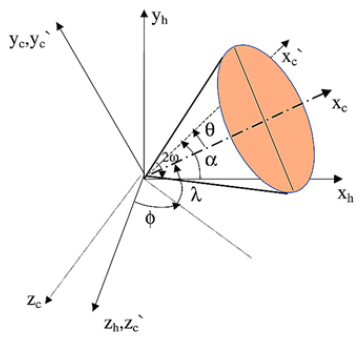
When the circular cross section in the apex-centered right cone coordinate system is projected onto the heliocentric coordinate system, it takes an oval shape, as shown in Fig. 15. That is, a halo CME obtained from LASCO C3 images of the heliocentric coordinate system is assumed as an oval, and using the position of the semi-major and semi-minor axes (a1, a2, b1, b2) of the cone projected from the heliocentric coordinate system, the morphological parameters (α, θ, ϕ, λ, and ω) are produced as follows (Xie et al. 2004):
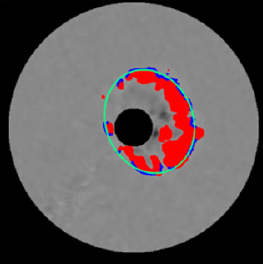
In Fig. 16, based on the CME (red) extracted from an RDIFF image with the median technique applied, the CME interface (blue) was determined, and using this interface, an ellipse (green) was constructed. Using the positions of the semi-major and semi-minor axes of this ellipse, the morphological parameters are determined as α=21.74°, θ=55.51°, ϕ=32.55°, λ=12.11°, and ω=60.59°. When a CME extracted from an RDIFF image using the median technique turns out to be a halo CME, an ellipse (green) is formed, as shown in Fig. 16; otherwise, an ellipse does not appear.
To determine if consecutively detected halo CMEs are from the same event, a matching analysis is required. For this type of analysis, the range of variation of morphological parameters (α, θ, ϕ, λ, and ω) for consecutively detected halo CMEs should be analyzed as a function of time for the same event. Thus, for 17 halo CME event periods observed during the period of 2000 to 2015, the variation in morphological parameters was analyzed, and the range of variation was determined. According to this analysis, when the variation in the position information, θ, ϕ, and λ, is limited to 20°, and the variation in 1/2 angular width, ω, is less than 40° over time, the halo CMEs should be considered to be from the same event. In addition, the lengths of semi-major and semi-minor axes should be increased over time.
When halo CMEs are found to be from the same event, 3-D characteristic factors are determined by utilizing the morphological parameters. These factors are used as an input into the ENLIL-cone model to predict the arrival time of a halo CME at Earth. The resultant 3-D parameters derived to feed into the ENLIL model are as follows:
The actual velocity of a halo CME, Vr, is generated according to the following process based on Xie et al. (2004).
Assuming that a halo CME propagates at an actual constant speed of Vr from the sun, the predicted time when the halo CME arrives at 21.5 Rs, T21.5Rs, is finally calculated as follows:
To develop an automated system for the on-line detection and analysis of a halo CME, a prototype of a CME analysis tool (CAT), which is a 3-D parameter generation program used to produce the characteristic factors, such as the eruption width (ω), eruption location (λ, ϕ), eruption velocity (Vr), and eruption time (), was developed using the interactive data language (IDL) program. The program execution is performed using MAIN_HCME, which is the main procedure, the detailed program description of which is as follows:
-
- Development of a prototype program for the generation of an RDIFF image
READ_LASCO_C3: Converts LASCO C3 images at times (t) and (t-1) into monochrome images
CAL_RDIFF_IMAGE: Produces an RDIFF image utilizing two monochrome images
-
- Development of a prototype program for the removal of the RDIFF image
REMOVE_RDIFF_NOISE: Produces noise-free RDIFF images when applying the median, smoothing, and Lee filter techniques to the RDIFF images
-
- Development of a prototype program for the identification of a halo CME from the RDIFF images
EXTRACT_CME_SHAPE: Extracts CME shapes from the denoised RDIFF images
DETECT_HCME: Identifies a halo CME among the CME shapes and produces morphological characteristic factors
-
- Development of a prototype program for the generation of 3-D characteristic factors
MATCH_HCME: Determines if consecutively detected halo CMEs are from the same event based on morphological characteristic factors
GET_HCME_3D_PARAM: Produces 3-D characteristic factors when consecutive halo CMEs are found to be from the same event
4 VERIFICATION OF CME PARAMETERS AS THE INPUTS OF SOLAR WIND PROPAGATION MODEL
To validate the accuracy of the prototype CAT, the program was tested using the previously selected halo CMEs, and compared with the results of a previous CME analysis model program developed in 2013 (2013 CME analysis model program).
The validation was conducted for 13 halo CMEs observed during the past 4 years, the details of which are summarized in Table 2.
For the 13 events, using the 2013 CME analysis model program and the prototype program developed in this study, the performance of the halo CME event detection was verified, the results of which are summarized in Table 3. For each event, ‘○’ indicates the successful detection of a CME or halo CME, and ‘×’ indicates a failed detection. For ten out of the 13 events, the 2013 CME analysis model program either failed to detect a CME, or the STEREO image (https://stereo-ssc. nascom.nasa.gov/beacon/beacon_secchi.shtml/) availability was inadequate, and thus the 3-D physical quantities were not produced. Thus CMEs were detected and 3-D physical quantities were produced for only the other three events, namely, events 4, 6, and 7. However, the prototype program developed in the present study successfully detected CMEs for 12 events, and failed to detect a CME for only one event, when the median technique was applied. To compare the results with those of the 2013 CME analysis program, tests were conducted on events 4, 6, and 7.
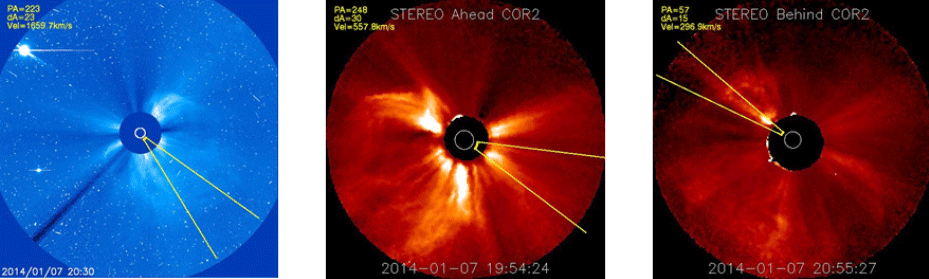
For the halo CME event at 18:23 UT on Jan. 7, 2014, the resultant images obtained from the 2013 CME analysis program are shown in Fig. 19. In Fig. 17, the CME detection results of a LASCO C3 image, SETREO A image, and STEREO B image are shown from the left. The program detected the CME, but failed to detect the halo CME; in the LASCO C3 image of Fig. 17 (left), in particular, the region in yellow, which represents the CME angular width, is narrower than the angular width of the halo CME, which can be identified visually. As a consequence, among the 3-D physical quantities generated, the angular width was determined to be incorrect. The generated 3-D physical quantities are summarized in Table 4.
| T21.5Rs | Vr [km/s] | ω[°] | ϕ[°] | λ[°] | |
|---|---|---|---|---|---|
| 2014-01-07 | 23:10 | 887.2 | 11.3 | 0 | 88 |
For the halo CME event at 18:23 UT on Jan. 7, 2014, the resultant images obtained through the prototype program developed in this study are shown in Fig. 18. For this event period, whereas the LASCO C3 images were obtained about ten times for every 12 min during the period of 18:54 to 20:42 UT on Jan. 7, 2014, only the resulting images at 18:54, 19:18, 19:54, and 20:42 UT are shown. The CME shapes were extracted consecutively, and by analyzing the interface of the extracted CME shapes, when the CME was determined to be a halo CME, an ellipse was constructed. Consequently, the morphological parameters produced, and the basic information of the ellipse, are summarized in Table 5. In the ellipse information in Table 5, MJ indicates the length of the semi-major axis, MN represents the length of the semi-minor axis, and R is the farthest distance from the solar center on the CME interface; all values are indicated by the size of the pixel. Using the ellipse information of morphological parameters produced, a matching analysis was conducted, and as a result, the halo CMEs were determined to be from the same event. For the halo CME identified for the period of 18:54 to 20:42 UT on Jan. 7, 2014, using the morphological parameters and ellipse information, 3-D physical quantities were finally produced, and are summarized in Table 6.

| T21.5Rs | Vr [km/s] | ω[°] | λ[°] | ϕ[°] | |
|---|---|---|---|---|---|
| 2014-01-07 | 20:14 | 1,625.5 | 48.7 | 2.6 | 26.5 |
For the halo CME event at 03:38 UT on Mar. 23, 2014, the resultant images obtained from the 2013 CME analysis program are shown in Fig. 19. In Fig. 19, the CME detection results of a LASCO C3 image, SETREO A image, and STEREO B image are shown from the left. The program detected the halo CME successfully using the LASCO C3 and STEREO B images, but detected another CME using STEREO A images. Thus, incorrect 3-D physical quantities were generated, and are summarized in Table 7.
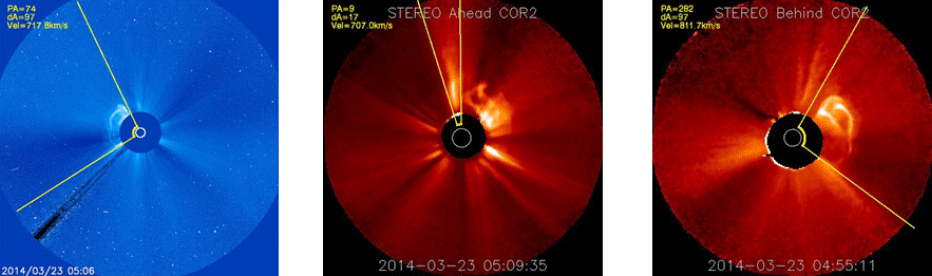
| T21.5Rs | Vr [km/s] | ω[°] | λ[°] | ϕ[°] | |
|---|---|---|---|---|---|
| 2014-03-23 | 08:01 | 874.6 | 29.6 | 53 | -18 |
For the halo CME event at 03:38 UT on Mar. 23, 2014, the resultant images obtained through the prototype program developed in this study are shown in Fig. 20. For this event period, the LASCO C3 images were obtained about four times for every 12 minutes during the period of 05:18 to 05:54 UT on Mar. 23, 2014. The CME shapes were extracted consecutively, and analyzing the interface of extracted CME shapes, they turned out to be a halo CME, and an ellipse was constructed. Finally, the produced morphological parameters and the basic information of the ellipse are summarized in Table 8. Using the ellipse information of morphological parameters produced, a matching analysis was conducted, and as a result, the halo CMEs were determined to be from the same event. For the halo CME identified for the period of 05:18 to 05:54 UT on Mar. 23, 2014, using the morphological parameters and the ellipse information, 3-D physical quantities were finally produced, and are summarized in Table 9.
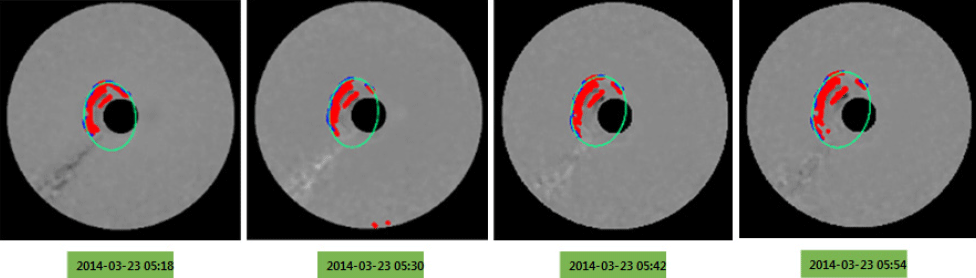
| T21.5Rs | Vr [km/s] | ω[°] | λ[°] | ϕ[°] | |
|---|---|---|---|---|---|
| 2014-03-23 | 07:42 | 841.9 | 53.6 | -8.5 | 40.4 |
For the halo CME event at 12:55 UT on Apr. 18, 2014, the resultant images obtained from the previous CME analysis program of 2013 are shown in Fig. 21. In Fig. 21, the results of a LASCO C3 image, SETREO A image, and STEREO B image are shown from the left. For this event period, whereas the program detected the halo CME successfully using the LASCO C3 and STEREO B images, it detected the angular width of the halo CME more narrowly than that identified visually using the STEREO A images. Thus, among the 3-D physical quantities, the angular width was proved to be incorrect. The generated 3-D physical quantities are summarized in Table 10.

| T21.5Rs | Vr [km/s] | ω[°] | ϕ[°] | λ[°] | |
|---|---|---|---|---|---|
| 2014-04-18 | 16:35 | 1,077.3 | 30.5 | -49 | 168 |
For the halo CME event at 12:55 UT on Apr. 18, 2014, the resultant images obtained through the prototype program developed in this study are shown in Fig. 22. For this event period, the LASCO C3 images were obtained about six times for every 12 minutes during the period of 13:54 to 15:06 UT on Apr. 18, 2014. Among these images, the images at 13:54, 14:06, 14:42, and 15:06 UT are shown. The CME shapes were extracted consecutively, and analyzing the interface of the extracted CME shapes, they were determined to be a halo CME, and an ellipse was constructed. Finally, the produced morphological parameters and the basic information of the ellipse are summarized in Table 10. Using the ellipse information of the morphological parameters produced, a matching analysis was conducted, and as a result, the halo CMEs were determined to be from the same event. For the halo CME identified for the period of 13:54 to 15:06 UT on Apr. 18, 2014, using the morphological parameters and the ellipse information, 3-D physical quantities were finally produced, and are summarized in Table 12.
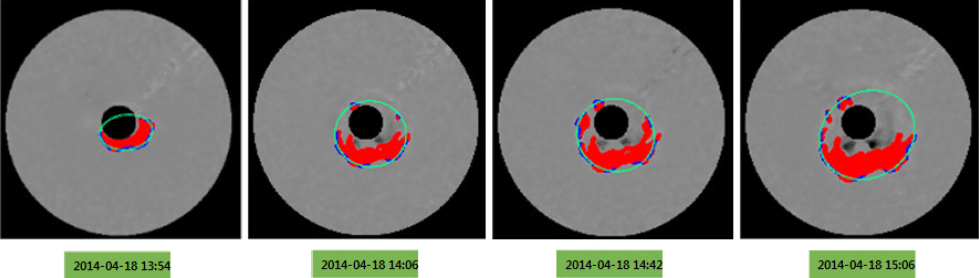
For the past three halo CME events, 3-D physical quantities were generated using both the 2013 CME analysis model program and the CAT prototype CAT. Feeding these 3-D physical quantities into the ENLIL-cone model, the arrival time of the halo CME at Earth was estimated. Table 13 shows a summary of the 3-D physical quantities of the halo CME determined by the 2013 CME analysis model program, and the arrival time at Earth determined by the ENLIL-cone model. As a result, it was estimated that all three halo CME events were unable to reach Earth.Table 11Table 12
| T21.5Rs | Vr [km/s] | ω[°] | λ[°] | ϕ[°] | |
|---|---|---|---|---|---|
| 2014-04-18 | 14:40 | 1,428.8 | 68.5 | 3.4 | 26.2 |
Table 14 shows a summary of the 3-D physical quantities of a halo CME determined by the prototype program developed in this study, and the arrival time at Earth as estimated using the ENLIL-cone model when applying the 3-D physical quantities. First, the halo CME that erupted on Jan. 7, 2014, was predicted to arrive at Earth on Jan. 10, 2014, the halo CME of Mar. 23, 2014 was estimated to arrive at Earth on Mar. 25, 2014, and the halo CME of Apr. 18, 2014, was estimated to reach Earth at 16:00 UT on Apr. 20, 2014. The actual arrival times of these three halo CME events are summarized in Table 15. The prototype program developed in this study predicted the arrival time of the halo CME at Earth more accurately than the 2013 CME analysis model program using the physical quantities produced through LASCO C3 images, the availability of which is stable.
| Reach date (Based on KSWC 3-day forecast) | |||
|---|---|---|---|
| Year | Month | Day | Time [KST] |
| 2014 | 1 | 10 | 4:30 |
| 2014 | 3 | 26 | 4:30 |
| 2014 | 4 | 20 | 20:00 |
5 CONCLUSIONS
In this study, we calculated the halo CME parameters for input into the ENLIL model, and developed an automatic CME analysis model to improve the model developed in 2013. Further, we developed an algorithm to detect and analyze halo CMEs using LASCO C3 images of the SOHO satellite, and developed an image processing technique for each stage. A validation was then conducted by inputting the resulting automatic analysis data of a halo CME into the ENLIL model.
To detect halo CMEs from LASCO C3 images, the median, smoothing, and Lee noise removal filtering techniques were applied for testing, and it was found that the median technique shows the best performance. Conclusively, the median technique was utilized to generate 3-D parameters of a halo CME. The ENLIL model inputs the speed and time when the CME reaches 21.5 Rs. Therefore, the 3-D parameter is derived by calculating the speed and time when 21.5 Rs is reached.
The previous CME analysis program developed in 2013, and the newly developed automated analysis model developed in this study, were both applied to three halo CME events of 2014, which erupted on Jan. 7, Mar. 23, and Apr. 18, the results of which were input into the ENLIL model to compare the results. Using 3-D physical quantities of a halo CME obtained from the previous CME analysis model program of 2013, it was estimated using the ENLIL model that these three events did not reach the Earth, indicating that the 3-D physical quantities were produced incorrectly. By contrast, using the results of the automated analysis model developed in this study, the ENLIL model predicted the arrival time of the three halo CMEs at Earth by 30 min, 5 hr and 30 min, and 4 hr ahead of the actual arrival times, respectively. This is a significant improvement compared to the average error of 7 hr by the ENLIL model. In addition, it was found that the automated analysis model of the current study achieved a correction of a major defect of the previous CME analysis model program developed in 2013. Because this conclusion is based on the analysis results of three halo CME events, for further study, it will be necessary to analyze more events to validate the automated analysis model, and based on the results, we will improve the accuracy of a halo CME analysis model. Furthermore, on-line service of the automated analysis model will be provided to forecast the space weather environment.










