1. INTRODUCTION
Attenuation and reflection properties of the atmosphere are often used to characterize the effect of the atmosphere on the transmission of signals through it. Low frequency waves are reflected by the ionosphere, whereas medium frequency waves are unaffected by the atmosphere and propagate without being reflected or absorbed. The various uncondensed vapors that make up the atmosphere attenuate waves at extremely high frequencies, such as radar and infrared (Singliar et al. 2004).
The theory describing the interaction between water molecules/droplets and radiation, which are seen as absorption and scattering processes, is the foundation for understanding attenuation due to rainfall. When an electromagnetic (EM) wave travels through the atmosphere, it is absorbed by atmospheric gases like H2O, CO2, O2, and O3, as well as scattered and absorbed by aerosols like haze, fog, cloud, and rain. Both events decrease the performance of all frequency sensors to some extent. Rain and gases may cause EM waves to attenuate to the point where the sensors become ineffective. Because of absorption and scattering by space particles, the quality of the radio frequency signal decreases as it travels through the atmosphere (Mandeep & Ng 2010). This decrease in signal quality has a significant impact on the information received, especially with recent advancements in satellite technology and services that demand a high data rate. Furthermore, the amount of signal loss is determined by the link, atmospheric conditions, sent signal, and receiver antenna specifications.
The issue with satellite communication is that it cannot guarantee clear communication when it rains or when the line of sight (LOS) is reduced (Oh et al. 2006). All of the major meteorological characteristics must be evaluated for a certain E-band frequency communication plan in order to create a model that aids in discovering the nearest achievable attenuation under the necessary accessible data. Researchers have created a variety of models to anticipate the attenuation induced by rain, taking into account various aspects such as geographical parameters, Earth-space link design, and the degree of atmospheric dynamics.
In the meantime, the intensity of the atmosphere’s metrological composition varies across layers. For example, places with high moisture content have high humidity, whereas places with dry surfaces have very little or no moisture content while studying the troposphere (Karmakar et al. 2010; Kestwal et al. 2014; Orji & Chiemeka 2016). Rain plays a vital role in estimating connection availability and reliability, and a smart microwave network design heavily relies on rain data from a specific location (Abrajano 2014).
Telecommunication service providers are seriously considering moving or shifting to higher frequency propagation. This is owing to the network’s high demand from C-band propagations. However, degradation impacts of rainfall and atmospheric gases on bands beyond 10 GHz are a major source of worry, particularly in tropical locations like Nigeria, where precipitation intensities are higher (Moupfouma 2009).
The standard bands of communication frequency established by the Institute of Electrical and Electronics Engineers (IEEE) are as Table 1.
| Frequency | Band |
|---|---|
| 8–12 GHz | X |
| 12–18 GHz | Ku |
| 18–27 GHz | K |
| 27–40 GHz | Ka |
| 40–75 GHz | V |
The current increase in the use of propagation wave bands is due to rapid expansion in satellite communications, decrease in the size of transceivers, and ever rising demand for bandwidth (Panagopoulos et al. 2004). To accommodate the enormous demand, radio link builders have been forced to create links employing higher frequencies in the Ku, Ka, and V bands of communication (Malinga et al. 2013). As a result, it’s distressing to see that propagations above the Ku-band (10 GHz) are severely impacted by hydrometeors (Moupfouma 1984).
The International Telecommunications Union (ITU) recommended planning for broadcasting services over 30 MHz, although the measurements used to estimate attenuation and atmospheric impacts on propagating signals are taken from satellite observations in Europe, America, and Japan (Falodun & Okeke 2013). In 1984, the ITU began an initiative for measurement of radiowave propagation in Africa, and a number of tests and operations were conducted in various parts of the continent. However, little work has been implemented in Nigeria due to the country’s lack of sufficient propagation data to plan a project (Falodun & Okeke 2013). To anticipate attenuation levels in each propagation band, this study used empirical method from the International Telecommunications Union Recommended (ITU-R) rain attenuation model. Ground-based readings from the Nigerian Meteorological Agency (NiMet) are also used to achieve this.
Rain can reduce the effectiveness of any communication and it is always more for frequencies greater than 1 GHz. In tropical countries, excessive rain has a high negative impact on communication and other wave propagation systems. In the context of communication, rain causes a Doppler frequency, which degrades signal shifting and builds in additional phase noise. The most significant degrading variables is rain. Rain degrades signals, resulting in a lot of noise at the receiver. Rain provides a scattering medium for radio signal propagation, creating signal degradation. Due to high rain attenuation in the tropics, the use of millimeter wave bands for broadband communications is limited. In tropical climates, the rate of attenuation is induced by higher rainfall and larger raindrop sizes relative to what is obtained in other climate zones of the world (Maki et al. 2001).
Rain causes significant attenuation of radio frequency radiation in the atmospheric windows at 30 and 94 GHz, however it is significantly small at 10 GHz for horizontal and vertical signal propagation (Chen 1975).
A model was provided by Chebil & Rahman (1999) for converting measured rain data from any station to its rain rate data equivalent, regardless of the available rain data’s integration time. It is calculated using a long-term annual mean accumulation, M, of rain amount for the study location, which is stated as:
where α and β are coefficients of regression defined as: α = 12.290; and β = 0.297.
The Ajayi & Ofoche (1984) model was adopted to convert rain rate from 3-minutes to 1-minute time integration values using:
where R = Rainfall rate, π = required rainfall rate time integration, T = is the available rainfall rate time integration, a and b are coefficients of integration for Rπ given as a = 1.174 and b = 0.992. The coefficient “a” may not be dependent on climate but “b” may be dependent on the climate of location or can be further investigated.
This study employs the International Telecommunications Union (ITU) model Rec. ITU-R P.530-14 in which propagation data and prediction methods required for the design of Earth-space telecommunication systems are applied ITU-R 2012). This model estimates attenuation using rain rate at a probability level of 0.01%. For other probabilities, an adjustment factor is applied to the predicted rain attenuation depth.
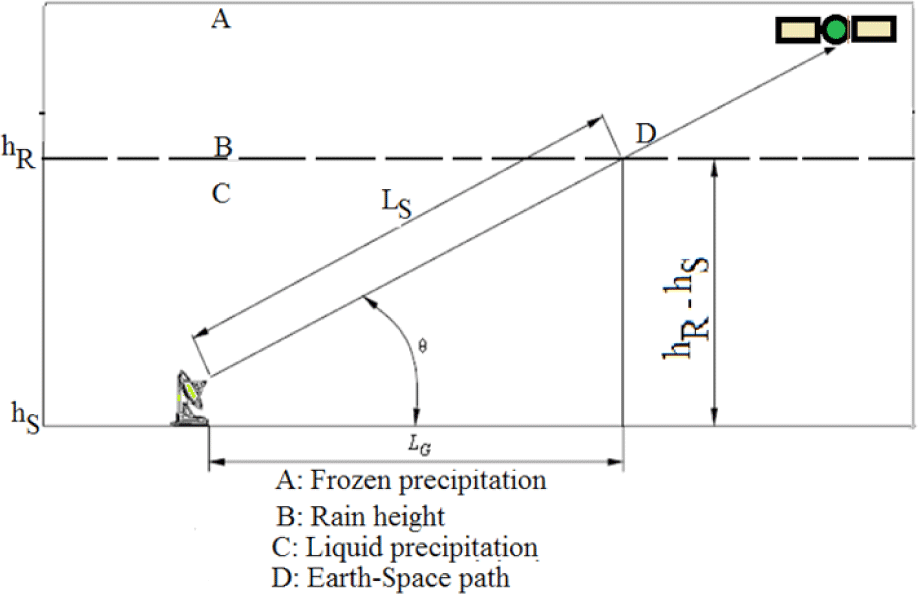
The under-listed are required to deduce the predicted rain attenuation using the model as seen in Fig 1.
R0.01: rainfall rate for the earth location for 0.01% of an average year (mm/h)
hs: height of the earth location above mean sea level (km)
θ: angle of elevation (degrees)
ϕ: latitude of the earth location (degrees)
f: frequency of propagation (GHz)
2. MATERIALS AND METHODS
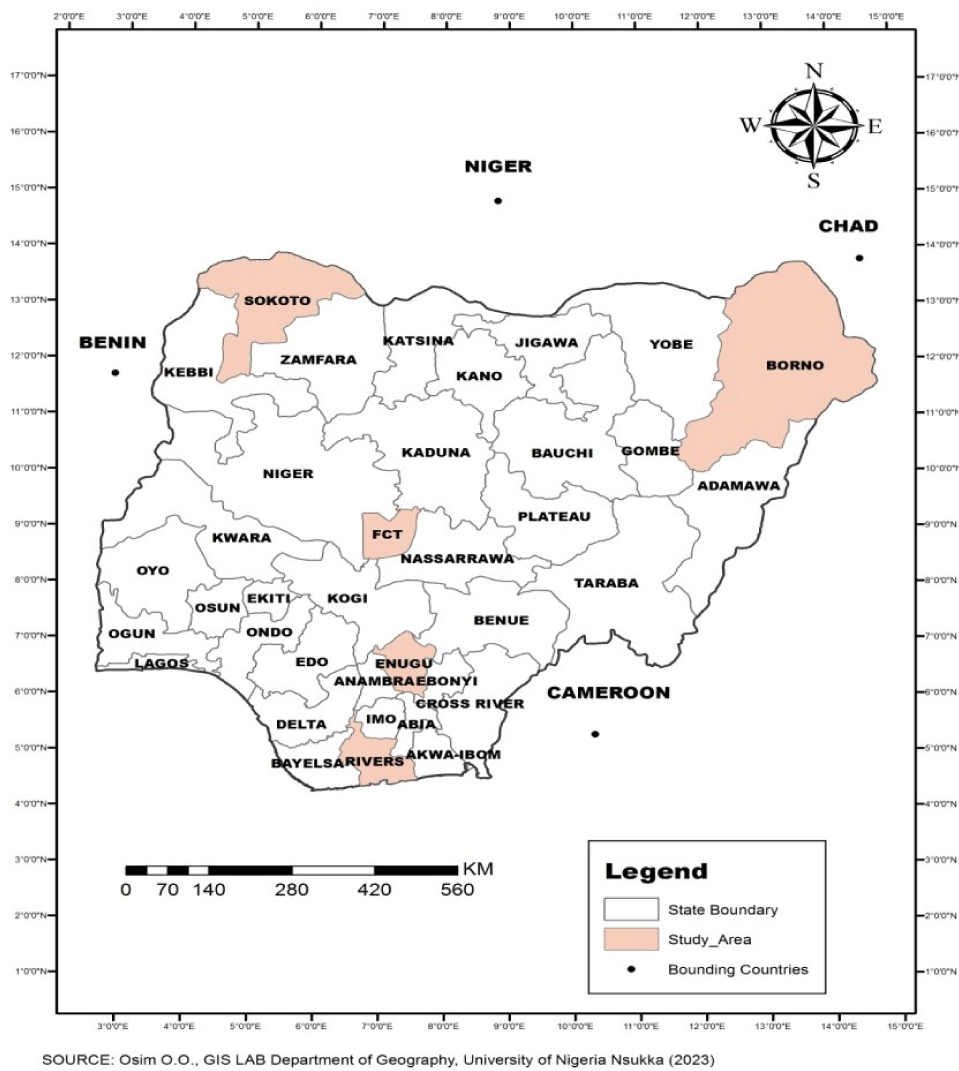
The study was carried out using meteorological data from five (5) locations. According to Köppen (1918), the classifications of Nigeria’s climate with selected locations are Maiduguri–Borno (representing the warm desert/highlands climate), Sokoto–Sokoto (representing the tropical dry/semi arid climate), Port Harcourt–Rivers (representing the tropical monsoon climate), Enugu–Enugu and FCT–Abuja (both representing the tropical savanna/wet and dry climate. The geographical locations and climatic features of the study area are shown in Table 2 and Fig. 2 respectively.
The procedure for derivation of the model and simulation is as follows:
Step 1: Deduce the rain height, hR, as presented in Recommendation ITU-R P.839:
where ho is the annual average 0°C isotherm height.
Step 2: Determine the length of rainfall slant path and the horizontal projection as:
For θ ≥ 5:
For θ < 5:
The horizontal projection is evaluated by:
Step 3: Deduce the rain rate, R0.01, at 0.01% of an average year (with 1-minute time integration) using equations (1) and (2).
Step 4: Using the polarization coefficients (frequency dependent) as stated in Recommendation ITU-R P.838 and the estimations from Step 4, deduce the specific attenuation, γR, by using:
Step 5: Estimate the horizontal reduction factor, n0.01, for 0.01% time exceedance:
Step 6: Estimate the vertical adjustment factor, m0.01, for 0.01% time exceedance:
If ζ > θ
If ζ < θ
If |ϕ| < 36°, then χ = 36 – |ϕ| (degrees)
If |ϕ| > 36°, then χ = 0 (degrees)
Step 7: The effective path length is deduced using:
Step 8: The predicted attenuation for 0.01% time exceedance of an average year is estimated using:
Step 9: The projected rain attenuation for other time exceedance (percentages) of an average year, ranging from 0.001%–5%, is deduced from the 0.01% exceedance rain attenuation for an average year:
If p ≥ 1% or |ϕ| ≥ 36°: β = 0
If p < 1% and |ϕ| < 36° and θ ≥ 25°: β = – 0.005 (|ϕ| – (36)
Otherwise: β = –0.05 (|ϕ| – 36) + 1.8 – 4.25 sin θ
3. RESULTS AND DISCUSSION
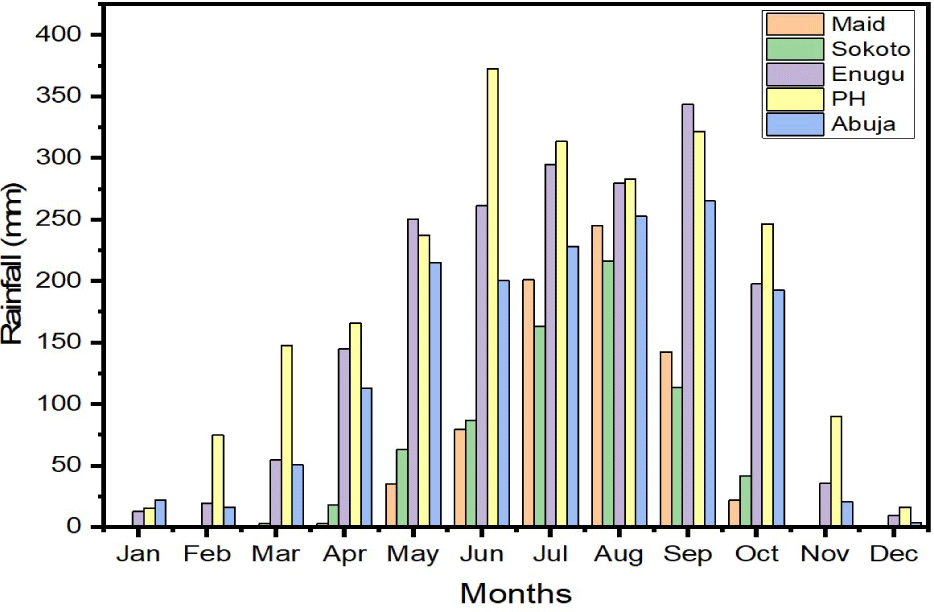
The average monthly rainfall for 10 years in the study area is shown in Fig. 3.
For the entire period, rainfall was generally low during the dry season (Nov–Mar) while the wet season (Apr–Oct) expectedly recorded higher amounts of rainfall. February was recorded as a rainy month in PH with 10 years average monthly rainfall of 75 mm. PH also continued to record maximum monthly rainfall average than the other locations except in May and September when Enugu had maximum values of 250 mm and 343 mm respectively. Also from the results of rainfall amounts in the study area, Sokoto recorded five rainy months (May–Sep) while Maidugiri recorded only four rainy months (Jun–Sep). Enugu and Abuja were observed to experience seven rainy months (Apr–Oct) while PH recorded ten rainy months (Feb–Nov) respectively as presented from the results of the 10 years average.
The months with the highest recorded rainfall represent the most adverse months for radio wave propagation in the locations within the study area (Ojo & Olurotimi 2014). The observed rainfall variation in the study area is consequent upon the climatic features of the place as recorded in Table 2. The Northern part of the country is dominated by North easterly tropical continental air mass (with dust particles moving from the Sahara desert) which results in minimum or no rain amount. Southern Nigeria experience deep moist maritime air accompanied by heavy rainfall (Ojo 1977). This accounts for maximum rainfall which dominates the location.
We shall see how these rainfall patterns affect propagated signal within the atmosphere of study area in the next presented results, showing signal attenuation due to rain at different time percentages.
The point rainfall rate estimated using the Chebil & Rahman (1999) model was simulated into the ITU-R P model to predict rain attenuation at different time percentages within the study area. The 10 years cumulative distribution of rain attenuation at these locations were then computed and analyzed, using frequencies 15, 25, and 35 GHz respectively to represent Ku, K, and Ka-band of propagation. An elevation angle of 42.5° which is the elevation angle of Nigeria Communication Satellite (NIGCOMSAT-1R) over the Atlantic Ocean region was used. The ITU-R rain attenuation model is conventionally accepted because it presents results which show that experimental data is approximately equal to the measured /actual values (Choi et al. 1997; Panchal & Joshi 2016).
The results are presented for rain attenuation at different time percentages, which include 0.001%, 0.01%, 0.05%, 0.1%, 0.5%, and 1% time exceedence. These time unavailability of signal in an average year correspond to 99.999%, 99.99%, 99.95%, 99.9%, 99.5%, and 99% respectively of signal availability in an average year. Time exceedence of 0.01% is conventionally used for simulations in the ITU-R model (Igwe et al. 2019) which corresponds to 53 minutes signal unavailability in a year.
Fig. 4 represents the prediction results of attenuation of propagated signals within the study areas. As stated earlier, the frequencies used for the study are 15, 25, and 35 GHz respectively. At a time unavailability of 0.001% (99.999% signal availability time), the entire study area is predicted to experience 15 GHz horizontally polarized signal outage. According to Ippolito (1986), most satellites operating above 10 GHz are built to withstand signal losses that are approximately ≤ 20 dB in its link because of limited carrier power at the output, transmission amplifies which is rated to be about 150 W and very low battery power used. Also, at time unavailability of 0.01% (99.99% availability of signal), Enugu, PH and Abuja are predicted to also witness signal outage because the attenuation values are more than 20 dB. Sokoto and Maidugiri are not expected to experience such outage but some severe signal dampening. For other time percentages higher than 0.01%, the predicted attenuation values are lower than 20 dB which the lowest value was recorded at time exceedence of 1%.
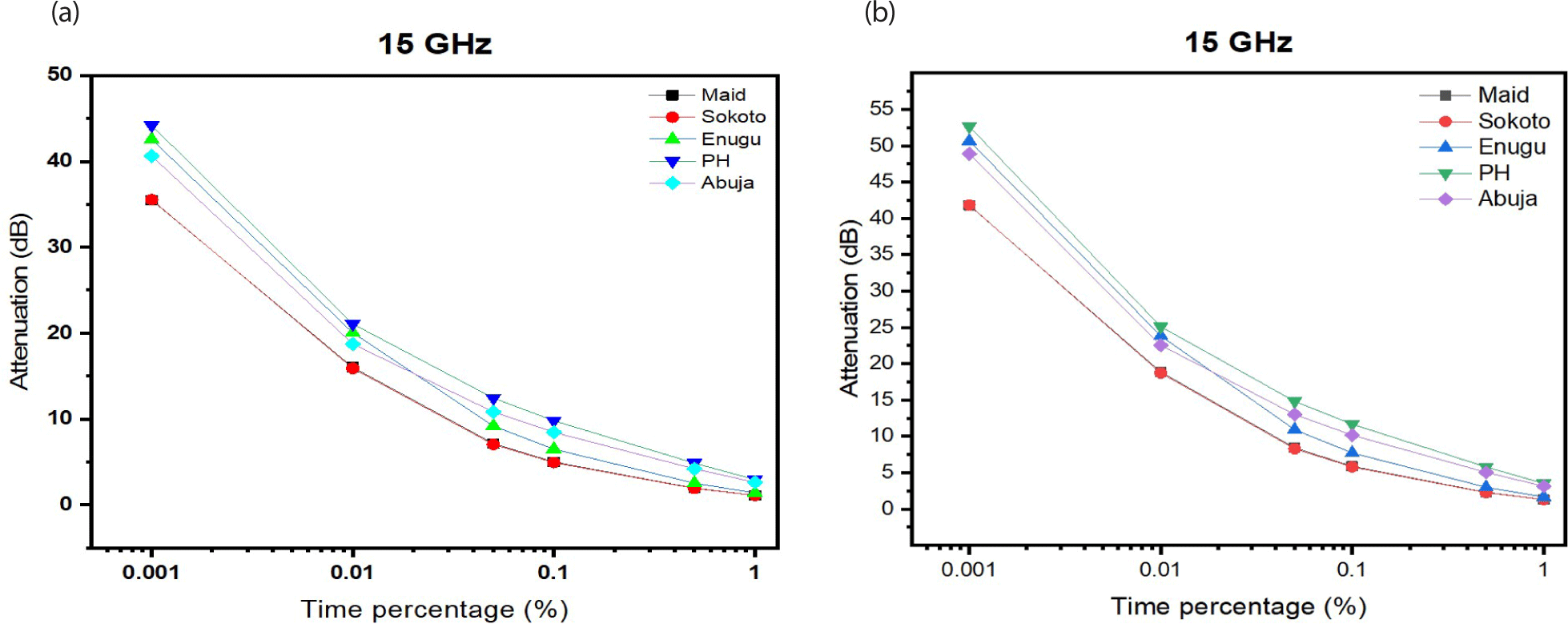
Similar results were experienced for vertically polarized signal. The five locations are predicted to experience total outage at 0.001% of time exceedence for a propagation of 15 GHz. This result is also followed by a dampening to outage at 0.01% of time exceedence predicted for Enugu and PH only. This shows that rain attenuation affects horizontally polarized signal than vertically polarized signal–water droplets and snowflakes in rain and snow are horizontally oriented, which means that they are more likely to absorb horizontally polarized microwaves (Hamad Ameen 2015; Olabisi & Oladeji 2018). The highest attenuation is experienced in PH for a horizontal propagation with a value of 53 dB for a 15 GHz signal.
As recorded in Fig. 5, the signal strength of K-band (25 GHz) propagated signal is severely dampened by rain to a maximum value of 78 dB in PH. This signal is predicted to experience total outage up to a time exceedence of 0.05% (99.95 % availability) in the area. Meanwhile, the same signal when propagated vertically was predicted to experience signal outage at only 0.001% and 0.01% of time. Above these, signal is only predicted to experience dampening but not signal outage. A horizontally polarized signal could scatter either forward or backward. Forward scattering would increase the wave’s propagation distance by 800 km. However, sideways scattering occurs peculiarly with vertically polarized propagations (Contreras et al. 2003).
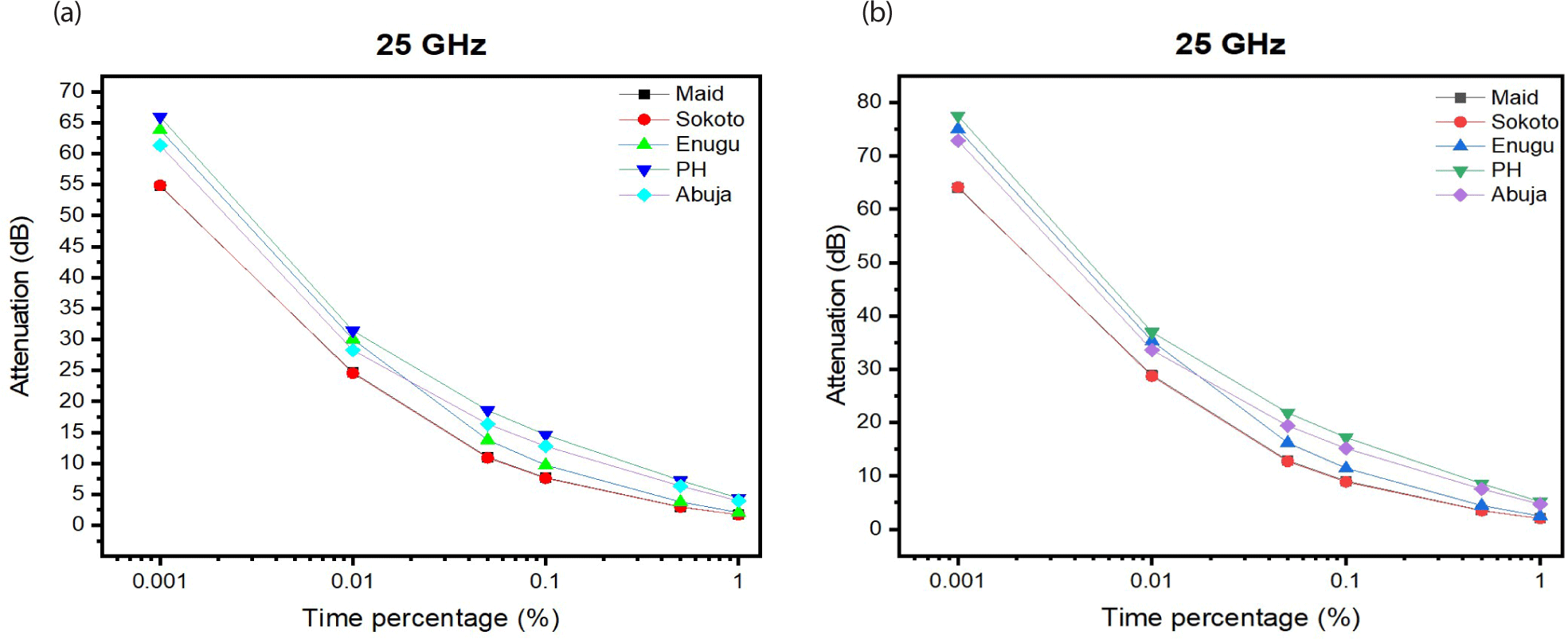
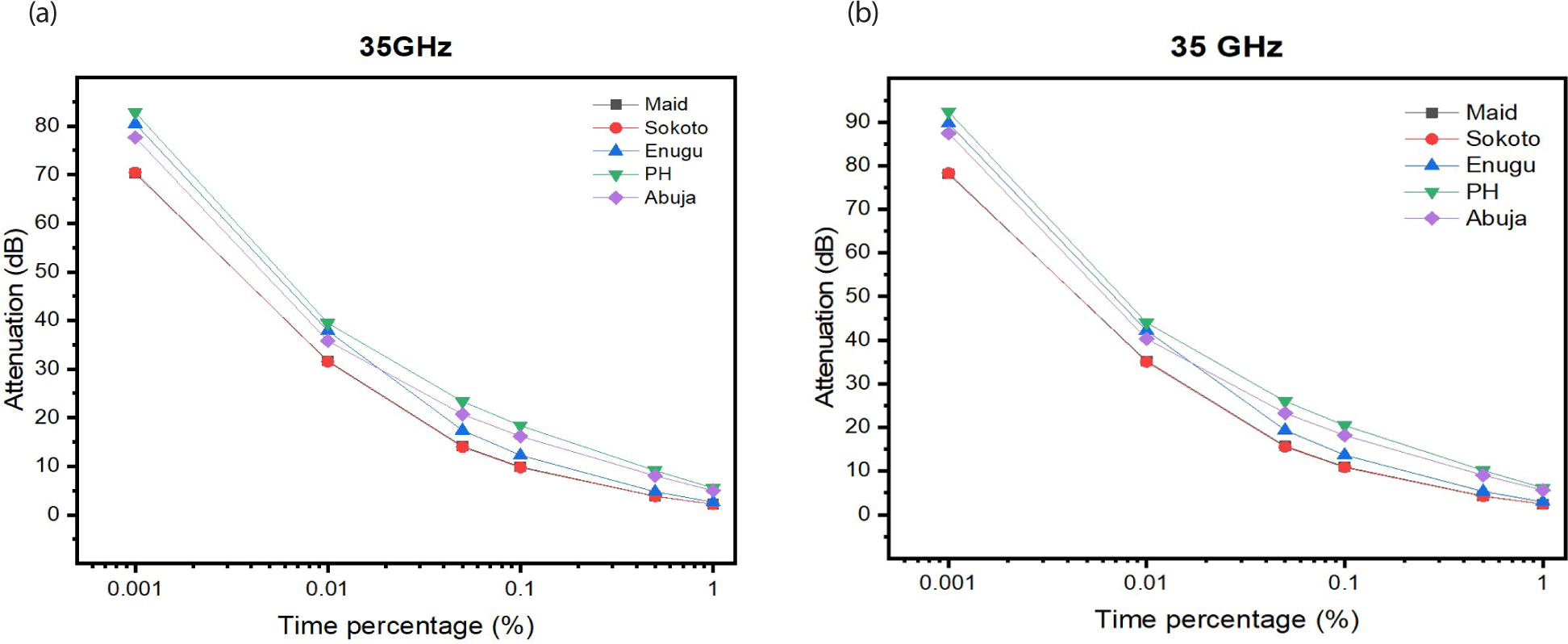
Fig. 6 shows further comparison of cumulative distribution of attenuation of Ka-band signal made at the different time percentages. Results revealed that propagated signal at times 0.001%, 0.01%, and 0.05% is predicted to experience total outage in the entire study area but would not experience total outage in Sokoto and Maidugiri at 0.05% time exceedence.
4. CONCLUSIONS
This study was on the influence of rainfall on propagated signal at different time exceedance percentages of an average year, over the climate zones of the country. Specifically, it demonstrates critical and non critical signal fade or signal outage time exceedances (0.001% to 1%) for Ku and K and Ka-band systems in an average year. The study was carried out using meteorological data made available by the NiMet over a period of 10 years (2009–2018). The four climate zones in the country were represented by five (5) locations; Maidugiri (warm desert climate), Sokoto (tropical dry climate), Port Harcourt (tropical monsoon climate), Abuja and Enugu (tropical savanna climate). The parameters were simulated into the ITU-R models for rain attenuation over the tropics and results presented using MatLab and Origin Lab.
Results of Ku band propagations showed that only locations in the tropical savanna and tropical monsoon climates experienced total signal outage for time percentage exceedances equal to or below 0.01% for both horizontal and vertical polarizations. At K band propagations, the five locations showed to have experienced signal outage at time exceedances equal to and below 0.01% while for Ka-band, there was a shift to 0.05% time exceedence for total outage to occur.
It is also observed that the bands of frequency studied experienced rain effects and possible signal power outage in all the climate zones in Nigeria, for signal availability of 99.999% (0.001% time exceedance). But for other time probabilities (0.05%, 0.1%, 0.5%, and 1%), there couldn’t have been cause for power outage alarm and dampening of signal strength was observed to be negligibly minimal. Finally, horizontally and vertically polarized signal had slightly different rain attenuation values at the studied bands for the five locations.