On the Influence of the Moment of Inertia of Gas on the Galactic Rotation Curves

1. INTRODUCTION

When it was discovered that the rotational dynamics of stars and gas on the outskirts of the galaxy did not correspond to the mass of the visible matter of the galaxy, two hypotheses were put forward to explain this phenomenon: the hypothesis of the existence of dark matter and the hypothesis of the need to modify the theory of gravity [for example, modified Newtonian dynamics (MoND) and tensor-vector-scalar theory of gravity (TeVeS)]. Such a choice of hypotheses was not accidental, as it proved itself well in the study of the solar system. Thus, to explain the anomalies in the motion of Uranus, a hypothesis was put forward about the existence of another unknown and, at the time, unobservable planet of the solar system Neptune. Later, another planet of the solar system, Pluto, was discovered by the same method. The precession of Mercury’s orbit could not be explained by the additional planet Vulcan, but it was explained by the transition from Newton’s theory of gravity to the general theory of relativity. In this regard, the hypotheses put forward to explain anomalies in the motion of stars and gas outside galaxies seem to be logical, but both of these approaches have a number of drawbacks.

Let us consider the shortcomings of the hypothesis of the existence of dark matter. On the one hand, dark matter in both elliptical and spiral galaxies is distributed spherically and symmetrically, that is, regardless of the distribution of visible matter. The spherical distribution of dark matter is proved by the existence of the galaxies NGC 2685, NGC 4650A, A 0136-0801, and ESO 415-G26 (Schweizer et al. 1983) of a gas polar ring located at a distance of three radii of the stellar disk and rotating in a plane perpendicular to the stellar disk. On the other hand, the rotation speed of the ring corresponds to the velocity of the boundary of the stellar disk, which means that the masses of dark and visible matter correlate with each other in a certain way (McGaugh et al. 2016). To date, this contradiction has not been resolved within the framework of the hypothesis of the existence of dark matter.

Secondly, there is the MDAR (Mass Discrepancy-Acceleration Relation) problem, which defines the dominant role in determining accelerations in any galaxies for visible matter. Thus, the study of the movement of 400 stars at distances up to 13,000 light-years from the Sun did not reveal the influence of dark matter (Bidin et al. 2012), from which it could be concluded that there is no dark matter inside the galactic disk. The same conclusion follows from the Tully- Fisher relation (Verheijen 2001), according to which the luminosity of the galaxy, proportional to the mass, ideally correlates with the speed of its rotation. That is, within the framework of the dark matter hypothesis, it remains unclear why the more massive dark matter remains outside the galactic disk and does not collapse into the galactic disk.

Other models include the work (Farnes 2018), in which the authors combine dark matter and dark energy into one phenomenon – an ideal liquid with a negative mass. But this model today has a small calculation base and is also not confirmed experimentally in everything. In (Babourova et al. 2018), the Weyl-Dirac conformal theory of gravity is considered, which is Cartan-Weyl space-time gravitation theory with a Dirac scalar field to model dark matter. However, like in other theories with scalar fields, there remains an essential problem of detecting such scalar fields.

Let us consider the shortcomings of hypotheses about modified theories of gravity. Currently, there are two theories according to which the physical nature of gravity changes on large scales: MoND and TeVeS (Milgrom 2011). MOND cannot explain gravitational lensing, nor can it explain the discrepancy in the calculations of the center of mass of a system of colliding galaxies in their mutual motion and in the radiation of visible matter (Milgrom 2011). The shortcomings of TeVeS include the incapability of simultaneously explaining cosmic microwave background anisotropy and structure formation. It is also shown in (Jain et al. 2013) that some effects predicted by TeVeS are not confirmed within the accuracy of measurements. In addition, both MoND and TeVeS theories cannot explain the absence of the dark matter effect in two ultradiffusive galaxies (Cohen et al. 2018;van Dokkum et al. 2018).

These problems identified in the main hypotheses need to be addressed.

2. METHODS

In Newtonian mechanics, equations describing translational and rotational motion are similar in their form. This evokes the notion of a certain symmetry between translational and rotational motion. However the theory of relativity disrupts this symmetry. So in the theory of relativity, inertial translational motion is determined by a geodesic plotted in four-dimensional space-time, while the inertial rotational movement uses a vector of angular velocity which only moves along the geodesic. Our past studies (Portnov 2015;Portnov 2018;Portnov 2021) provided arguments for restoring the symmetry between translational and rotational motion. To that end in (Portnov 2015;Portnov 2018;Portnov 2021) we introduced the concept of a sevendimensional phase space-time where inertial translational and rotational movement would be represented by a curve that is the geodesic for the metric of the particular phase space-time. Thus the equations for translational and rotational movement alike are determined by the principle of least action. However, if curved phase space-time is considered, complete symmetry between translational and rotational motion could not be attained. The next step toward achieving symmetry between translational and rotational motion was taken in (Portnov 2022). It is known that inert mass used in translational motion has an equivalent gravitational mass. So it was hypothesized in (Portnov 2022) that the moment of inertia as a measure of inertia in rotational motion would similarly have a corresponding equivalent gravitational moment of inertia. With that in mind, the force of gravitational interaction with a point mass $m$ is determined by the equation:

where M and J are the gravitational mass and moment of inertia of the body that generates the gravitational field, G is Newton’s gravitational constant; D is some new constant of interaction, R is a distance from the body that generates the gravitational field to the point mass m. Using Eq. (1), we obtain the equation of the orbital velocity of the point mass for stable orbital motion:

It should be noted that visible matter exists beyond the boundaries of the galactic disc. It is comprised by accumulated gases such as atomic hydrogen HI and molecular hydrogen H₂ whose presence can be detected in the X-ray band (Thean et al. 1997;Battaglia et al. 2006;Vikhlinin et al. 2006). But the surface luminosity of gas, and hence its mass, is not enough to account for the velocities of gas and star motion outside of the stellar disc. Yet the gas, due to its extensive dimensions, has a significant moment of inertia which, according to Eq. (1), can influence motion velocities of test bodies in an essential manner. In support of the hypothesis positing the existence of a gravitational moment of inertia, velocity curves are computed in (Portnov 2022) for three spiral galaxies. It is shown that the use of Eq. (2) for the computation of galaxy velocity curves agrees well with observed values. There is a number of weak points in (Portnov 2022) as rotation velocities are validated over a rather narrow sample in galaxies and a multitude of parameters are left free. To illustrate, six free parameters were introduced for simulating the density of a galaxy’s stellar disc and gas densities. Five parameters would be necessary to bring the model of mass distribution in a galaxy into alignment with observed data on the latter’s luminosity. Another free parameter was the interaction constant D.

3. RESULTS

In this study we will test our hypothesis by computing rotation velocity curves for fourteen galaxies as we reduce the number of the parameters. With that goal in mind, our method for computing moments of inertia relies on a known distribution of masses of the stellar bulge, the stellar disc and gas. Table 1 summarizes the parameters of galaxies in the sample.

The distribution of mass in the bulge of the galaxy M_b(R), in the disk of the galaxy M_d(R) and gas M_g(R) is taken from (Begeman 1989;Corbelli & Salucci 2000;Freese 2009;Doroshkevich et al. 2012;Haghi et al. 2016). Using the gas mass distribution, we calculate the gas density distribution:

The distribution of the moment of inertia for the stellar bulge and the disk was found by splitting the stellar bulge and the disk into 2ΔR thick layers with the moments of inertia:

where m_i, R_i is the mass and distance from the center of the galaxy of the i star, R_k is the distance from the center of the galaxy to the middle of the 2ΔR thick layer, α is some constant reflecting the distribution of stars in the galactic disk. Note that in this equation, the masses of only such stars are considered, the distances R_i to which lie in the interval R_k – ΔR ≤ R_i ≤ R_k + ΔR. Then, the total moment of inertia of the stellar bulge and the disk with radius R is found as:

The moment of inertia for gas due to its spherically symmetric distribution around the galaxy will be sought as an integral over all moments of inertia of spherical layers $d{J}_g\left(r\right)=\frac{2}{3}{r}^{2}d{m}_g$:

In this paper, the integral of the moment of inertia of gas will be found by the method of Riemann sum. Then, using Eq. (2), we find the orbital velocity of the point mass:

In the numerical simulation of velocities, two free parameters D and α were selected in this way (Table 2) so that the obtained velocity value coincides with the observed values (Begeman 1989;Corbelli & Salucci 2000;Freese 2009;Doroshkevich et al. 2012;Haghi et al. 2016). It is interesting to note here that the parameter α = 1 was obtained for an irregular galaxy, while for spiral galaxies it is less than one. The calculated velocities for galaxies are summarized in Tables 3–16. The graphs in Figs. 1–3 show the observational velocity curves (Begeman 1989;Corbelli & Salucci 2000;Freese 2009;Doroshkevich et al. 2012;Haghi et al. 2016) and the velocity curves calculated in the model under discussion (Tables 3–16).

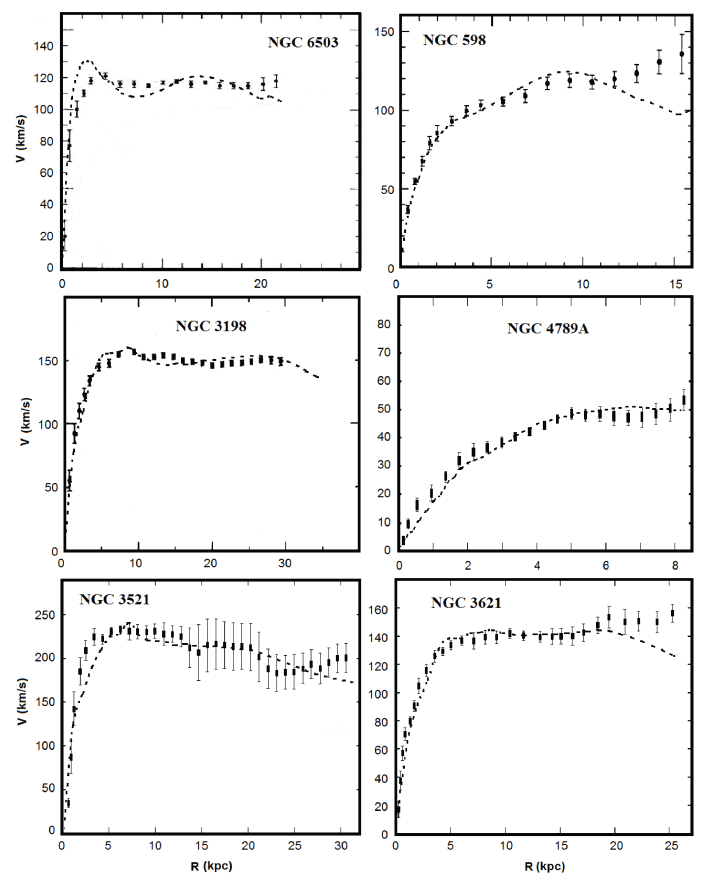
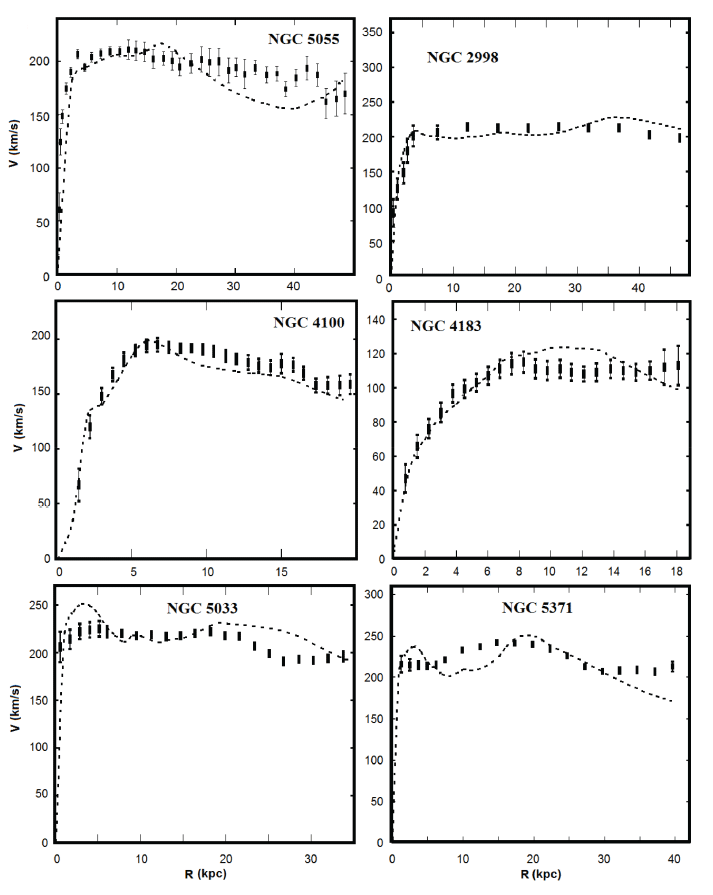
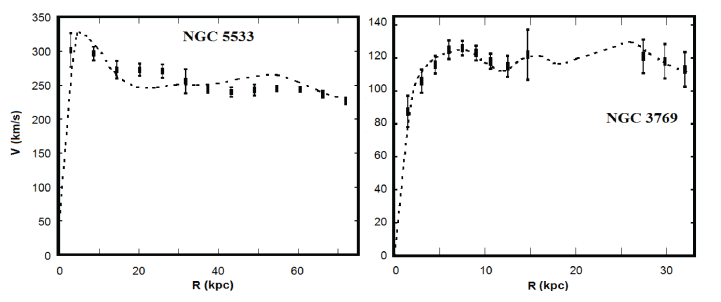
As can be seen from Tables 3–16, inside the galactic disk, the moment of inertia of gas J_g and the moment of inertia of the disk J_d or bulge + disk J_b+_d are very small, this explains the fact that there is no noticeable deviation of the stellar movement dynamics from the distribution of the mass of visible matter inside the galactic disk. Outside the galactic disk, the moment of inertia of gas J_g begins to increase sharply, therefore, the term with the moment of inertia begins to prevail in Eq. (1); this fact circumstance explains why the motion dynamics of test bodies outside the galactic disk differs from the distribution of the mass of visible matter.

As can be seen from the graphs shown in Figs. 1–3, the velocity curves obtained based on the calculations of the model under discussion are comparable in order of magnitude with the observed velocity curves of the rotation of galaxies. The existing discrepancies between the model curve and the observation curve can be caused by errors accumulated during numerical modeling and errors in determining the volume densities of gas. Note that such a coincidence is obtained with no dark matter involved. In this case, the magnitude of the interaction constant D for all galaxies coincides in order of magnitude (Table 2).

Summarizing the found interaction constants D for all galaxies (Table 2), we find the average interaction constant:

Despite the fact that the methods for calculating the velocities in this paper and in (Portnov 2022) are different, the obtained values of the interaction constants D are the same in both papers.

Due to the small value of the interaction constant D and the peculiarity of Eq. (1), on the scale of the solar system for point bodies (the Sun, planets, and small bodies), the contribution of the moment of inertia J due to gravitational interaction will be insignificant, compared to the mass contribution M.

On the galactic scale, the moment of inertia for gas extended in space will be large, so the contribution of the moment of inertia due to the gravitational interaction Eq. (1) becomes predominant, which manifests itself in a higher motion velocity of test bodies outside the galaxy than can be expected from the mass alone.

Separately, we note that due to the influence of the moment of inertia on the gravitational interaction force, the center of mass, determined by the gravitational field of the galaxy, and the center of mass, determined by the apparent distribution of mass in the galaxy, may not coincide. A similar situation may arise when galaxies collide, due to the redistribution of gas around colliding galaxies, the moment of inertia will change, and the gravitational center of mass determined by it will change, too. This may explain why the gravitational center of mass of colliding galaxies does not coincide with the center of mass determined by the distribution of visible matter. The model described herein can be verified by comparing the coordinates of the center of mass of colliding galaxies, calculated from the distribution of gas and from the motion dynamics of the galaxies.

4. CONCLUSION

Summing up, we note that the article has being studied a model to explain the rotation curves of galaxies without involving dark matter. The force created only by the mass of luminous matter cannot explain the shape of the rotation velocity curve. But if we assume that the moment of inertia of gas outside the galaxies also creates a gravitational field, then the rotation curve of the galaxies can be easily explained. At the same time, as shown in the paper, shapes of the observed and modelled rotation curves correlate in order of magnitude. It is also shown that the moment of inertia of gas inside the stellar disk is too small to significantly affect the rotational dynamics of the test bodies, which explains why the rotational dynamics of stars inside the galactic disk is completely explained by the stellar mass.

Using numerical simulation based on data from fourteen galaxies, the constant of gravitational interaction caused by the moment of inertia was found D. The very small value of the constant D makes it possible to explain the absence of the moment of inertia influence on the gravitational interaction on the scale of the solar system.

In addition, the hypothesis under discussion about the influence of the moment of inertia of a weakly massive, but spatially extended gas on the gravitational potential of the galaxy can explain the lack of coincidence of the center of mass of colliding galaxies, calculated from the distribution of stars and the dynamic motion of the galaxies themselves.

We also pay attention to two ultradiffusive galaxies NGC 1052-DF2 and NGC1052-DF4, in which there is a very little or completely no dark matter (Cohen et al. 2018;van Dokkum et al. 2018). As follows from the proposed model, the rotation curves of galaxies are explained by the moment of inertia created by gas. Therefore, for ultradiffusive galaxies, which have no gas outside the stellar disk, there is no moment of inertia, which could create an additional gravitational field. That is, the being studied a model naturally explains the absence of dark matter for ultradiffusive galaxies, which is not possible in the theories of MoND and TeVeS.

The study of ultradiffusive galaxies and the comparison of their rotation curves with those in galaxies with a high content of gas lying outside the galactic disks will allow for concluding that the proposed model is reliable.