1. INTRODUCTION
Starting from the launch of the Korea Pathfinder Lunar Orbiter (KPLO), activities with Korea’s space exploration are expected to be more accelerated. The KPLO is Korea’s first space exploration mission beyond the Earth’s orbit and will be launched by a Space-X Falcon-9 launch vehicle with an expected launch period from late July to early September 2022. The final mission orbit around the Moon for the KPLO will have 90 deg of inclination with respect to the lunar equator with an altitude of approximately 100 ± 30 km throughout the one year of the mission lifetime. To secure more fuels to KPLO, the transfer method to reach the Moon for KPLO has recently changed from 3.5 phasing loop to Weak Stability Boundary (WSB) / Ballistic Lunar Transfer (BLT). There were numerous trial errors in the design phase as well as the development process of the KPLO mission, and this is expected to serve as a foundation in preparing the future of Korea’s space exploration missions. For the very recent progress on various KPLO trajectory design and analysis, the reader may refer to references (Kim & Song 2019;Bae et al. 2020;Hong et al. 2020;Kim et al. 2020a;Kim et al. 2020b;Lee et al. 2020;Park et al. 2020;Song et al. 2020).
After completion of the KPLO mission, Korea plans to focus on lunar surface investigations using landers and rovers by the end of 2030, and landing on asteroids is seriously considered by the end of 2035. Nowadays, Korea has just begun to consider another new deep space program, visiting the Apophis during its close approach to the Earth in 2029. Meanwhile, the development of Korea Space Launch Vehicle–II (KSLV-II) is making progress and its first test flight is planned for Oct. 2021 from NARO space center which is Korea’s first space center located in the southern part of the Korean peninsula. Besides launching Low Earth Orbit (LEO) satellites using KSLV-II, a way to carry out more deep space explorations using KSLV-II is now also being considered. However, due to the limits on KSLV-II performances, a small-sized spacecraft, namely with less delta-V requirement to perform the entire mission, will much be more preferable to conduct a deep space mission from NARO Space Center.
Among the various types of deep space missions: exploring planets, asteroids, etc., authors believe that missions to the near Earth-Sun Lagrange points could be another good candidate to be launched from NARO Space Center. This is because missions near the Earth-Sun Lagrange points from NARO Space Center are expected to be less affected by the launch geometry than other deep space missions that have specific target bodies. It is well known that there exist five special points in space where the gravitational forces of the two massive bodies, such as the Sun and the Earth or the Earth and the Moon, and the centripetal force balance each other. Each of the five points usually labeled from L1 to L5. Among the five points, most missions have utilized or plan to utilize L1 or L2 points which are unstable points that lie along the lines between two massive bodies. For the missions near the Sun-Earth L1 point, there are lots of benefits to performing solar physics experiments near the L1 point. Missions near the L1 point provide useful geometries for solar physics experiments such as a continuous link to Earth, constant thermal and power generation environment for the spacecraft, and most importantly, continuous viewing of the Sun while measuring the solar wind from the outside of the geo-magnetosphere. Similarly, the location of L2 is suitable to measure the geotail with its interaction with the solar wind and also provides the perfect environment for astrophysics experiments such as a stable and cold environment suited for infrared and microwave space telescopes (Lo 1997). For these reasons, there were numerous missions conducted or planned in the vicinity of L1 or L2. The first mission that utilized Lagrange point was the International Sun-Earth Explorer (ISEE-3) launched in 1978 toward L1 (Farquhar et al. 1980). Additional missions that have also been launched near the L1 point are Solar and Heliospheric Observatory (SOHO) (Stalos et al. 1993), Wind (Sharer et al. 1992), The Advanced Composition Explorer (ACE) (Stone et al. 1998), Genesis (Lo et al. 1998) and The Deep Space Climate Observatory (DSCOVR) (Roberts et al. 2015). Other than these missions, the Microwave Anisotropy Probe (MAP) (Bennett et al. 2003), the James Webb Space Telescope (JWST) (Dichmann et al. 2014), and many other missions were flown to the L2 region of the Earth-Sun Lagrange point.
Authors strongly believe such missions, near the vicinity of the Sun-Earth Lagrange points, could be another options for the future of Korea’s deep-space missions. In fact, as described above, missions around the L1 region provide great opportunities to study solar physics and the L2 region mission is suitable for space telescope for deep space observation. If these missions are realized using KLSV at the NARO Space Center, it can be not only a great opportunity for Korea to contribute greatly to the international space science community using relatively small sized satellites, which is currently the trend of space exploration, but also the utilization of the KSLV can be maximized. Therefore, the current work is conducted to find out the early feasibilities of the Sun-Earth Lagrange point missions launched from NARO space center. Unlike common approaches that uses Circular Restricted Three-Body Problem (CR3BP) for preliminary design and analysis purposes, the current work applied multi-body dynamics to formulate given Lagrange point mission from the beginning. The current work also considered the location of the NARO Space Center as a starting point as to eliminate the problem of patching the trajectory solutions later, which require another set of iteration to screen the appropriate launch opportunities from the NARO Space Center. It is a very common and time consuming procedure if the preliminary trajectory design problem was solved under CR3BP without consideration of the launch site location. Consequently, the current approach can save a lot of time and effort for the mission designer who has to applicate and furthermore, complete the real-world mission design and analysis. The research described in this paper is conducted under many assumptions that need to be resolved and matured in order to be fully applied to the real-world mission, nevertheless, results from the current work can provide many insights into the relevant communities and are expected to be used as a good starting point to establish national long-term plans to include such a mission.
The remainder of this manuscript is organized as follows. In Section 2, a detailed targeting method used to formulate the Sun-Earth Lagrange point is presented. Numerical implications used such as the high fidelity dynamic model applied in the current work is discussed in Section 3 together with assumptions made for the simulation. Section 4 provided simulation and analysis results including launch opportunities as well as examples of Lagrange Orbit Insertion (LOI) and Orbit Maintenance (OM) maneuver design results. For launch opportunity analysis, the current work provided characteristic on launch injection energy per unit mass (C3), Right ascension of the injection orbit Apoapsis Vector (RAV), and Declination of the injection orbit Apoapsis Vector (DAV) for each Target Interface Point (TIP) of a different launch date. Characteristics of Trans Lagrange Cruise (TLC) trajectory with daily launch windows (based on features of coasting arc) from the NARO Space Center are also analyzed and discussed. Finally, the conclusions are presented in Section 5. The results of this study will be of great help in determining the feasibility of performing deep space exploration missions using the NARO Space Center. In particular, the characteristics of the TIP parameters and coasting arcs presented in this study will contribute greatly if and when the proposed mission is realized more specifically. Especially, establishing the initial requirements of the launch vehicle performance, sizing of the spacecraft bus system, and further establishment of initial operational concept, etc.
2. TARGETING PROBLEM FORMULATION
In general, the Lagrange point targeting problem can be constructed in a straightforward manner under the wellknown CR3BP. However, conic arc approximations are usually used with CR3BP, and therefore, obtained solutions have to be corrected with a precise ephemeris and highfidelity dynamics model to applicate obtained solutions to the real-world mission. As the trajectory design of the Sun- Earth Lagrange environments is very challenging, due to complex multi-body dynamics, several innovative trajectory design tools are developed to support design and operation activities for the Lagrange point mission (Folta et al. 2016).
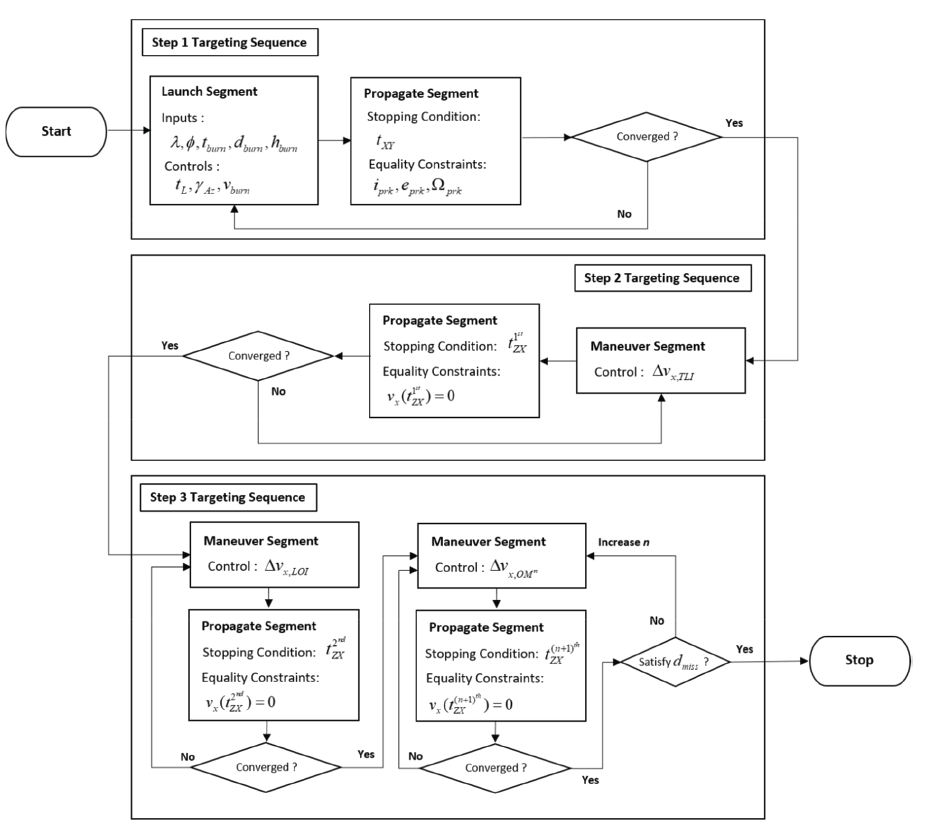
Among the several trajectory design tools, this research utilized System Tool Kit (STK) Astrogator by Analytical Graphics (AGI) to numerically target L1 and L2 transfer and orbiting problems. The Astrogator is an add-in module of the STK, and trajectory or orbit targeting problems can easily be designed and formulated using a Mission Control Sequence (MCS) inside of the Astrogator. The Astrogator has been used to design and operate not only many Earth missions but also non-Earth based ones including the Sun- Earth Lagrange point missions such as Wind, SOHO, ACE, and MAP, etc. (Carrico & Fletcher 2002). With the utilization of STK Astrogator, the trajectory design problem of near the Sun-Earth Lagrange environments can easily be formulated and interpreted under a high-fidelity dynamics model. The current targeting problem includes the following three different mission phases to complete the overall Lagrange mission. Those three mission phases are: launch from NARO Space Center, transfer to the vicinity of the Lagrange point, and finally insertion into the vicinity of the L1 or L2 and orbiting around them. To implement all three mission phases, launch, propagate, and maneuver segments are appropriately nested to formulate a targeting sequence inside of MCS. To complete the entire MCS, step-by-step targeting sequences are formulated as follows.
For the first step, the launch segment is used to consider the location of NARO Space Center and the KSLV-II is assumed as a launch vehicle to deliver the fictitious spacecraft into the L1 or L2 orbit. The main purpose of this first targeting sequence is to find the appropriate TIP to perform Trans Lagrange Injection (TLI) burn that meets the parking orbit constraints. The launch segment used the following parameters as input: longitude and latitude of NARO Space Center, λ and ϕ, launch epoch, tL, at NARO Space Center. For burnout parameters of the KSLV-II, time of flight, tburn, launch azimuth, γAz, downrange distance, dburn, altitude, hburn, and burn out fixed velocity, υburn, are considered. To nest equality constraints at the time of TIP, tTIP, the Sun-Earth Rotating (SER) frame was defined with the following unit vector definition. The unit vector of the x-axis of defined SER frame points along the vector between the Sun and the Earth/Moon barycenter, the z-axis points along the angular momentum vector, namely always perpendicular to the ecliptic plane, and finally, the y-axis is defined as to complete the right-handed system. With the control parameters of tL, γAz, and υburn, the states are propagated until (either decreasing or increasing dependent on target geometry) to cross XY plane, tXY, of defined in the Earth-centered SER frame and this tXY would be the best tTIP in orbital geometry point of views. Finally, the eccentricity, eprk, the inclination, iprk, and right ascension angle, Ωprk, of the parking orbit at tXY are given as equality constraints that need to be met. Here, Ωprk is defined in the Earth-centered SER frame, and other constraints, namely eprk and iprk, are defined in the Earth-centered the International Celestial Reference Frame (ICRF) frame. With constraining Ωprk to 0 deg, the geometry of the TIP for TLI burn can always be achieved to lie within Sun or anti-Sun vector direction. Here, readers must note that the actual tTLI does not exactly matches to the tTIP, however, it is assumed tTIP = tTLI as imparted TLI burn is assumed as to be impulsive.
Once Step 1 is completed, the second targeting sequence is initiated. The main purpose of step 2 is to achieve an appropriate TLC trajectory. In Step 2, the x component of the TLI burn vector, , is controlled and states are propagated until the time when the spacecraft intercepts the ZX plane of the Earth-centered SER frame, , for the first time. Here, the TLI burn vector is defined in the Earthcentered Velocity – Normal – Co-normal (VNC) frame. In the VNC frame, the unit x-axis is defined as along the velocity vector, the unit y-axis is along the orbit normal and the unit z-axis completes the orthogonal triad. Therefore, the x component of TLI burn is always imparted along the velocity direction. For the final terminal constraint, the x component of the velocity vector, υx, in the Earth-centered SER frame at is constrained as to always be zero. The equality constraint of ensures a perpendicular ZX plane crossing which indicates the energy balance of the spacecraft, not to fall back in either the Sun or the Earth direction (Roberts et al. 2015). Readers may note here that equality constraints at may be strongly dependent on final aiming orbits, namely, the sub-classes of Lissajous orbits. The current work only considered constraint of which leads the target orbit to be a Lissajous orbit rather than a halo orbit around the Lagrange point. Also, only the direct transfer option to the vicinity of the Lagrange point is considered in this work, and other transfer methods such as the utilization of phasing loop orbits or the lunar flyby to reach the Sun-Earth L1 or L2 points are not considered. During the TLC phase, several statistical Trajectory Correction Maneuvers (TCMs) can be placed to correct errors induced from TLI burn, orbit determination (OD), and many other sources before inserting the spacecraft into the orbit around the Lagrange points. As the total numbers, locations, as well as magnitudes of allowable TCMs are so mission-specific the current work did not consider any TCMs during the TLC phase and relevant work has remained as another analysis topic for upcoming research.
The spacecraft will intercept the ZX plane at and will perform the LOI maneuver to insert the spacecraft into its intended mission orbit around L1 or L2. After the successful insertion, the spacecraft will perform OM maneuvers to keep the spacecraft from falling back to the vicinity of Earth or into a heliocentric orbit around the Sun by maintaining its orbital energy. In Step 3, the final mission orbit around L1 or L2 is established via the execution of the LOI and OM maneuvers. Firstly, the x component of the LOI burn, Δυx,LOI, is controlled and propagated until the 2nd ZX plane crossing, , in Earth-centered SER frame to meet the constraints of . Unlike , the LOI burn vector is defined in the Earth centered SER frame as to ensure imparted velocity change is along the velocity vector. The targeting problem of OM maneuver is formulated very similar to that of LOI burn targeting strategy in this work. The x component of series of OM burns, x ,OMn Δv , is controlled and propagated until nth+1 ZX plane crossing, (n 1)th ZX t + , in the Earth-centered SER frame to meet the constraints of ( ( 1) ) 0 n th x ZX v t + = , where n is the number of OM maneuvers, from 1 to N, needed to meet the overall mission duration, dmiss, the requirement of which is one year for this work. The magnitude of the LOI maneuver is strongly dependent on the size or the orientation of the targeting mission orbit, i.e., 3-dimensional amplitudes for Lagrange points. Again, the size or the orientation of the target mission orbit is strongly dependent on the mission objectives: in the case the science goal of the mission. Similarly, the OM strategy is strongly dependent on the detailed mission objectives and from these mission objectives, various mission constraints will be flow downed and a total number and various size of OM maneuvers will be required to meet the constraints. Other than OM maneuver, another set of maneuvers can also be suggested to meet those of mission-derived constraints, i.e., extra delta-V’s to maintain axis constraints. As a detailed mission objective has not been established for this work, the current work adopted a very simple LOI and OM strategy which is focused to just make the spacecraft orbit around the Lagrange points. No further detailed constraints are considered which are likely to be considered in real-world trajectory design work such as detailed limits on maintaining science altitude, maneuver execution direction constraints, propulsion system limits, i.e. size and duration, Solar Exclusion Zone (SEZ) avoidance, net delta-Vs induced from attitude control of the spacecraft, ground visibility conditions, thermal and space radiation conditions, etc. Control strategies to keep the spacecraft in the vicinity of the Lagrange points is another area of research and readers can find extensive literature on those topics. In Fig. 1, the overall targeting sequence formulated to establish the given problem is depicted.
3. SIMULATION SETUP AND ASSUMPTIONS
A high fidelity dynamics model is used to formulate the current Sun-Earth L1 and L2 point orbiting mission. The applied high fidelity dynamics model includes the 3rd body effect of the Sun, Earth, and Moon with the ephemeris source of DE430. For the phase when the spacecraft is near the vicinity of the Earth, the Earth’s gravitational field model is additionally considered with the EGM2008 gravity model, and the effect of atmospheric effect is also considered with the Jacchia-Roberts density model. Solar radiation pressure is considered with the spherical shape of the spacecraft with dual cone shadow model, and the Earth and the Moon are considered as the eclipsing bodies. For the numerical integrator, the RK7-8th integrator is used with variable step size control that controls the errors relative to states. A differential corrector with Singular Value Decomposition (SVD) method is used to solve the targeting problem shown in the previous section and the Secant method with applying forward difference derivative calculation method is used for the root-finding method. The candidate launch year is assumed as 2030 with the location of NARO space center at λ = 127.536 deg East and ϕ = 34.432 deg North. For the performance of KSLV-II the following assumptions are used as a fixed value. tburn = 850 sec, hburn = 300 km and dburn = 3,700 km. These are only assumptions and may differ for real flight performances of KSLV-II, and therefore, the results provided in this work may change and will be revised and updated until the last minute when every mission parameter is clear. This iteration process is very common in real-world trajectory design and analysis activities. eprk is assumed 0 and iprk = 80 deg to regard the location of the NARO space center and finally, the launch year is assumed to be 2030. In the following section, simulation, as well as analysis results, will be discussed with assumptions made previously, and RAV and DAV are measured in the Earthcentered, ICRF frame.
4. SIMULATION RESULTS
As discussed previously, the TIP to make a trajectory toward to the L1 or L2 point is directly related to the ecliptic plane crossings and the direction of the Anti-Sun vector for the L1 point transfer and the Sun vector for the L2 transfer, respectively. Also, the location of the launch site, the Naro space center for this study, is again closely related to the TIP. Considering the latitude of the the NARO Space Center as well as its limits on launch azimuth angle, the preferred launch period for the L1 or L2 transfer from NARO Space Center would be near summer solstice for the L1 point mission or winter solstice for the L2 point mission, respectively. Near summer solstice the declination of the anti-Sun vector is about –23.4 deg and about 23.4 deg for the Sun vector. These declinations are the extrema values that the Sun direction could have for the Earth equatorial plane, indicating that the spacecraft launched from NARO Space Center could have the opportunity to have a shorter coasting time before reaching the TIP. Otherwise, the spacecraft launched from NARO Space Center may have a longer coasting time for short coast cases to meet TIP conditions, i.e., one more orbit of the Earth for ecliptic plane crossing conditions. A more in-depth discussion will be made in the following subsection regarding the launch geometries from NARO Space Center.
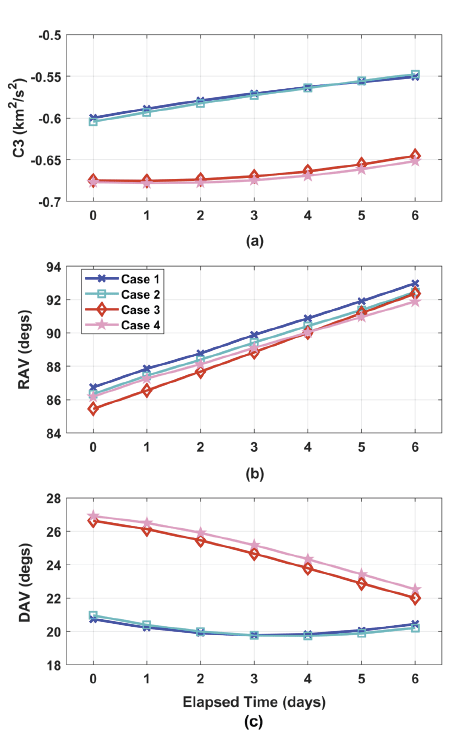
For these reasons, the current work narrowed down the candidate launch periods for the L1 and L2 point missions from NARO Space Center. For L1 point transfer, seven days of potential launch period is selected from 18 Jul 2030 to 24 Jul 2030, and also seven days from 18 Dec 2030 to 24 Dec 2030 for L2 point transfer case, which are all near summer and winter solstices. Here, readers may note that other dates not selected in this work are not indicating “cannot be launched” dates, and still can be used as launch dates but will have more coasting time. On every single launch date, there exist two launch opportunities to meet the TIP for TLI burn, and these two launch cases will form “short” and “long” coast cases before reaching the TIP. In the following discussion, “Case 1” will refer short coast case for the L1 transfer, “Case 2” is for the long coast case of the L1 transfer, and “Case 3 and 4” are for short and long coast cases of the L2 point transfers, respectively.
Fig. 2 shows the TIP parameter variations of four simulation cases for different launch days. In Fig. 2(a) C3 magnitude is shown and RAV and DAV are shown in Fig. 2(b) and (c), respectively. In Fig. 2, the x-axis indicates elapsed days since 18 Jun 2030 for Cases 1 and 2, and elapsed days since 18 Dec 2030 for Cases 3 and 4. As shown in the Fig. 2(a), required C3 magnitude of Cases 3 and 4, L2 transfers, is slightly less than (–0.678 to –0.645 km2/s2) to those of values (–0.604 to –0.548 km2/s2) for Cases 1 and 2, L1 transfers. If these C3 magnitudes are converted into TLI delta-V burn magnitude with regarding 300 km of altitude, then, the ranges of TLI delta-V burn magnitude are found to lie in 3,172.454–3,176.072 m/s for Cases 1 and 2, and 3,168.907– 3,170.938 m/s for Cases 3 and 4. Even iprk is assumed to have 80 deg, the TLI burn magnitudes are slightly more (about several m/s more) than those of the values required with lesser parking orbit inclination, i.e., 23.5 deg, which was found to be about 3,165.094 m/s with the same targeting conditions. For RAV, shown in Fig. 2(b), it increases (from 85.453 to 92.971 degs) with day elapsed, regardless of different simulation cases (towards L1 or L2) which is quite nominal behavior. For DAV characteristics, shown in Fig. 2(c), Cases 3 and 4 tends to have slightly more DAV than Cases 1 and 2, and these behaviors are strongly dependent on the relation between the equatorial and ecliptic plane at the moment of instantaneous TLI burn.
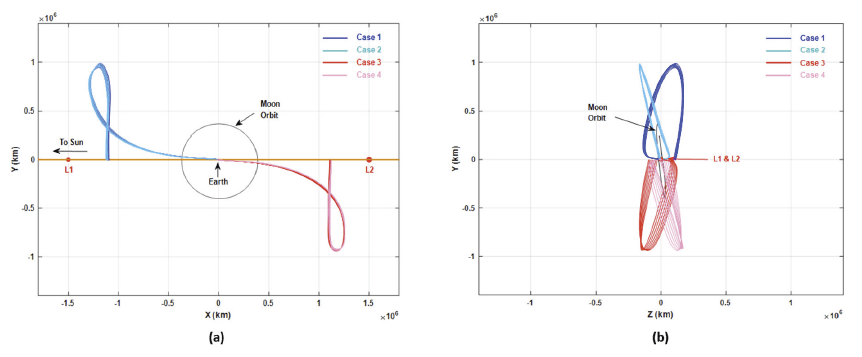
In Fig. 3(a) and (b), the shape of transfer trajectories for all four different cases are depicted. Fig. 3 (a) shows transfer trajectories projected onto XY plane of the Earth-centered, SER frame and shown in Fig. 3(a) is the projection onto the ZY plane of the Earth-centered, SER frame. As shown in Fig. 3(a), every resultant transfer case crossed the ZX plane, as given as a targeting constraint, namely the constrained Y-axis component to be zero, near at L1 or L2 points. Even though the shape of the transfer trajectories shown in Fig. 3(a) looks very similar, shapes seen from the side [ZY plane projection view shown in Fig. 3(b)], are completely different. Due to the launch geometry from the NARO Space Center, especially the initial parking orbit’s inclination, the resultant trans-Lagrange point trajectory does not follow the ecliptic plane, resulting in slightly inclined trajectories concerning the ecliptic plane. Transfer time to reach the ZX crossing point was found to be about 100 days after TLI burn regardless of L1 or L2 point transfer. At the ZX crossing point, the LOI burn is usually performed to circularize the spacecraft around the Lagrange points. Further details on LOI burns as well as OM burns will be discussed in the following subsection.
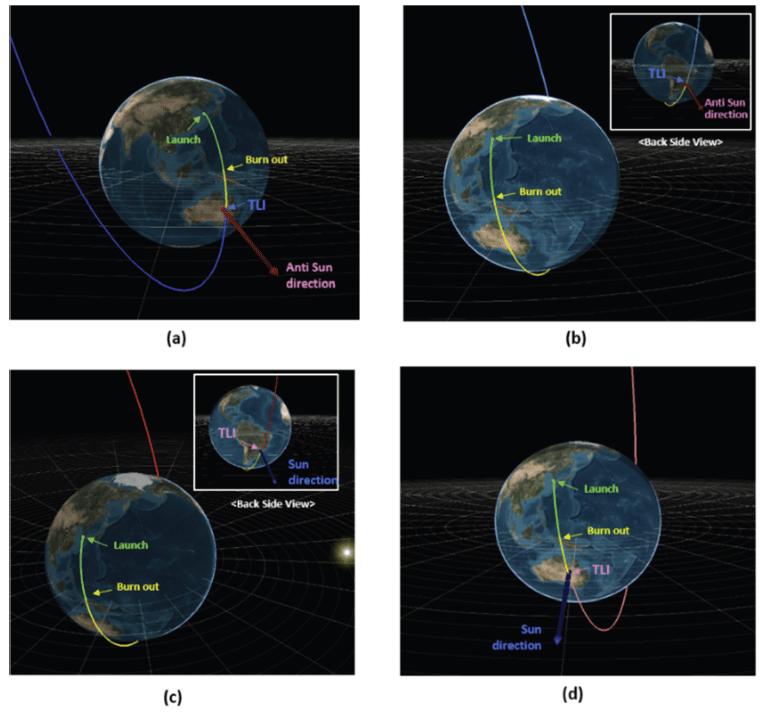
As already discussed, there exist two launch opportunities per day to meet the TIP for TLI burn. More in-depth analyses of daily launch opportunities will be made in the current subsection. Due to the nature of L1 and L2 geometry, the TIP location for the L1 transfer will be at the night side (about the anti-Sun direction vector) and dayside (about the Sun direction vector) for the L2 transfer. This geometry restricts the daily launch time from any specific launch site, together with the required burnout time for the specified launch vehicle and available coasting time. Among seven days of launch opportunities simulated, four representative cases are selected and the launch geometries are shown in Fig. 4. At the top of Fig. 4, launch geometry for the L1 transfer is shown. Fig. 4(a) corresponds to Case 1 and Fig. 4(b) for Case 2 which are the short and long coast cases, respectively. To plot Fig. 4(a) and (b) the launch date of Jun 18 2030 is selected. For Case 1, the launch time is found to be at about 14:42:56 (UTC) resulting in TIP for TLI burn time to be about 15:02:42 (UTC) which is about 20 min after launch time. Therefore, the spacecraft should be launched almost at midnight in Korea Standard Time (KST) and a coasting time of less than 20 min is required (regarding launch vehicle burn out duration) to achieve the TIP. The geometry of the launch trajectory, coasting orbit, and TIP for TLI burn can be seen in Fig. 4(a) for this case. Here, readers may note that if the launch date is not near the summer solstice, indicating the angle between the zenith vector of NARO Space Center and the anti-Sun vector is less than the current, then, the coasting time would be much shorter or in some cases, the spacecraft should revolve one more orbit around the Earth to achieve TIP for TLI burn for this case. Another example is shown in Fig. 4(b) for Case 2. Unlike Case 1, the launch time for Case 2 is found to be about 03:15:11 (UTC) with TLI burn time of 04:09:33 (UTC). This is the “dayside” launch case concerning the location of NARO Space Center having a coasting duration of about 44 min. The separated spacecraft will execute TLI burn after a half orbit around the Earth to achieve TIP, resulting in the long coasting solution, as shown in the “backside view” of Fig. 4(b). Similarly, launch geometry for Case 3 and 4 are depicted in Figs. 4(c) and (d). Fig. 4(c) corresponds to night side launch with long coast case launched on Dec. 18. 2030 15:13:01 (UTC) with TLI burn time of Dec 18, 2030, 16:05:56 (UTC), resulting in about 42 min of coasting duration. The dayside launch with short coast case toward the L2 point is shown in Fig. 4(d). For this case, launch time is found to be at about Dec 18, 2030, 02:35:58 (UTC) with TLI burn time of Dec 18, 2030, 02:57:20 (UTC) having about 22 min of coasting duration. Based on the current results, it is expected that further progress on daily launch time can be made after the establishment of detailed mission concepts, especially, with the solid launch vehicle performances. More details on design parameters discussed in the subsection of 4.1.1 can be found in Appendix (Table A1-A4).

|

|

|

|
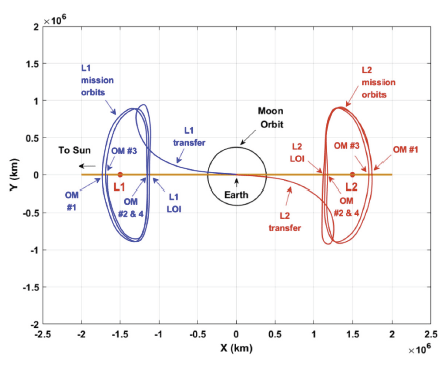
After about a 100 day transfer, the spacecraft will intercept the ZX plane crossing point (shown in Fig. 3) and will perform an LOI maneuver to insert the spacecraft into its intended mission orbit at the vicinity of L1 or L2 and may execute an OM maneuver to maintain the desired orbit. Here, readers may again remember assumptions and limitations that have been made in this work during LOI and OM simulation as discussed in Section 2 under step 3. In Table 1, two representative example results are shown. “Example 1” analyzed the L1 point orbiting case launched on 18 Jul 2030 and “Example 2” is for the L2 point orbiting case launched on 18 Dec 2020. Both examples are short coast cases with night side launch for “Example 1” and a dayside launch case for “Example 2”. In Table 1, detailed burn time and relevant delta-V magnitude for both LOI and OM maneuvers are shown. As seen from Table 1, the LOI showed the largest burn among LOI and OM burns, and the overall delta-V magnitude for “Example 1” is about 58.177 m/s and about 66.640 m/s for “Example 2” to perform more than a one year mission. The OM maneuvers were found to be executed periodically for approximately 3 months which is about half of the period of an orbit around the Lagrange points. This is since all OM maneuvers are planned to be executed at every intercept moment of ZX plane crossing points. Once again, readers may note here that results provide in this subsection are only an example, and may strongly differ for each difference in mission orbit targeting parameters. The LOI burn magnitude for DSCOVR mission was about 167 m/s (Roberts et al. 2015), about 33.8 m/s for SOHO, and about 15.4 m/s for NGST mission (Guzman et al. 1998), respectively. For ranges of OM burn magnitudes, details on each past mission executed burns will not be addressed here as their ranges are so wide as well as dependent on each mission's objectives. In Fig. 5, an example of mission orbits with transfer trajectories around the L1 and L2 points is shown in XY plane projection of the Earth-centered, SER frame.

|
5. CONCLUSIONS
The current work analyzed the early feasibilities of the Sun-Earth Lagrange point missions launched from NARO Space Center. L1 and L2 points are selected as candidate Lagrange points which are suitable for solar and astrophysics missions. The L1 and L2 point targeting problem is formulated with high fidelity dynamics models and relevant mission parameters are analyzed including preferable launch period, TIP conditions, and characteristics of the daily launch window from NARO Space Center. Also, TLI, LOI, and OM maneuver characteristics are analyzed. Unlike LEO or GEO missions which have launch restrictions due to NARO Space Center’s geolocation and launch azimuth, TLC trajectory toward L1 or L2 could be achievable from NARO Space Center. To inject the spacecraft toward the L1 or L2 points, it is discovered that a launch near summer or winter solstices would be the better choice to secure shorter coasting arc durations before TLI burn. There exist two launch opportunities per day to inject the spacecraft toward L1 or L2 points from NARO Space Center. One with the short coast arc that has about 20 min of coasting and the long coast arc case with about 45 min of coasting time. The ranges of required C3 magnitudes for the analyzed launch periods seem to quite acceptable to be launched from NARO Space Center, –0.604 to –0.548 km2/ s2 for L1 transfer and –0.678 to –0.645 km2/s2 for L2 transfer, respectively. For the aspect of LOI and OM burns, even many assumptions are made to simplify the problem, the magnitude of LOI and OM burns are much less than the typical lunar missions orbiting the Moon at about 100 km altitude. This indicates that the missions in the vicinity of L1 or L2 could be conducted with much smaller spacecraft, and therefore, such a mission could be another option for future Korea’s deep-space missions. Even the current work is conducted under many assumptions that are needed to be resolved and to be matured, results from the current work could be a good starting point to extend the diversity of future Korean deep-space missions.