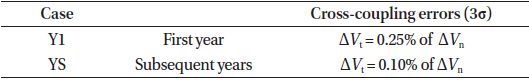Geostationary Satellite Station Keeping Robustness to Loss of Ground Control

The orbit propagator is based around the set of modified equinoctial orbital elements defined in Walker et al. (1985). Orbit propagation is a hybrid of analytical propagation and numerical propagation with a time step of 10 minutes (600 seconds). The orbit propagator models perturbing forces generated by:

Station keeping maneuvers are modeled as ‘impulsive maneuvers’. That is, each station keeping maneuver is modeled as a momentaneous velocity change (ΔV) at the time mid-way between the start and end of the maneuver. This is a common and adequate approximation for maneuvers with short durations compared to the orbital period and/or with durations shorter than the integration step, which is typically true for station keeping maneuvers using chemical propulsion as well as many station keeping maneuvers using electrical propulsion. Longer duration maneuvers are better modeled as ‘finite maneuvers’ (nonimpulsive maneuvers) but are beyond the scope of this study.

The ΔV of each maneuver is separated into components normal (ΔV_n), radial (ΔV_r) and approximately tangential (ΔV_t) to the orbit. More precisely:

The orbit propagator applies these ΔV components to the modified equinoctial orbit elements as prescribed in Walker et al. (1985). We do not attempt to model maneuver minimum impulse bit limitations or expected (predictable) maneuver cross-coupling. Instead we assume that the nominal theoretical maneuver ΔV is achievable and indeed the expected value for any maneuver.

For East-West (EW) maneuvers we assume a 3σ maneuver performance uncertainty of 1% and disregard cross-coupling errors as negligible. We furthermore assume that all EW maneuvers are planned for a single-burn sun-pointing eccentricity control strategy only. For North-South (NS) maneuvers assume a 3σ tangential cross-coupling error of either 0.1% or 0.25% as explained in section 3.5. Radial cross-coupling error is disregarded as being of secondary importance compared to tangential cross-coupling. Furthermore, we assume that all NS maneuvers in a given calendar year are planned with the same magnitude and centered on a spacecraft right ascension of 90° for South maneuvers or 270° for North maneuvers, which, for the purposes of our analysis, we consider to be a sufficient approximation of the minimum fuel inclination control strategies typically employed for geostationary satellites.

A satellite’s latitude has a cyclical variation throughout the day with the peak positive (north) and negative (south) latitudes being equal to the inclination (i) of the satellite’s orbit. To keep the satellite latitude within a ± 0.05° window, for example, one must maintain the orbit’s inclination below i_max = 0.05° . In terms of equinoctial parameters the inclination equals the length of the inclination vector, that is, $i=\sqrt{i_{\text{x}}^2+i_{\text{y}}^2}$. Thus the maximum allowed inclination can be represented in the plane of the inclination vector as a circle of radius i_max centered on origo. By biasing the inclination vector to the appropriate edge of the circle the inclination free drift duration can be maximized. By targeting inclination control maneuvers to allow a nearmaximum inclination vector free drift time about five weeks of inclination vector free drift can be achieved within a ± 0.05° latitude window during worst case years, increasing to almost 7 weeks during best case years (refer to section 3.8 for a further discussion of this time-varying aspect). With a ± 0.1° latitude window the free drift duration doubles.

Given the relatively long free drift duration with i ≤ i_max for common latitude windows and the fact that it has only minor sensitivity to maneuvers performance errors the latitude is rarely the critical or limiting factor in terms of violating orbit geometry requirement; the longitude window tends to be violated well in advance of the latitude window. Furthermore, maintaining strict latitude control is generally of lower importance than maintaining strict longitude control since latitude window excursions neither increase the risk of radio frequency interference nor the risk of physical collisions with neighboring geostationary satellites (on the contrary, large latitudes generally increase both angular and physical separation with other geostationary satellites). For these reasons it is not uncommon to have more lax requirements for a satellite’s latitude window than for its longitude window, for example ± 0.1° in latitude versus ± 0.05° in longitude.

In some literature the inclination vector is defined as the two-dimensional projection of the normal vector of the orbital plane onto the equatorial plane. However, in flight dynamics software suites in use by satellite operators the predominant definition of the inclination vector has it pointing towards the ascending node of the orbit. In order for readers to benefit from their experience with operational flight dynamics software suites we have chosen to use the latter definition in the figures in this paper.

Inclined geosynchronous orbits are beyond the scope of this study, but in general do not impact the conclusions. A large orbital inclination will cause a daily libration in longitude on the order of 0.0044°, 0.017°, and 0.039° for inclinations of 1°, 2°, and 3°, respectively (Soop 1994). However, the extremes of these librations are reached at half the maximum/minimum latitudes while they are practically zero near the geostationary (equatorial) plane. Any neighboring satellites in inclined orbits will experience similar and synchronized librations ensuring that longitude separation is maintained at high latitude.

Due to the relatively large cross-coupling of NS maneuver ΔV into the orbital plane it is generally desirable to perform an EW maneuver as soon as possible after an NS maneuver in order to compensate for any unpredicted in-plane ΔV component. Failure to do so can allow the satellite’s longitude to diverge rapidly from the desired/predicted longitude. The limiting factor on how soon after the NS maneuver the EW maneuver can be performed is the collection of measurement data for orbit determination, performing the orbit determination itself in order to assess the NS maneuver performance (including any crosscoupling), and the planning and uploading of an EW maneuver that will compensate for both the NS maneuver cross-coupling and the longitudinal acceleration the satellite will be subjected to until the next EW maneuver. The most time consuming of the above steps is the collection of measurement data for the orbit determination; typically at least 24 hours of data is desired. Taking all steps into account it is generally possible to execute the EW maneuver on the second or third day following the NS maneuver.

Given the above context we can identify the worst possible time for the satellite operator to lose ground control capability: after execution of the NS maneuver but before the following EW maneuver has been uploaded to the satellite. In this situation the longitude control has been impacted by the cross-coupling of the NS maneuver but the loss of ground control prevents the satellite operator from compensating for the cross-coupling with an appropriately planned EW maneuver. To represent this worst case timing for the loss of ground control in our study we simulate a loss of ground control starting on the day following a NS maneuver. The day of loss of ground control is considered ‘day zero’ in the simulations.

Initial orbital parameters for the simulations have been chosen to provide a longitude evolution well centered in the station keeping window assuming that nominal station keeping operations can proceed indefinitely (i.e., without loss of ground control capability) and a maximized inclination free drift duration within a ± 0.05° latitude window.

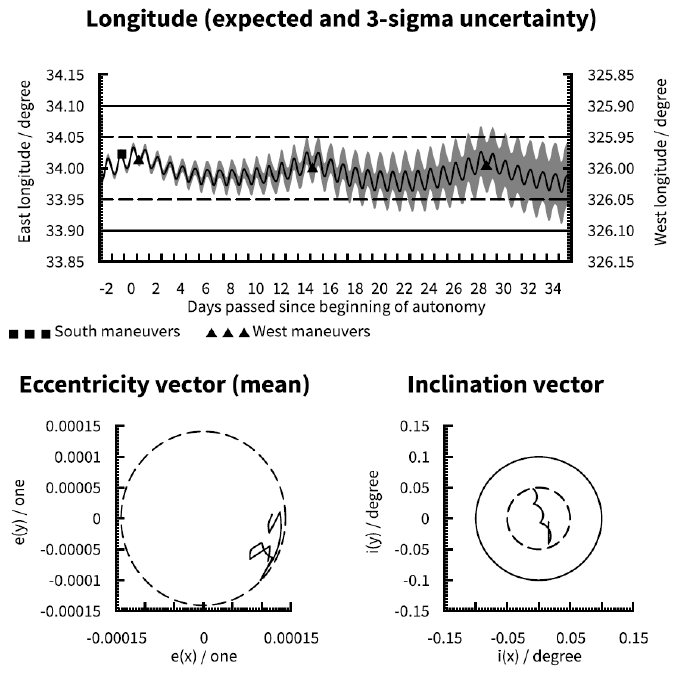
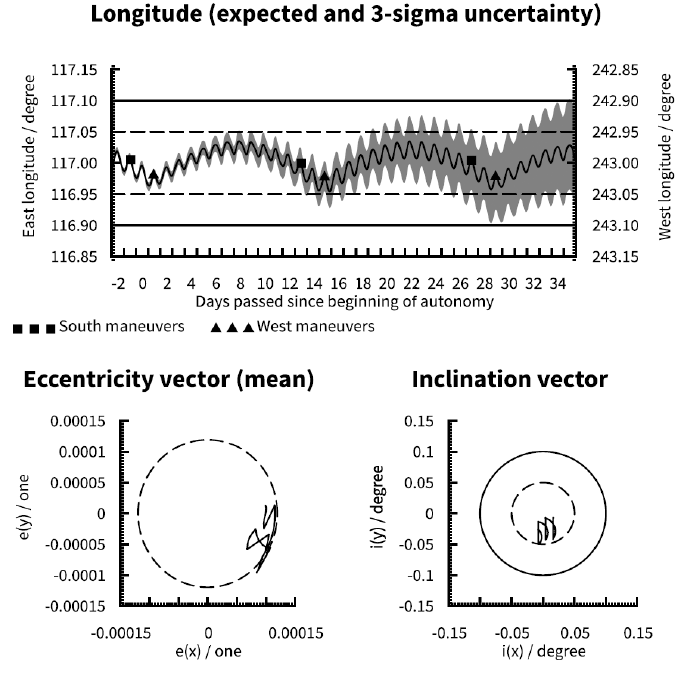
Fig. 1 represents the baseline case that we have chosen for this parametric study: a hypothetical satellite being operated at 117° E with a 14 day station keeping maneuver cycle. An assumed effective cross-section to mass ratio of 0.03 m²/kg allows the satellite to be comfortably operated at this longitude with a propellant-optimal single-burn sunpointing eccentricity control strategy. Orbit determination is performed with a single ground station providing tracking and ranging data. It is assumed that multiple EW maneuvers but no NS maneuvers are pre-loaded for execution in case of loss of ground control capability. The year 2024 is chosen for the baseline case simulation. It is also assumed that the satellite has been operated at least one full year in orbit prior to the starting point of the simulation. The baseline case bears designation 117E_O1_YS_1414_D_2024.

Fig. 1. Case 117E_O1_YS_1414_D_2024 (ΔV_NS = –1.959 m/s, ΔV_EW = –0.079 m/s). Upper half: Expected evolution of the satellite longitude (black line) and 3σ uncertainty of the longitude evolution (gray area). Lower left: Evolution of the satellite orbit’s eccentricity vector (mean values). Lower right: Evolution of the satellite orbit’s inclination vector. This is the baseline case at 117° E [117E], with single station orbit determination [O1], more than a year in orbit [YS], 14 day NS and EW maneuver cycles [1414] and pre-loaded EW maneuvers [D] in the year 2024 [2024]. NS, North-South; EW, East-West.

Download Original Figure

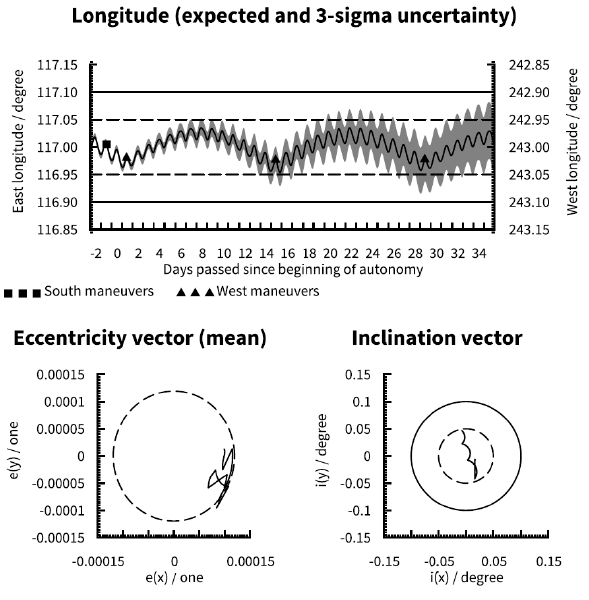
In the upper half of Fig. 1 the longitude evolution of the satellite is shown. The black line within the grey area shows the expected evolution of satellite longitude (y-axis) over time (x-axis) while the grey area shows the 3σ uncertainty of the longitude evolution. Day 0 of the x-axis is the day on which ground control capability is assumed to be lost. The dashed and solid lines show two typical station keeping window boundaries. The square and triangular markers on the black line show the times and expected longitudes at which NS and EW maneuvers, respectively, are performed. The lower left quarter of Fig. 1 shows the evolution of the satellite orbit’s eccentricity vector. For clarity daily mean values of the eccentricity vector are shown, with diurnal librations suppressed. The dashed circle represents the target mean eccentricity for the single-burn sun-pointing eccentricity control strategy. The eccentricity vector is expected to roughly track the circle as it rotates in a counterclockwise fashion about origo throughout a year. The lower right quarter of Fig. 1 shows the evolution of the satellite orbit’s inclination vector. The dashed and solid circles correspond to typical latitude window boundaries of ± 0.05° and ± 0.1° respectively.

For the baseline case we can see that there is a small possibility that a longitude window of ± 0.05° would be marginally and briefly violated as soon as 8 days after a loss of ground control. There is a much larger likelihood of violation of a ± 0.05° longitude window after 14 days, at which time violations may be quite large and in excess of half a day. On the other hand there is no risk within 3σ that a longitude window of ± 0.1° would be violated within the simulation period stretching until 35 days after a loss of ground control. Finally we can see that with an appropriately biased initial inclination vector the orbital inclination will remain below 0.05° (satellite latitude will remain within ± 0.05°) during the simulation period.

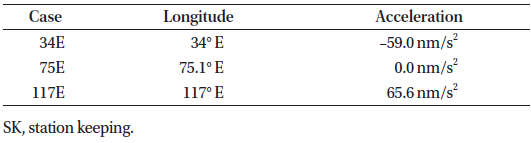
The size of the station keeping window obviously directly impacts the duration that the window can be maintained without ground intervention. We investigate the impact of two commonly used longitude station keeping window sizes (Table 1). In all figures the limits for both cases are shown, ± 0.05° with dashed lines and ± 0.10° with solid lines.

Table 1. Cases of longitude station keeping (SK) window size

Download Excel Table

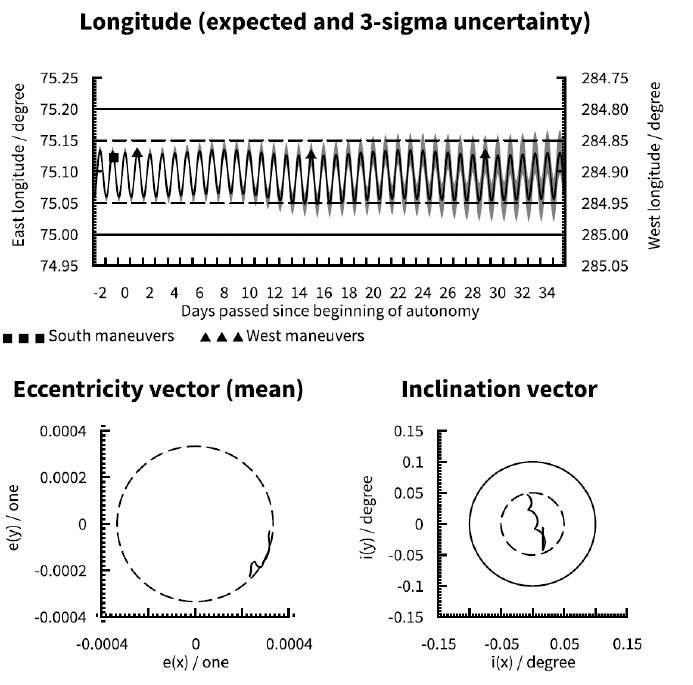
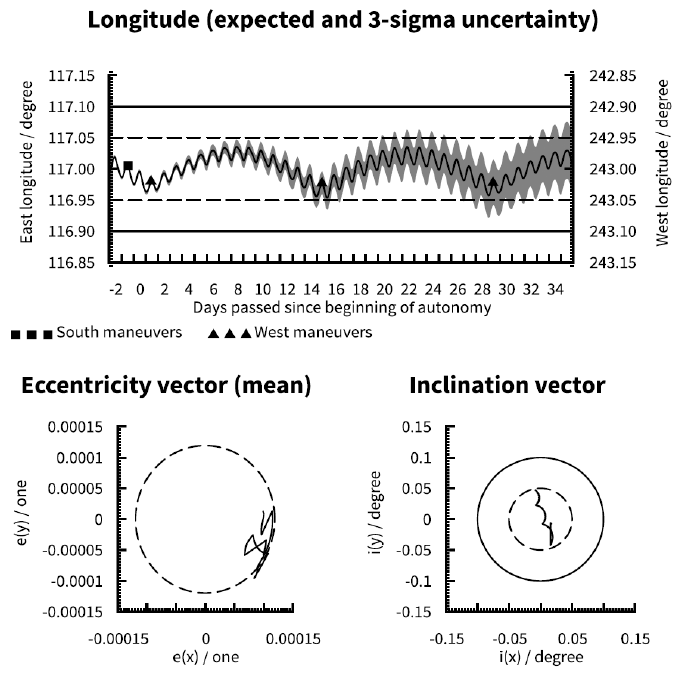
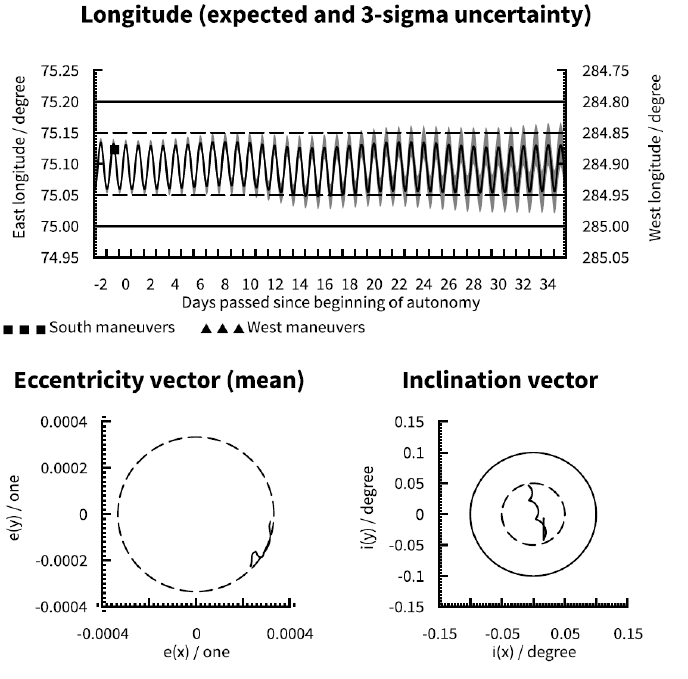
Due to the fact that Earth’s gravity field is not perfectly spherically symmetric the longitudinal acceleration (that is, the rate of change of a satellite’s drift rate) varies with longitude. The longitudinal acceleration is zero at four longitudes (–105.3° E, –11.5° E, 75.1° E, and 161.9° E) while maximum acceleration is near 117° E and maximum deceleration is near 34° E (Soop 1994). To illustrate the impact of longitudinal acceleration three different station keeping longitudes as shown in Table 2 have been investigated. Note that with a single-burn sunpointing eccentricity control strategy the orbit eccentricity is maximum for a zero longitudinal acceleration and decreasing with increasing absolute value of the acceleration.

Table 2. Cases of SK longitude

Download Excel Table

Compare Fig. 1 (117° E), Fig. 2 (34° E) and Fig. 3 (75.1° E). The lower absolute longitude acceleration at 34° E compared to 117° E allows a slightly tighter longitude control at 34° E. At 75.1° E the mean longitude is effectively constant but, due to the EW maneuver ΔV for longitude control being zero, the eccentricity is effectively uncontrolled and thus much larger than in the other two cases.

Fig. 2. Case 34E_O1_YS_1414_D_2024 (ΔV_NS = –1.959 m/s, ΔV_EW = 0.071 m/s). As the baseline case (Fig. 1) but at 34° E longitude [34E].

Download Original Figure

Fig. 3. Case 75E_O1_YS_1414_D_2024 (ΔV_NS = –1.959 m/s, ΔV_EW = 0.000 m/s). As the baseline case (Fig. 1) but at 75.1° E longitude [75E].

Download Original Figure

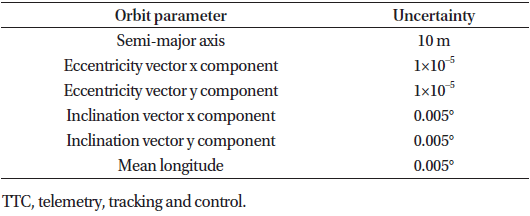
In our baseline case we assume the following 3σ uncertainties in the orbit knowledge at the start of the simulation periods. We consider these uncertainties to be representative bounds of orbit determination accuracy for geostationary satellites using range, azimuth and elevation measurement data from a single TTC antenna (Table 3). The actual uncertainties will be functions of the performance and calibration of TTC antenna and satellite hardware as well as the geographical location of the TTC antenna with respect to the satellite.

Table 3. Orbit determination accuracy (one TTC antenna)

Download Excel Table

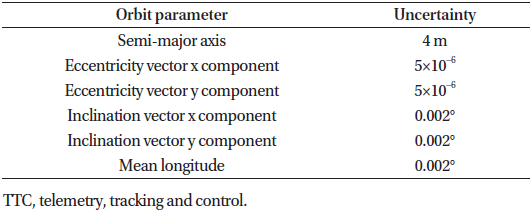
A common method of improving the orbit determination accuracy is by adding range measurements from a second, geographically separated, antenna to the data set used for the orbit determination. A greater geographical separation between the two TTC antennas provides a greater improvement, but in practice logistical and political considerations tend to constrain the choices of TTC antenna locations. We select the following 3σ uncertainties as a representative example of orbit knowledge for orbit determination performed with range data from two TTC antennas geographically separated by 30° in longitude (Table 4).

Table 4. Orbit determination accuracy (two TTC antennas)

Download Excel Table

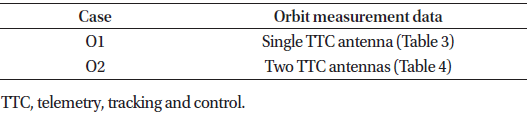
In order to evaluate the impact of using measurement data from a second, geographically separated, TTC antenna for orbit determination we define the following test cases in Table 5.

Table 5. Cases of TTC antenna

Download Excel Table

In Fig. 4 one can see that two TTC antennas provide a slight improvement in longitude station keeping uncertainty with respect to a single antenna (Fig. 1). The difference in longitude uncertainty is quite substantial early in the simulation period, but the additional uncertainties introduced by maneuvers quickly grow to dominate the evolution. Thus we conclude that while orbit determination with two TTC antennas is beneficial under normal operating circumstances the impact on the duration of station keeping window compliance in the absence of ground control capability is quite marginal.

Fig. 4. Case 117E_O2_YS_1414_D_2024 (ΔV_NS = –1.959 m/s, ΔV_EW = –0.079 m/s). As the baseline case (Fig. 1) but using two TTC antennas for orbit determination [O2]. TTC, telemetry, tracking and control.

Download Original Figure

Any station keeping maneuvers will inevitably, due to thruster alignments and plume impingements, have ΔV components in directions other than the nominal (tangential to the orbit for EW maneuvers, normal to orbital plane for NS maneuvers). When such off-nominal ΔV components are predictable and of limited magnitude they do not significantly impact the ability to maintain a satellite within its station keeping window. Off-nominal ΔV component are often referred to as maneuver triaxiality or cross-coupling, and any unpredictability in these components as crosscoupling errors. The cross-coupled ΔV component can often be on the order of 1% of the nominal ΔV component, with the cross-coupling errors on the order of 0.1% of the nominal ΔV component.

EW station keeping maneuvers are relatively small (on the order of 0.01 m/s per week) and it follows that any off-nominal ΔV components will also be small. For some satellite designs the EW maneuvers may have significant but predictable radial ΔV cross-coupling, but the crosscoupling errors of EW station keeping maneuvers can be considered negligible. The ΔV of NS station keeping maneuvers performed with chemical propulsion are on the order of 1 m/s per week so even a relatively small tangential cross-coupling component can be significant in comparison to EW station keeping maneuvers. More importantly, the cross-coupling errors can significantly impact the ability to maintain a satellite within its longitude station keeping window. In order to minimize the impact of NS station keeping maneuvers on longitude station keeping it is common practice to take into account predicted crosscoupling from upcoming NS station keeping maneuvers when planning an EW maneuver.

An important contributor to NS maneuver cross-coupling is impingement of the thruster plumes on the solar array of the satellite, which deflects some of the thruster exhaust, and thereby thrust, in an unintended direction (see, e.g., Gibbs et al. 2008). The magnitude and direction of the deflected thrust depends on the orientation of the solar array with respect to the thrusters at the time of firing. The local satellite time at which fuel-optimal NS maneuvers are performed varies throughout the year, and thus the solar array angle with respect to the satellite body (and thrusters) at the time of NS maneuvers also varies throughout the year. In order to accurately predict the NS maneuver crosscoupling (and minimize the cross-coupling errors) the impact of the varying solar array angle must be accounted for. For the first year of operating a satellite the crosscoupling as a function of solar array angle is typically predicted on the basis of the satellite manufacturer’s mathematical models of the satellite geometry and thruster plume behavior. However, after a satellite has been operated for a full year the satellite operator will have collected NS maneuver performance data, including observed crosscoupling, for a large amount of evenly distributed solar array angles. By calibrating the NS maneuver cross-coupling predictions on the basis of the observed cross-coupling in orbit, the accuracy of the cross-coupling predictions can typically be significantly improved and the cross-coupling errors minimized for future NS maneuvers. To illustrate the impact of the NS maneuver cross-coupling errors we model both the first year in orbit with a typical 3σ tangential crosscoupling error as well as subsequent years with improved cross-coupling prediction and reduced cross-coupling errors, as shown in Table 6.

Table 6. Cases of cross-coupling error

Download Excel Table

When comparing Fig. 1 and Fig. 5 one can see the significant improvement in longitude station keeping uncertainty afforded by more accurate cross-coupling predictions. This implies that it is well worth the effort for a satellite operator to, after the first year in orbit, update the cross-coupling data (which is often in the form of lookup Tables or polynomial coefficients) used by its flight dynamics software to predict the cross-coupling of future NS maneuvers.

Fig. 5. Case 117E_O1_Y1_1414_D_2024 (ΔV_NS = –1.959 m/s, ΔV_EW = –0.079 m/s). As the baseline case (Fig. 1) but during the first year in orbit [Y1].

Download Original Figure

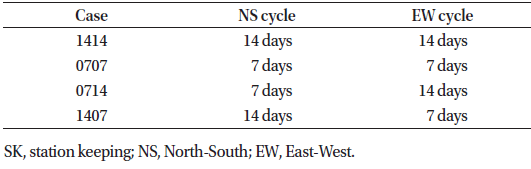
The most commonly used station keeping cycle durations for geostationary satellites are of either 14 days or 7 days. The obvious benefit of choosing a station keeping cycle duration that is a multiple of seven is that it allows a regularity aligning the cyclic activities to be performed in the satellite control center with the weekly work schedule of the control center staff. To minimize operational effort a 14 day station keeping cycle is typically preferred if it can be accommodated by the station keeping window longitude and size, orbit determination accuracy, and satellite characteristics and operational constraints. When this is not the case a 7 day station keeping cycle must be chosen instead, effectively doubling the operational effort. Only in rare cases or with large station keeping windows are station keeping cycles of 21 days or more feasible. Trying to maximize the station keeping cycle to, for example, 18 days in order to minimize operational effort is generally not worth the trade-off against the added personnel, planning and logistical complications arising from the station keeping activities not being aligned with weekly work cycles. For the purposes of this paper we have limited our simulations to 7 day and 14 day cycles. Note that EW and NS cycles do not necessarily have to have the same durations and we have simulated different combinations of EW and NS cycles (Table 7).

Table 7. Cases of SK cycle duration

Download Excel Table

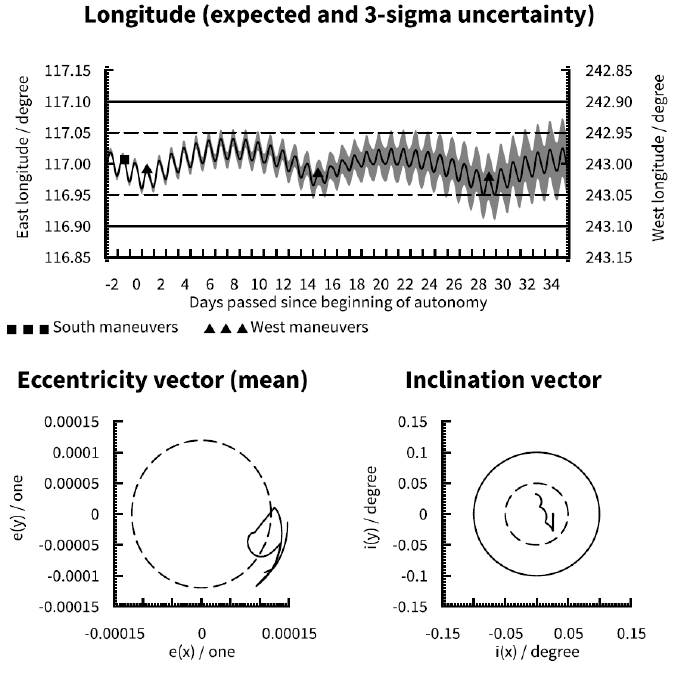
When comparing Fig. 1 (14 day NS and EW cycles), Fig. 6 (7 day NS and EW cycles), Fig. 7 (7 day NS cycle and 14 day EW cycle) and Fig. 8 (14 day NS cycle and 7 day EW cycle) it is clear that reducing the station keeping cycle durations allows for tighter longitude control. It is easy to understand that a shorter EW cycle allows tighter control of the longitude around the center of the station keeping window, even if the longitude uncertainty itself is not substantially impacted. However, it is worth noting that station keeping robustness is improved even when only the NS cycle duration is reduced (Fig. 7). This is due to the cross-coupling from the NS maneuver at the start of the simulation being halved with respect to the baseline case (Fig. 1), with a corresponding reduction in longitude uncertainty. This effect is also clearly seen when comparing Figs. 6 and 8.

Fig. 6. Case 117E_O1_YS_0707_D_2024 (ΔV_NS = –0.979 m/s, ΔV_EW = –0.040 m/s). As the baseline case (Fig. 1) but with 7 day NS and EW maneuver cycles [0707]. NS, North-South; EW, East-West.

Download Original Figure

Fig. 7. Case 117E_O1_YS_0714_D_2024 (ΔV_NS = –0.979 m/s, ΔV_EW = –0.079 m/s). As the baseline case (Fig. 1) but with 7 day NS maneuver cycles [0714]. NS, North-South.

Download Original Figure

Fig. 8. Case 117E_O1_YS_1407_D_2024 (ΔV_NS = –1.959 m/s, ΔV_EW = –0.040 m/s). As the baseline case (Fig. 1) but with 7 day EW maneuver cycles [1407]. EW, East-West.

Download Original Figure

On modern satellites the command parameters for one or several station keeping maneuvers can be pre-loaded in advance of the maneuver execution time as so-called ‘time tagged commands’. The commands are ‘tagged’ with the desired execution time, and when the time arrives the satellite executes the commands automatically without ground intervention. Should the need arise any uploaded time tag commands can be deleted by ground command prior to their execution time. Pre-loaded maneuvers can be used to allowed continued station keeping maneuvering in the case of loss of ground control. We look at the impact of several cases of maneuver pre-loading, ranging from no pre-loading to indefinite pre-loading of both NS and EW maneuvers to pre-loading of EW only (Table 8). The cases applicable to a given satellite may depend of the capabilities of the satellite itself. Note that in cases C and D the preloaded EW maneuvers are sized based on the assumption that no additional NS maneuvers (after the one preceding the loss of ground control) will be executed, and thus do not pre-emptively compensate for additional NS maneuver cross-coupling (refer to section 3.5 for a further discussion of maneuver cross-coupling).

Table 8. Cases of pre-loading

Download Excel Table

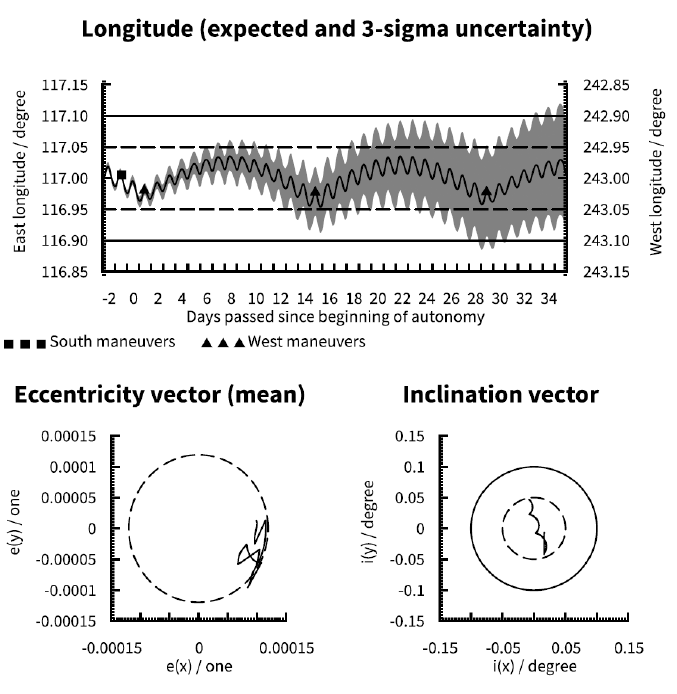
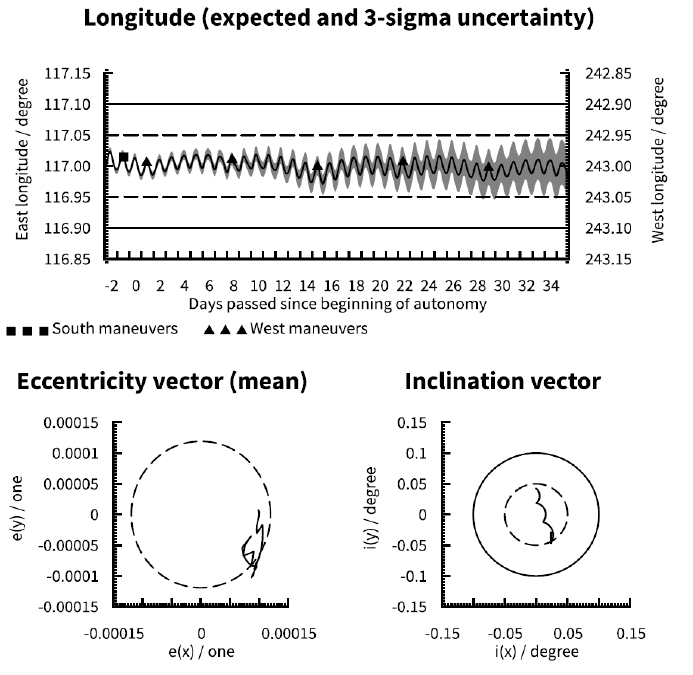
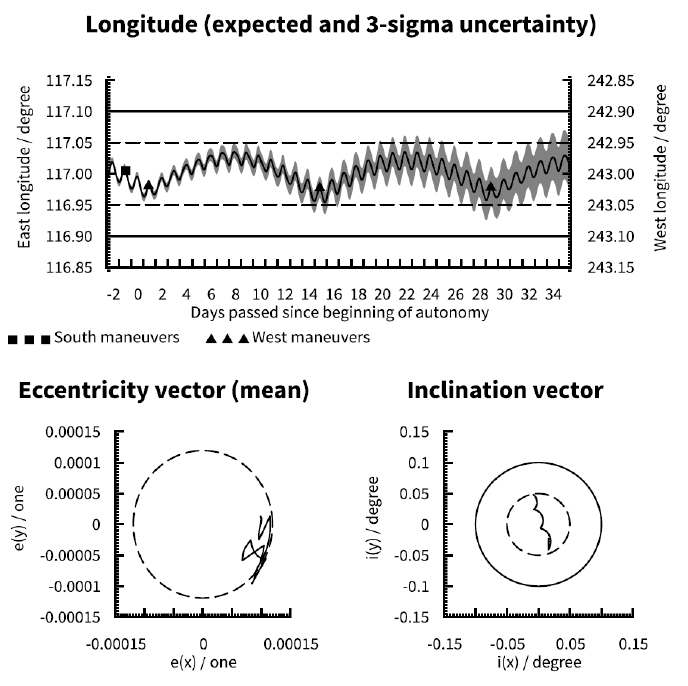
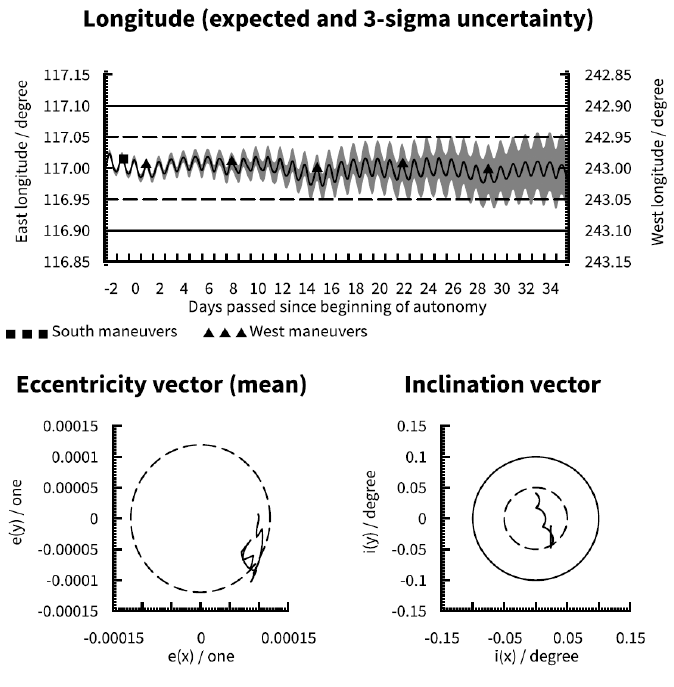
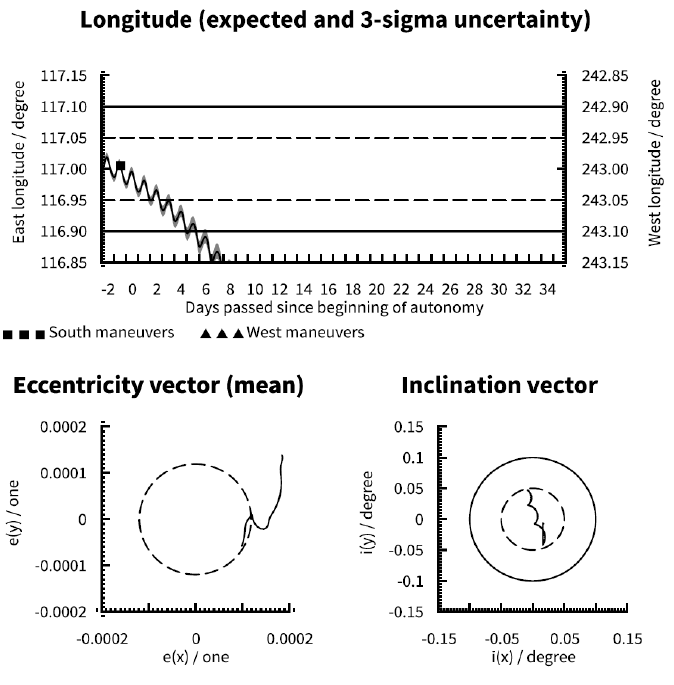
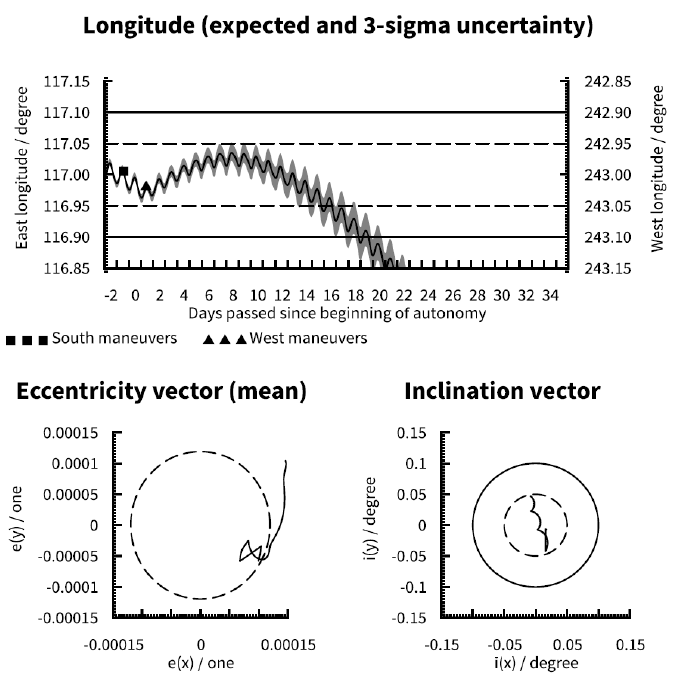
Compare Fig. 1 (indefinite EW maneuvers only), Fig. 9 (no pre-loaded maneuvers), Fig. 10 (indefinite pre-loaded NS and EW maneuvers) and Fig. 11 (indefinite pre-loaded EW maneuvers only). Obviously with no pre-loaded maneuvers (Fig. 9) the satellite will soon exit the longitude window. A single pre-loaded EW maneuver (Fig. 11) can delay the violation of the window-by up to an EW cycle, but this is subject to other parameters affecting the longitude uncertainty. Taking the worst case 3σ uncertainty into account violation of the ± 0.05° longitude window is only delayed by half a cycle with respect to Fig. 9. Pre-loading of indefinite NS and EW maneuvers (Fig. 10) will maintain the expected inclination and longitude evolutions within their respective limits indefinitely, but the accumulated influence of cross-coupling from the NS maneuvers aggravate the longitude uncertainty over time. Given that longitude evolution tends to be the limiting factor for autonomy duration, the optimal scheme is likely to use indefinite pre-loading of EW maneuvers only (Fig. 1) where inclination control is sacrificed for improved longitude control. Note that with ideal initial conditions cases A and D are effectively identical for a satellite at 75.1° E due to the absence of longitudinal acceleration (refer to section 3.3). Compare Fig. 12 (no pre-loaded maneuvers at 75.1° E) to Fig. 3 (indefinite EW maneuvers at 75.1° E).

Fig. 9. Case 117E_O1_YS_1414_A_2024 (ΔV_NS = –1.959 m/s). As the baseline case (Fig. 1) but without pre-loaded maneuvers [A].

Download Original Figure

Fig. 10. Case 117E_O1_YS_1414_B_2024 (ΔV_NS = –1.959 m/s, ΔV_EW = –0.079 m/s). As the baseline case (Fig. 1) but with pre-loaded NS and EW maneuvers [B]. NS, North-South; EW, East-West.

Download Original Figure

Fig. 11. Case 117E_O1_YS_1414_C_2024 (ΔV_NS = –1.959 m/s, ΔV_EW = –0.079 m/s). As the baseline case (Fig. 1) but with a single pre-loaded EW maneuver [C]. EW, East-West.

Download Original Figure

Fig. 12. Case 75E_O1_YS_1414_A_2024 (ΔV_NS = –1.959 m/s). As the baseline case (Fig. 1) but at 75.1° E longitude [75E] and without pre-loaded maneuvers [A].

Download Original Figure

The amount of NS ΔV required for controlling the inclination of a geostationary satellite’s orbit varies with time as the inclination of the moon’s orbit with respect to the equator varies between 18.3° and 28.6° with a period of 18.6 years. The maximum ΔV (51.1 m/s per year) is required when the inclination of the moon’s orbit is at its maximum and the minimum ΔV (40.6 m/s per year) when the inclination of the moon’s orbit is at its minimum (Table 9). During a year with maximum NS ΔV requirement the NS maneuvers will be larger on average and consequently the tangential component of the ΔV (and the uncertainty thereof ) due to cross-coupling will be larger.

Table 9. Cases of SK year

Download Excel Table

Comparing Fig. 1 (2024) and Fig. 13 (2015) it is clearly seen that the inclination is evolving at a slower rate in 2015 than in 2024, which in turn reduces the magnitude of NS maneuvers in 2015. The slightly smaller NS maneuver at the beginning of the simulation period in 2015 leads to a slightly reduced longitude uncertainty with respect to 2024. This can be seen by careful comparison of Figs. 1 and 13 but is somewhat obscured by the orbital eccentricity not being identical in the two cases (due to differences in Earth-Sun- Moon geometry).

Fig. 13. Case 117E_O1_YS_1414_D_2015 (ΔV_NS = –1.556 m/s, ΔV_EW = –0.079 m/s). As the baseline case (Fig. 1) but in 2015 [2015].

Download Original Figure

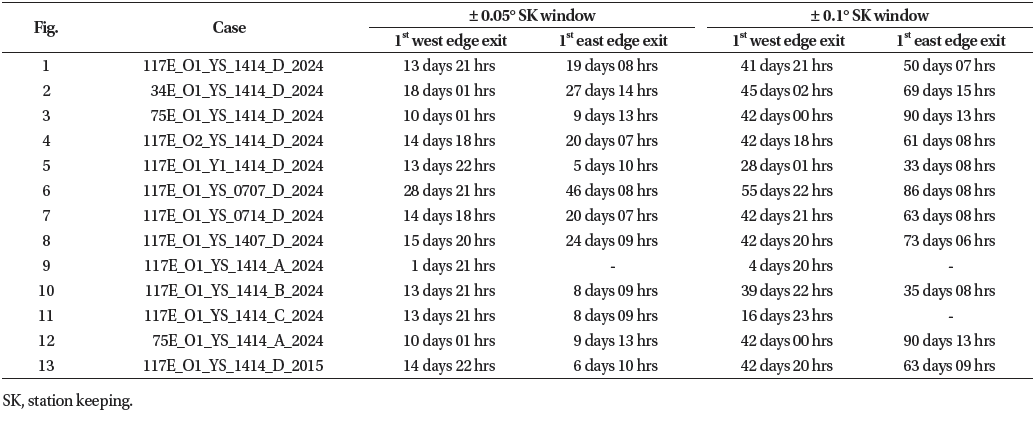
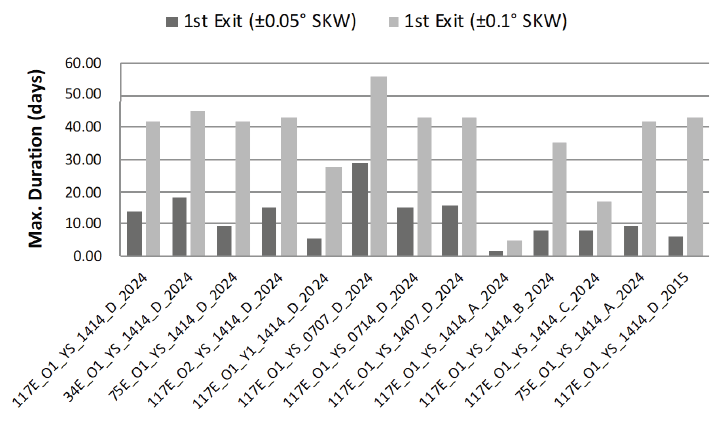
The value of this analysis is primarily qualitative, as any quantitative results will be dependent on a number of factors specific to a given satellite, including satellite effective cross-section to mass ratio, station keeping longitude, orbit determination accuracy, maneuver minimal impulse bit limitations, cross-coupling characteristics and the actual date of loss of ground control capability. Nevertheless, Table 10 provides a quantitative summary of the duration of autonomy before the first longitude station keeping window violation, for ± 0.05° and ± 0.10° station keeping window sizes, for each of the cases presented above. Since the risk of radio frequency interference or physical collisions with neighboring geostationary satellites may not be present on both sides of the station keeping window we present the time of violating the west and east edges of the windows separately. Note that Table 10 shows only the initial times of station keeping window violations without attempting to quantify the magnitude of the violations which are sometimes very slight, such as, e.g., the first + 0.05° east edge violation in Fig. 13 (case 117E_O1_YS_1414_ D_2015). Fig. 14 shows the results in Table 10 graphically, but shows only the first violation for either station keeping window size, without distinguishing between the west and east edges.

Table 10. First SK window east/west edge exit times

Download Excel Table

Consistently with the results of qualitative analysis, it can be observed that the cases B, C and D of station keeping maneuver pre-loading are much more beneficial compared to the case A of no pre-loading, as defined in Table 8. Case D (Fig. 1), with indefinite EW pre-loading only, has 7.4 times longer duration in the ± 0.05° station keeping window while cases B (Fig. 10) and C (Fig. 11) have 4.5 times longer durations compared to case A (Fig. 9) of no pre-loading operation. We observe a bigger impact in the ± 0.1° station keeping window such that case D has 8.7 times longer duration in the station keeping window while cases B and C have 7.3 and 3.5 times longer durations, respectively, compared to case A of no pre-loading operation. These quantitative results of the duration of autonomy confirm that the most beneficial factor for maximizing the time a satellite will remain in the station keeping window is the operational practice of pre-emptively loading East-West station keeping maneuvers for automatic execution on board the satellite should ground control capability be lost. Fig. 14 also shows that the short station keeping maneuver cycle duration, case 0707 (Fig. 6), gives 2.1 and 1.3 times longer duration for the ± 0.05° and ± 0.1° station keeping windows, respectively, compared to case 1414 (Fig. 1) as defined in Table 7. Therefore, we can confirm that reducing the station keeping cycle durations is another secondary beneficial factor for maximizing the duration of station keeping window compliance in the absence of ground control capability.

Fig. 14. Maximum durations within SK windows (± 0.05°, ± 0.1°). SK, station keeping.

Download Original Figure