1. INTRODUCTION
Since 1957, starting with the Soviet Sputnik 1, many countries around the world have launched satellites for navigation, communication and observation. Currently, about 3,000 satellites are operating in space around the planet. The importance of space surveillance technology has recently become acute, as the possibility of falling cosmic debris and cosmic collisions has increased, due to the increase in artificial space objects.
In case of collision risk, orbit and attitude dynamic information of target satellites should be analyzed, but debris and defunct satellites cannot obtain accurate information because the mission is terminated. In this study, spin period and spin axis are analyzed to obtain attitude information of defunct satellite through photometry observation.
Attempts to study satellite attitude using SLR started with the spin period analysis of LAGEOS-1, a geodesic satellite. Later in 2013, a study to determine the spin axis was conducted using the Ajisai satellite, a spherical satellite consisting of regularly arranged reflectors (Kucharski 2007). For Ajisai, the distance of each reflector changed when observed with high-repeat SLR. This allowed us to see how tilted the satellite was (Kucharski 2010). And in 2017, the spin period and axis of the defunct TOPEX/Poseidon satellite were determined using SLR observations (Kucharski 2017). For using SLR, satellites must be equipped with retro reflectors, and SLR systems need expensive and precise technology. On the other hand, Photometry is relatively simple and does not require retro reflectors. Therefore, we attempted to study satellite attitude by analyzing the spin period and axis of satellites using only photometry obserbation.
The defunct GLONASS satellite, which has completed its operating life, cannot control its attitude relative to the ground, and estimating its attitude is also difficult. Because the orientation of the satellites it is not being controlled, the solar pressure force received from the sun changes depending on the attitude of the satellite, so understanding its attitude and spin period are important (https://nssao.or.kr).
In this paper, we determined the spin period of the defunct GLONASS satellite using photometric observations. We simulated the amount of sunlight the satellite receives and compared it with the observed light curve to find the spin axis and study the satellite’s attitude.
To accomplish this we tracked the Earth-orbiting defunct GLONASS satellite and use a photometer to measure the light reflected by the satellite. The unique spin period of a satellite can be analyzed using the light curve obtained from measured photon counts. We then used the Lomb-Scargle algorithm (Lomb 1976;VanderPlas 2018) Fourier transform, which changes the time domain function into a continuous frequency domain function. This algorithm is known to detect and characterize periodicity in unevenly sampled time arrangements. With this algorithm, photon count data can be used to analyze the spin period of satellites (Spin axis).
The orbit of the GLONASS satellite was calculated from the TLE data. A coordinate transformation matrix using the spin rate and axis information was used to determine the geometric relationship between the observer and the sun from the satellite center.
A model (including surface, area, reflection) similar to GLONASS was used, based on the Box-wing form. In the phase function, the phase of each satellite face can be obtained by using the satellite-observer, satellite-solar relation and reflection information over time. Based on the obtained phase values and area information, we can determine how much the satellite reflects sunlight using the irradiation function. By comparing these simulations with photometry data, Ra, Dec are adjusted; Spin axis is calculated using distance square minimum method.
The goal of this study is to improve orbit accuracy by analyzing satellite attitude, by determining the spin period and axis of the satellite using just photometry, and then including the attitude information of the satellite and its effect on the external solar force received in the orbital information.
2. METHODOLOGY
Satellites that have completed their lifespan orbit about the center of the earth and rotate about the center of their satellite mass. Each satellite has a different spin period, and determining that period is essential to analyzing their attitude.
The spin period analysis is performed using a light curve obtained by observing GLONASS using a photometer. This light curve represents the number of photons entering the photometer for time, and it shows regular pattern. In this light curve, we can see that the peak points have a constant interval.
The Lomb-Scargle method is a method of estimating spectral density. Fourier analysis is the most common signal analysis method, but it is not suitable for photometry data analysis with uneven sampling time series. Photometry observation receives an uneven time interval optical signal due to atmospheric extinction and the spin of the satellite. Since the Lomb-Scargle method can be applied to nonuniform sampled time series, Lomb-Scargle is more suitable for spin analysis of photometry data than fourier analysis (Lomb 1976;VanderPlas 2018).
Space objects rotate not only with a spin period but also with a unique spin axis, and the way they rotate depends on the degree to which the spin axis of the object is tilted. Normally, as the satellite performs its mission, it orbits in a stable position, but when its life span is over, the spin axis and period shift slowly.
To define the spin axis of a satellite, it is essential to analyze the geometric relationship between the satelliteobserver and satellite-Sun in the satellite-centered coordinate system. For this relationship analysis, we first analyzed the orbit of the satellite in the observer center coordinate system using the SGP4 algorithm in Earthcentered inertial coordinate systems (ECI). SGP4 is a mathematical model that is critical to calculating the orbits of satellite and space debris relative to the ECI coordinate system. This SGP4 model predicts the effects of perturbation caused by the shape of the Earth, its drag, and the gravitational effects of other celestial bodies, such as the Sun and the Moon. The GLONASS satellite, which is the subject of this study, is given NORAD’s TLE, so SGP4 is available (Vallado 1965, 2006). The ECI coordinate system is a coordinate system that is based on the center of mass of the Earth. The X-axis is directed at the vernal equinox, and the Z-axis is defined as the axis of rotation of the Earth.
The relationship between the observer-satellite and the Satellite-Sun obtained through this algorithm is converted into a satellite-centric coordinate system using a coordinate transformation algorithm. A brief figure of coordinate transformation from ECI to body-centered coordinate systems (BCS) is as shown in Fig. 1.
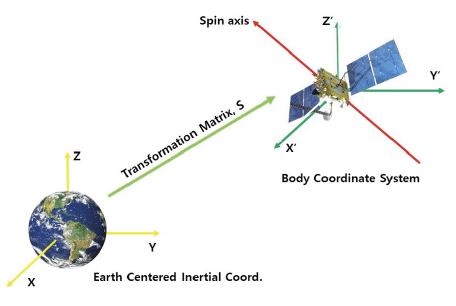
Assuming that the spin axis of the satellite always matches the symmetric axis of the satellite, it changes according to the transformation matrix S as follows (Seeber 2003).
Amomg the variables constituting matrix S, α represents the Right Ascension of the satellite spin axis, δ represents the Declination of the satellite spin axis, and γ represents the spin angle. The spin axis (RA, Dec) of the GLONASS satellite is defined by the observer reference coordinate system.
Vectors from ground observation stations to the satellites and the sun are converted from ECI to BCS through a reduced transformation matrix from the top. The BCS coordinate system refers to the satellite body, it is satellite body fixed and centered at the satellite center-of-mass. So it rotates with satellite body about the satellites spin axis which defines +ZBCS axis. All coordinate systems are defined as the right-handed Cartesian. The coordinate system transformation equation is as follows.
Now it is necessary to model the size of the GLONASS, which is a first generation satellite, and consider the box-wing form. The detailed specifications for the first generation of GLONASS follow in Table 1 (Rodríguez Solano 2014).
The GLONASS to be simulated was modeled using these specifications, and a phase function was used to analyze the phase of each side of the satellite. Because each satellite has its own particular specification, the GLONASS model was used (Milani 1987).
where A is the facet of the exposed satellite surface which follows the Box-wing model: I⨀ is the solar light, and is the distance between the observer position and the satellite center. The ψ is the value obtained from the phase function. The phase function is as follows (Frueh & Jah 2014).
Among the variables used in this equation, β´ is the angle between the radiation direction and the normal vector, γ´ is the angle between the observer and the normal vector, Cd is the diffusion reflection coefficient, and Cs is the regular reflection parameter, where Cd follows the reflectivity of the Box-wing model. The δ is the angle between the sun and the observer from the satellite center, the reason why δ should be greater than 0.25 in the condition that τ is given as 1 is the angle that the observer can see while reflecting the sunlight as the satellite orbits. The value used to determine τ is:
is the observer direction from the satellite center and is the solar direction. In this process, the phase value for each side of the satellite is obtained, and the irradiation at the observer position can be obtained.
Here, the irradiation of the entire satellite can be obtained by using the irradiation observed for the area of the satellite.
The parameters (RA, Dec), which constitute the simulated irradiation values, are compared with the photon counts plot while coordinating. The method for comparing the simulation and light curve to determine the spin axis was calculated using the square of the distance of the corresponding peak points by adjusting the variables (RA, Dec) in the coordinate transformation matrix and calculating the point where the sum was minimum using the spin axis.
The least squares approximation, a method of approximating the liberation equation of a system, is a method of finding a solution that minimizes the sum of the squares of the error of the actual solution and the approximation. This method can be useful when the value cannot be accurately measured, and is used to estimate constant values of the equation, especially when the equation of the system knows what form it is.
The biggest factor affecting the spin period and axis of the satellite is solar radiation pressure, whose momentum is given by the photon energy divided by the speed of light. When photons from the sun strike the satellite, they are absorbed into the specular or the diffuse mode or reflected, and the momentum of the satellite is affected. The basic force vector dF caused by the surface element dS of the satellite by the incident photon flux is given by: (Milani 1987).
where c is the speed of light, ρ is the reflected incident light, and σ is the diffused incident light. is the surface normal vector, β is the radiation source, the vector toward and the angle with n. Here, ρ and σ follow the reflection and diffusion specifications in the Box-wing model.
The photon flux considered in this rotation simulation is direct solar radiation ΦSUN. ΦSUN can be calculated as follows.
The solar radiation constant is S’ = 1,361 W/m2, and the Earth shadow function φ is 0.1. AU is an astronomical unit, and r0 is the solar-satellite distance in AU.
Space objects are powered by solar radiation as they orbit and rotate. To simulate how much power space objects receive from the sun, specifications for the dimensions, masses and optical properties of the object are required. The characteristics of the surfaces that make up each satellite are all different, so the degree of sunlight received by each side is different. The specifications of the target GLONASS-50 satellite in this study follow Carlos’ paper.
3. DATA PROCESSING AND ANALYSIS
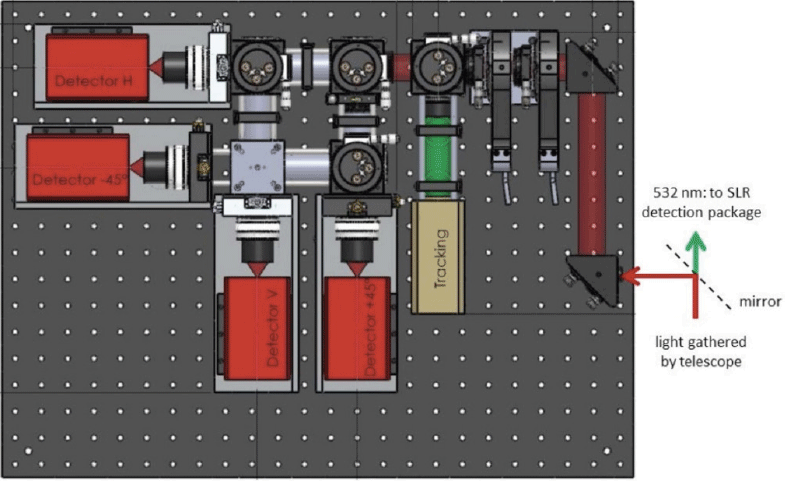
To study the attitude of the defunct GLONASS, we observed the phase GLONASS, which was completed on 2017, at the Austrian Academy of Sciences in Austria Graz. The location of the Graz Station was (4,194,511.7 m, 1,162,789.7 m, 4,647,362.5 m) posted on the ILRS Network in ECEF. Graz Station has been conducting a satellite rotation study using high-repeat rate SLR with kHz performance. However, SLR tracking is only possible if the satellite is equipped with a reflector visible to the observer. Since 2015, Graz has begun researching the simultaneous use of SLR and a photometer for satellites receiving sunlight, and has begun studying the attitude of satellites using the obtained light curve.
The photometer used for the defunct GLONASS observation at Graz Station consists of 4 single-photon detectors and has a 780–1,000 nm spectral detection range. The GLONASS, which is a bright target, was observed at 50 kHz with this photometer; Fig. 2 shows the photometer used for the observation.
Using the top light curve plots, we can see that the defunct GLONASS satellite has regular patterns and have similar peak points with time intervals. The periodogram with power spectrum show the power according to the cycle. The power value is high in the area where the satellite’s own period is likely. The information observed for each GLONASS satellite is shown in Table 2 and light curve shown in Fig. 3.
The photon counts data observed by the photometer, are displayed per second per day. The periodogram of the power spectrum calculated using the periodic analysis algorithm is shown in Fig. 4.
Defunct GLONASS satellite was observed by photometer at Graz Station and the spin period was analyzed using the Lomb-Scargle Algorithm (Lomb 1976;VanderPlas 2018). The 4 Peaks in Fig. 4 represent the periodic power of the GLONASS-50 satellite; the 41 sec with the highest power is the period of the satellite. The largest peak is the largest part of the satellite’s surface reflected in the sunlight, and the remaining 3 peaks are the surfaces of the lesser satellite.
The first generation of GLONASS satellite ended their navigation missions long ago, and their spin period would have been changed by various factors, such as solar radiation and collisions with space objects. The above Periodogram shows that the period of the GLONASS-50 satellite has the greatest power at 41 sec. Since the same area is seen twice while the satellite rotates once, the satellite has a period of 82 sec.
Two line elements data for specific dates for the GLONASS satellite was then obtained from Space-Track. Using David A. Vallado’s SGP4 (Simplified General Perturbations 4), the location of each satellite was obtained from the Earth Centered Inertial Coordinate System(Vallado 1965;Vallado 2006). The altitude of the satellite and the sun were obtained by converting from the Earth-centered inertial coordinate system of the Graz ground station into the observer-centered coordinate system is equal to Table 3. According to the table, the altitude of each GLONASS satellite at the time of observation was between 72.7°–76.5°. Satellite was located above the solar altitude, and the distance from the Graz ground station to the GLONASS satellite was 19,306 km.
Using equation (2) the geometric relation between the observer obtained from the previous and satellite and sun, the coordinate transformation is done in the earth central inertial coordinate system to the satellite central coordinate system. The reflection rate of the Box-wing model in Table 3 was applied to the geometric relationship between the observer and the sun obtained from the satellite center coordinate system, and the phase reflection of each surface of the satellite was analyzed using equation (4). The next Fig. 5 represents the phase reflection of the GLONASS-50 satellite over time. The legend with phase of 0.2 or less is the phase value corresponding to each side of the satellite, and the combined phase value of the surfaces of the satellite is between 0.2 and 0.8. The figure shows a constant pattern. There are more than 0.7 primary peak points and 0.3 or more secondary peak points. Fig. 5 indicates the GLONASS-50 satellite has a RA of 116° Dec at 92° at body centered coordinate. The RA and Dec values of the applied spin axis are unique solution.
The phase value obtained here and the area of the Boxwing model in Table 1 were applied, and the irradiation of the entire satellite was obtained using equation (3).
The next Fig. 6 represents the irradiation of the satellite according to observation time. The unit of irradiation is W, and the patterns ranged from about 3.4 W to up to 5.3 W. Like the phase value, it was possible to check the primary and secondary peak points.
To determine the spin axis, RA and Dec, which are the variables used to convert coordinates to the satellite central coordinate system, were coordinated and compared with the observed light curve. The simulation and light curve comparison method calculated the minimum part by spin axis by summing the square of the distance from the peak points shown in each. The next Fig. 7 is the minimum distance ratio around RA and Dec, assuming the sum of the distance squares is 1. The top peak points in Fig. 6 show that the value is becoming lower and lower, and the bottom peak points show that the difference between the maximum and the minimum is getting bigger and bigger. This study compared with light curve data using these characteristics.
A simulation of the GLONASS-50 satellite was performed, and the results were analyzed using formula (6) to determine how much photon radiation pressure was received from the sun. In this equation, and were used in the Box-wing model, respectively, for diffusion and reflection.
Fig. 8 defines the angle between the sun and the satellite as elongation, focusing on the Graz Station, and shows the force received by the satellite moving in the long-track direction in N. The GLONASS-50 satellite was powered up to 2.328 × 10–5 N at a minimum 3.033 × 10–6 N during the observation period.
4. CONCLUSIONS
Defunct GLONASS satellite is uncontrollable and has no information, which can cause collisions with other space objects. So, this study analyzes the attitude of the satellite, determines the spin period and axis of the satellite using only the photometry observation, and improves the orbit accuracy by including the effect on the attitude information of the satellite and the external solar power received from the orbit information.
Four single-photon detectors in the Austrian Academy of Sciences in Graz, Austria were used. The defunct GLONASS satellite was observed at 0.01 second intervals on Jan 2017.
First, the observed photon counts data was analyzed using the Lomb-Scargle Algorithm which applied a Fourier transform. The spin period of the satellites was 88.22 sec.
The phase reflection of each surface of the satellite was obtained by converting the satellite-centered coordinate system from the observer-centered coordinate system required to determine the spin axis, and then applying the reflectivity of the box-wing model.
The satellite models were fabricated using the phase value and the area information from the box-wing model. After that, the necessary variables (RA, Dec) were coordinated in the process of coordinate transformation, and the spin axis was determined by comparison with the observed light curve. The method of comparing the simulation and light curve defined the point that the sum of squares of distance with each peak point is the minimum as spin axis. The spin axis of the GLONASS-50 satellite was RA = 116°, Dec = 92°. The irradiation of the satellites showed regular patterns between 3 × 10–12 W and 5 × 10–12 W during the observation time, and the maximum irradiation value was gradually decreasing.
In future studies, we will analyze the difference in precision by calculating the spin period axis using simultaneous observations with SLR and photometry, and study how the spin axis changes through long-term observation.








