1. INTRODUCTION
Autonomous rendezvous docking technology is based on the analysis of relative motion between objects in space (Clohessy & Wiltshire 1960). Since it is an essential technology for large-scale missions based on deep space exploration, including lunar and asteroid exploration and space travel, as well as formation or constellation missions, orbital servicing missions such as satellite repair and refueling, and direct removal of space debris, the mission based on it have been continuously developed from the beginning of space exploration to the latest research.
The NASA’s demonstration of the autonomous rendezvous technology (DART) mission (Rumford 2003) launched in 2005 was aimed at carrying out autonomous rendezvous- docking maneuver based on the target satellite, the Multiple Paths, Beyond-Line-of-Sight Communications (MUBLCOM) satellite. However, the satellite’s GPS receiver offset caused a collision with the MUBLCOM satellite and failed to achieve its purpose. The Experimental Satellite System-11 (XSS-11) launched in 2005 was developed by the U.S. Air Force Research Laboratory to demonstrate capabilities and technologies of autonomously rendezvous and proximity operations in micro-satellite (AFRL 2005). The NASA’s Orbital Express mission (Friend 2008) launched in 2007 consisted of two satellites (ASTRO satellite for servicing, NEXTSat satellite for serviceable satellite). The goals of this mission were developing autonomous on-orbit servicing of a satellite, including rendezvous, refueling, capturing another satellite using their robotics. At the same time, in Europe, though the Prototype Research Instruments and Space Mission technology Advancement (PRISMA) in 2010, autonomous formation flying, proximity operations, and rendezvous technologies for on-orbit servicing were demonstrated (Gill et al. 2007). After the DART mission in 2003, the mentioned rendezvous-docking technology demonstration satellites successfully completed the mission.
However, there were disadvantages of high cost and high risk due to the size of satellites and the development period of past missions. To compensate for this, the number of technology demonstration and development cases using nanosatellites that can be developed at a low cost and for a short period of time is increasing in recent research. The Surrey Training Research and Nanosatellite Demonstrator (STRaND-2), developed by Surrey Space Center in 2013, verified rendezvous-docking technology using two 3U CubeSats and established a docking system using magnetic coils (Bridges et al. 2013). The On-orbit Autonomous Assembly of Nanosatellite (OAAN) Project, conducted by NASA Langley Research Center in 2015, aimed at creating rendezvous-docking technology based on nanosatellite. In this project, two 3U CubeSats were used, like the STRaND-2 mission, and the autonomous rendezvous-docking control using carrier-phase differential (CD) GPS was to be verified (Murchison et al. 2015). Developed by Tyvak, The CubeSat Proximity Operations Demonstration (CPOD) mission aimed to carry out the rendezvous, proximity operations, and docking by applying components suitable for CubeSat using a pair of 3U CubeSats (Roscoe et al. 2018). And now, Korea Aerospace Research Institute (KARI) a Rendezvous-Docking technology demonstration SATellite (KARDSAT), is being developed by the KARI. The chaser in KARDSAT detects the target through the image data received through the vision sensor of the chaser with the developed deep learning algorithm mounted on the onboard. Based on the image data, the rendezvous-docking phase is performed through the relative position and attitude data. At the end of the docking phase, after undocking, the drag sails mounted on the target are unfolded and the chaser uses the remaining fuel to re-enter the Earth, end the mission (Kim et al. 2019).
However, among the aforementioned nanosatellite-based projects, the probability of success in the space environment is extremely low due to limitations such as the weight, size, and power of the satellite itself, etc. Indeed, as far as the author’s knowledge, it is hard to find the development of simulators for rendezvous-docking mission. A paper related to rendezvous-docking simulation in the nanosatellite environment through NASA Simulation Environment (Trick, JEOD) and C++ library (Armadillo) (Fear 2014), but not developed as a GUI, and the use of commercial tool GNCDE was used for large satellites (Strippoli et al. 2016).
Therefore, in order to ensure the success rate of the KARDSAT mission, and for a relatively light and user-friendly compared to previous studies by using an accessible MATLAB® code docking phase analysis tool were developed. The tool performs relative position and attitude control analysis of the chaser satellite during the docking phase in the mission. It is largely divided into three parts, consisting of a satellite’s Dynamics, Kinematics and Environment (DKE), controller, and filter about sensor noise. Satellite DKE library is the MATLAB® library within commercial GNCDE tools, (Strippoli et al. 2016), Model Predictive Controller (MPC) is used as a controller (Camacho & Bordons 2004), and Kalman Filter is used to filter the sensor noise. Although the commercial tool was intended to be used, MPC decided that it was appropriate to apply the constraints of the rendezvous-docking phase, so the Proportional-Derivative (PD) controller of the commercial tool was changed to MPC, and only the satellite DKE model library was used.
MPC stands out in a recent rendezvous-docking mission study because of its advantages in setting constraints and cost function according to purpose and predicting future state of the system. Park et al. (2011) and Kannan et al. (2016) applied MPC to debris avoidance. In Gavilan et al. (2012), to deal with the disturbance in the rendezvous phase, a robust MPC modeled as a chance-constrained approach was used. In (Leomanni et al. 2014), MPC was used for low-thrust spacecraft proximity operations. Case studies in Farahani et al. (2016) and Weiss et al. (2015) were conducted on the initial phase per maneuver between the two satellites.
In the rest of the paper, in Section 2, we discuss the modeling for relative motion of satellite, MPC and EKF. In Section 3, we present the GUI configuration, input parameters and output. The setting of parameter and the result of the case study is shown in Section 4 and the conclusions and future works are summarized in Section 5.
2. MODELING
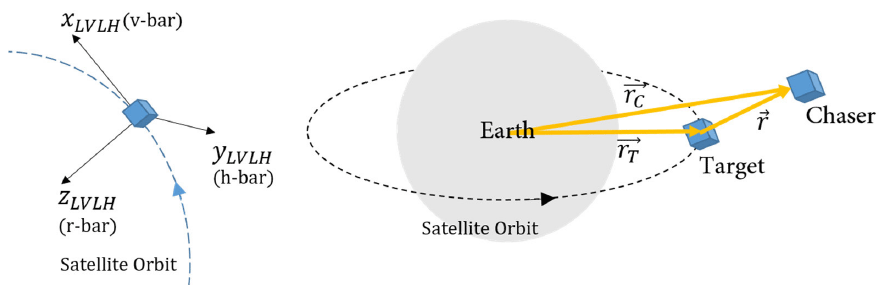
To express the relative motion between the chaser satellite (chaser) and target satellite (target) in the rendezvous- docking phase, we will introduce the Clohessy- Wilshire-Hill (CW) equation (Clohessy & Wiltshire 1960). We have set up the target is in the center of the local-vertical- local-horizontal (LVLH) frame, the relative position vector of chaser with respect to the target is expressed as Fig. 1 shows the chaser and target in the LVLH frame. The linearized CW equation can be derived assuming a target with a circular orbit and the distance between the two satellites is negligible relative to the distance from the Earth Under the assumptions, the state-space model of linearized CW equation can be used for the relative motion expressed by Eq. (1),
where , is the relative states for the chaser, is the external force of the chaser, and
is the angular rate vector of the target, where μ is the gravitational constant. And, the superscript P means the position and is used for expression about the equation of position control. The GNCDEⓇ Dynamic, Kinematic and Enviroment (DKE) library for rendezvous- docking simulation is used for this modeling.
To perform chaser attitude control, the satellite attitude dynamics and kinematics of the chaser are imported as follows (Markley & Crassidis 2014),
where is the inertia matrix of satellite, 3 is the angular velocity of satellite, is the control input (torque of the satellite), is the attitude quaternion of satellite, and
To express Eq. (4) as a state-space model, by discretizing
where Δt is the sampling time, wA(k) is the error resulting from the Taylor series in the discretizing process and XA(k) = q(k) is the attitude quaternion. The superscript A means the attitude and is used for expression about the equation of attitude control.
MPC predicts states or outputs through models of plants under control and implements optimization using cost functions and constraints in the prediction horizon N. The result of the optimization is the control input, which is obtained by the minimization of the cost function J subject to constraints. During the optimization process, the input or status variable is used in rendezvous-docking missions with constraints on the state because it allows for compliance with the constraints in the form of inequality. The coding for MPC was based on the Yet Another LMI Parser (YALMIP), which is a toolbox for modeling and optimization in MATLAB Ⓡ developed by Lӧfberg (2004). This toolbox can be easily applied to optimal control using optimization solvers such as SeDuMi, SDPT3, and Gurobi, etc., and is being updated to date.
About the MPC of relative position, referring to Park et al. (2011), in order to apply Eq. (1) to MPC, it should be represented by a discrete-time model Eq. (8).
where are the discrete-time matrix of of (1), are state and input vectors at the sampling time instant k.
The cost function JP is designed based on LQ problem, and constraints for the tool are designed as follows,
subject to
where QP, RP are the weight of the difference between the reference value and state, the weight of the control output value, both of which are positive definite diagonal matrices, is the reference of 6 state vectors, which is the position (x, y, z) and velocity vector of docking port of the target with respect to the target. , is the docking port position and velocity vector of chaser with respect to the target, and NP is the prediction horizon for position control.
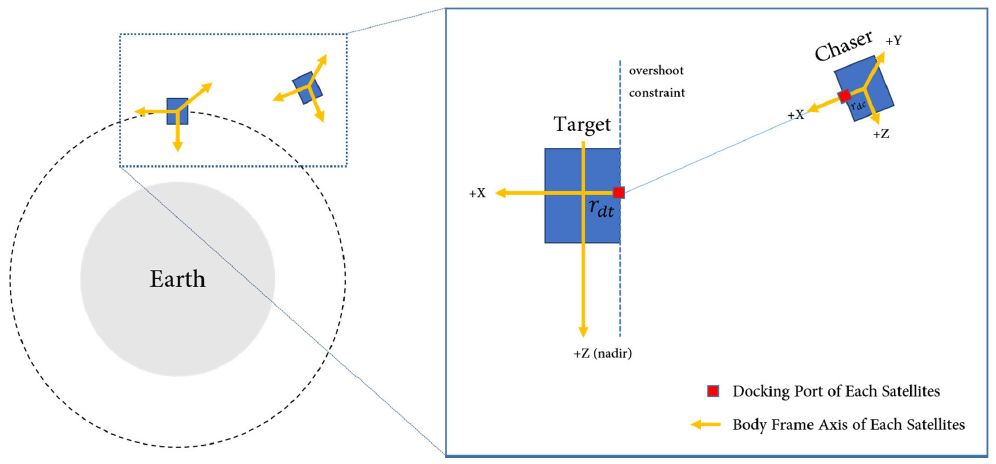
Fig. 2 shows the constraints of the simulation tool. The constraint Eq. (10) follows from Eq. (8), Eq. (11) is the overshoot constraint for observability of sensor and is the x-axis position state of the docking port of target. Because the chaser must always keep an eye on the target, the chaser’s position should always be located behind the target. The constraint Eq. (12) is the fuel limitation for fuel efficiency.
The controller of attitude control is used PD controller. PD control is performed using the distance between two satellites as a reference for the attitude control. When the distance between the two satellites is farther than the existing distance, the chaser attitude quaternion enables the chaser to continuously observe the target because the sensor mounted to the chaser continues to direct the target. In order to continuously observe the target, the LoS vector of the vision sensor mounted on the chaser was set as the vector to which the chaser faces the target. To apply this setting, we set the chaser body frame that aims at the target. When the distance is greater than the reference distance, control is performed to maintain the chaser body frame in the target. To set the chaser body frame, it is assumed that the sensor is mounted on the x-axis of the chaser body frame, and the body frame x-axis and the sensor LoS vector are set to be the same. Through this assumption, the axis of the set chaser body frame is as follows (Woffinden 2004;Woffinden 2008).
where uPD is the torque of chaser, which is the output of PD controller, qcom, ωcom is the command of quaternion and angular velocity, is the location value of the body frame with respect to the inertial frame.
Extended Kalman Filter (EKF) is adopted as a noise filter for on the vision sensor for the rendezvous-docking. EKF is a filter that linearizes a nonlinear model to predict future state values through measurements and past state values in the same format as the Kalman Filter. The model we used is the linearized model described in 2.1 and 2.2. The linearized CW equation to EKF can be found in various literature. In Woffinden (2008), the autonomous relative navigation was studied for each maneuver with the measured angle. And, relative angles-only navigation between satellites by coordinates was studied in Pi (2011). We present which models and parameter values are used for relative position and attitude control in this section.
We need the process model and the measurement model of the relative motion, so we implemented linearized relative equation Eq. (1) and linearized attitude equation Eq. (7) for the process model. And, for measurement equation, we assumed the relative position, velocity and quaternion, angular velocity is measured with respect to the target. So, the measurement model is same the measurement model. The noise standard deviation of measurement model is determined as 1% of the true value, as measured values using image and deep learning algorithm, so it is time-varying covariance.
3. METHODOLOGY
Fig. 3 is the configuration of GUI. This analysis tool is designed to analyze the relative position and attitude control of the satellites in the rendezvous-docking mission. And, the satellites’ initial state and structure, the disturbance coefficient with the satellite, the controller gain, and the simulation setting values are set as input parameters. Output values after simulation can be saved as figures by data- driven or graphically stored on the user’s computer. The analysis tool’s flowchart is described in Section 3.1.1, and the detailed input parameters and outputs of the analysis tool are presented in Section 3.1.2.
Fig. 4 is the flowchart of the control analysis using the developed tool. When the GUI is turned on, the optimization toolbox (YALMIP) is set up together. And, when you enter the parameters of the satellite, and press the APPLY button, it is applied to the linked to Simulink file of analysis tool in MATLAB®. At the end of the analysis, the outputs of analysis are stored in the workspace of MATLAB®. This output can be saved in several file formats via the buttons of SAVE panel. Data files can be saved multiple file formats with DATA button, setting parameters for simulation can be saved with PARAMETER button, and a plot image can be saved with PLOT button by floating figure. In addition, through ‘Plot’, the data analyses through the several graph are available.
3.1.2 Input Parameters and Output Data
The input parameter is as follows,
Chaser initial values include initial position and velocity with respect to inertial frame, mass, initial angular velocity, initial quaternion with respect to inertial frame, docking port position with respect to chaser body frame. Target initial values include initial position and velocity with respect to inertial frame, mass, position of docking port with respect to target body frame (LVLH). The parameters about disturbance include the flags of aerodynamic drag, solar radiation pressure, moon and sun attraction, nonsphericity of the Earth, the coefficients of aero drag, reflectivity, the surface affected by solar and aerodynamic drag.
The parameters of satellite structure include the satellite area per body frame axis (SC Area), the solar array per body frame axis (Solar Array Area).
MPC parameters (Position control) include predict horizon N, positive definite diagonal matrices Q, R, and acceleration limit Umax, Umin. PD controller parameters include natural frequency, damping ratio, and torque limit Umax, Umin.
Simulation setup parameters include required range between two satellite, relative velocity, and simulation time. The white box is a marker that shows the simulation is over by changing color.
The output values include simulation time, chaser/target position with respect to inertial frame, chaser/target velocity with respect to inertial frame, chaser position/velocity with respect to target frame (LVLH frame), quaternion of chaser/ target with respect to inertial frame, quaternion error between chaser and target, estimation of position of chaser with respect to target, estimation quaternion of target with respect to inertial, angular velocity of chaser, force of chaser, torque of chaser, ΔV of chaser, and total ΔV of chaser.
4. RESULT
In the simulation, it is assumed that the initial status of two satellites is in the beginning stage of the docking phase. So, the two satellites in the inertial frame have the same initial velocity and so that the relative velocity of the two satellites is zero, which is two satellites are in stationary status. For the initial condition, the initial velocity in the inertial frame of the two satellites is left equal, assuming an initial relative velocity of zero. This is when the chaser is stationary in the LVLH frame. Under this assumption, parameters setting is made.
In this section, the two cases of simulations are informed, which shows the cases for the two initial positions of the chaser. Table 1 and Fig. 5 are the fixed parameters value for simulations. Simulations are performed when two satellites are aligned on the x-axis of LVLH frame and when they are not. In the first simulation when the two satellites are aligned on the one axis, the initial position and velocity in the inertial frame of the chaser is [6828447 –6.113 –7.8374] m, [3.96 4745 5987] m/s. And, the chaser initial position and velocity in the inertial frame in the second simulation, which are not aligned on one axis, is [6828447, –0.133, –10.17] m, [3.96 4745 5987] m/s.
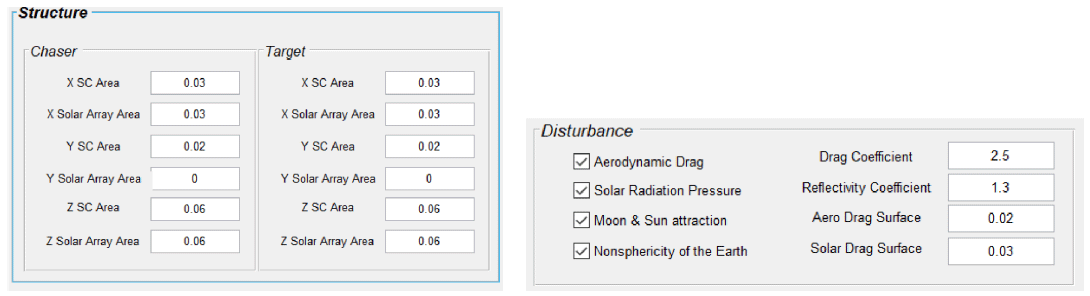
Fig. 6, Fig. 7 show the position and velocity of the chaser in the LVLH frame (relative position between two satellites), the cumulative graph of total ΔV of the chaser, and the quaternion error between two satellites. (from left to clockwise) In the relative position graph of both simulations, the relative position is converging on the docking port position [–0.2, 0, 0] m, which is the value of the control reference. The relative velocity graph shows converging at the reference velocity [0, 0, 0] m/s after a large change from 0 second to 1,000 seconds. And, the accumulated total ΔV graph is shown for analyzing the fuel used by the chaser. In these graphs of the two simulations, the total ΔV values at the last stage of the docking phase are 0.122 m/s, 0.055 m/s, it is expected that less fuel from the chaser will be used in the second simulation. Finally, from the quaternion error graph for attitude control analysis of the chaser, we can see that the error value decreases as the quaternion of the chaser fol-lows the quaternion of the target from the time the distance between two satellites reaches the threshold. (Fig. 6: 1,800 secs, Fig. 7: 1,700 secs) The threshold is set to 1 m between the center of the body frame of the two satellites.
Since the environment for this simulation is assumed to be nanosatellite, the force, the orbital control input of the satellite, is limited for low-thrust satellite. Therefore, the simulation is run with a limited value of Umax = 4 mN, Umin = –4 mN during attitude control for low-thrust. Fig. 8 show the force of the chaser, which is the control input in each simulation. In the whole graph, the force of the chaser is not exceeded the limit of force. Through this graph, we can see that the x-axis (top of graph) and y-axis (middle of graph) of LVLH frame have fewer force values in the second case than in the first simulation, which is the same as expected result of the total ΔV graph in Fig.6 and Fig. 7. Through this result, it is judged that the second case in an unaligned state is more suitable for low thrust.
5. CONCLUSIONS AND FUTURE WORKS
In this paper, a tool for analysis of control of rendezvous- docking phase in nanosatellite was developed using MATLABⓇ, and GNCDE library of GMVⓇ. The tool was applied MPC for orbital control, PD controller for attitude control, and EKF for estimation of values added noise. The simulation identified how the tool works, and the resulting graph showed that orbital control and attitude control for satellite were successfully implemented. Therefore, using this tool, the mission success rate will be increased by conducting a rendezvous-docking simulation under the nano-satellite environment. And, in this paper, the simulation of the docking phase was performed, but it can be used in various scenarios such as the rendezvous phase depending on the parameters to be set by the user. And by implementing various sensor models used in real missions, it is possible to build a system more suitable for real models, and analysis by satellite size (or mass) is expected to be possible.




