Journal of Astronomy and Space Sciences

The Korean Space Science Society

2020; 37(3):171-185

pISSN: 2093-5587, eISSN: 2093-1409

DOI: https://doi.org/10.5140/JASS.2020.37.3.171

Research Paper

Determination of Orbital Elements and Ephemerides using the Geocentric Laplace’s Method

Daniela Espitia†

, Edwin A. Quintero

, Ivan D. Arellano-Ramírez

Grupo de Investigación en Astroingeniería Alfa Orión, Observatorio Astronómico, Universidad Tecnológica de Pereira, Complejo Educativo La Julita, 660003 Pereira, Colombia

^†Corresponding Author Tel: +57-3163873180, E-mail: daesmo95@utp.edu.co

© The Korean Space Science Society. All rights reserved. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Received: May 14, 2020; Revised: Jul 13, 2020; Accepted: Aug 4, 2020

Abstract

This paper presents a methodology for Initial Orbit Determination (IOD) based on a modification of the Laplace’s geocentric method. The orbital elements for Near-Earth asteroids (1864) Daedalus, 2003 GW, 2019 JA8, a Hungaria-type asteroid (4690) Strasbourg, and the asteroids of the Main Belt (1738) Oosterhoff, (2717) Tellervo, (1568) Aisleen and (2235) Vittore were calculated. Input data observations from the Minor Planet Center MPC database and Astronomical Observatory of the Technological University of Pereira (OAUTP; MPC code W63) were used. These observations cover observation arcs of less than 22 days. The orbital errors, in terms of shape and orientation for the estimated orbits of the asteroids, were calculated. The shape error was less than 53 × 10^–3 AU, except for the asteroid 2019 JA8. On the other hand, errors in orientation were less than 0.1 rad, except for (4690) Strasbourg. Additionally, we estimated ephemerides for all bodies for up to two months. When compared with actual ephemerides, the errors found allowed us to conclude that these bodies can be recovered in a field of vision of 95’ × 72’ (OAUTP field). This shows that Laplace’s method, though simple, may still be useful in the IOD study, especially for observatories that initiate programs of minor bodies observation.

Keywords: asteroids; astrometry; ephemerides; initial orbit determination; laplace method; orbital errors

1. INTRODUCTION

Progress in the acquisition of astronomical images has dramatically increased the available astrometric information of minor bodies of the Solar System. The way to calculate orbits in the last decades has changed (Bowell 1999), so now it is possible to use all this information. This process involves three fundamental stages: an Initial Orbit Determination (IOD) (Marsden 1985), a least squares fitting (Vallado & McClain 2001) and quality control (Milani et al. 2008). Additionally, there are challenges raised by the appearance of digital astrometry. Finding a solution to this problem is of great importance for humanity, in order to discover and characterize, in the least amount of time, minor bodies that imply an imminent risk of collision with the Earth (Aristova et al. 2018).

The pioneers to offer a solution to the problem of IOD were Laplace (Curtis 2014) and Gauss (Gauss 1809;Gauss & Davis 2004;Hwang 2009); however, these methods were conceived just over two centuries ago. Because the acquisition of an astronomical image took a great deal of time, these classical methods were elaborated for that context. At present, a large amount of data can be obtained on an observation night, so these methods must be reconsidered (Klokacheva 1991;Sokolskaya 1997) or replaced by alternate ones. For that purpose, comprehensive reviews of the Gauss & Laplace methods have been performed (Milani et al. 2008;Mirtorabi 2014), or completely alternative methods have been investigated, to calculate a finite set of preliminary orbits for solar system bodies, using the two-body integrals (Gronchi 2004;Gronchi et al. 2010).

These methods are adjusted more adequately to the large amount of astrometric information currently available; namely, they use all possible data (unlike the Gauss method that uses just three (Danby 1962). The use of all possible data permits astronomers to perform a good initial orbit es-timation for the celestial body, even when the observational data covers a very short section of the orbit, that is VSA (a very short arc). This definition is used when the sequence of observations belongs to the same object, or if it can be adjusted to a smooth curve (usually a low-degree polynomial Milani et al. 2005).

On the other hand, in studies such as Quijano et al. (2010), orbital elements of the asteroid 2003QO104 were determined using, principally, a linear interpolation by Lagrange method. However, this methodology does not calculate the temporal derivatives of both coordinates. In other words, an attributable is not computed, and therefore it is not possible to determine either the geodesic curvature or the proper motion, which are essential constants for the development of the method. The term attributable was first introduced by Milani et al. (2001) in order to use it to find identifications of asteroids with known orbits, such identification is called attribution. This definition is very important at the present time in the development of methods for orbital determination, for example, methods developed by (Klokacheva 1991;Sokolskaya 1997) do not use this type of approach.

As mentioned earlier, due to a large number of observations available, it is necessary to resort to new methods that allow the monitoring of minor bodies of the Solar System. For this purpose, modern methods can be used based on the invariants of the motion (Villarraga & Quintero-Salazar 2016) or those that estimate the admissible region in which minor bodies can be found (Milani et al. 2004;Mosquera & Salazar 2019).

However, to give a more straightforward solution when there are VSA observations, it is possible to resort to variations of classical methods, such as Laplace (Milani et al. 2008). In this method, computational implementation is simpler compared to modern methods. Through this method, it is possible to know the orbital parameters of minor bodies. This latter is especially important to observatories that are initiating minor bodies observation programs.

Therefore, the purpose of this paper is to discuss a modification of the geocentric Laplace's method that allows for the use of all available astrometric data of the body in question. Moreover, we show how from this data it is possible to calculate the geodesic curvature value of the trajectory and how we use it to find the topocentric distance. Subsequently, we proceed to find the initial values for the problem of the two bodies, to determine the orbital parameters that describe the trajectory of the object.

Finally, the ephemerides for the subsequent re-observation of the minor bodies under study are estimated. Input data, OAUTP observations [MPC code W63 (Villarraga et al. 2017)], among others, available in the MPC database were used. To validate the results, we made a comparison with the NASA JPL Web-Interface service, both for orbital parameters (obtaining orbital errors for shape and orientation), and for the estimated ephemerides (when determining if the object is recoverable or not from a field of vision of 95’ × 72’).

This article is structured as follows: first, the methodology used in this study to recover minor bodies is described in detail. Next, the proposed methodology is validated by comparing the obtained results with those available in the NASA JPL Web-interface service. Finally, the main conclusions are presented, in which the reliability of the modification of the geocentric Laplace's method, by recovering minor bodies from the Solar System is demonstrated. This is useful even when the input data observations represent short time intervals.

2. MATERIALS AND METHODS

In this section, a modification of the geocentric Laplace's method to estimate a preliminary orbit is presented. The flowchart that illustrates this process is shown in Fig. 1.

Fig. 1. Flowchart of the developed algorithm for Initial Orbit Determination (IOD) using the modification of the geocentric Laplace's method.

Download Original Figure

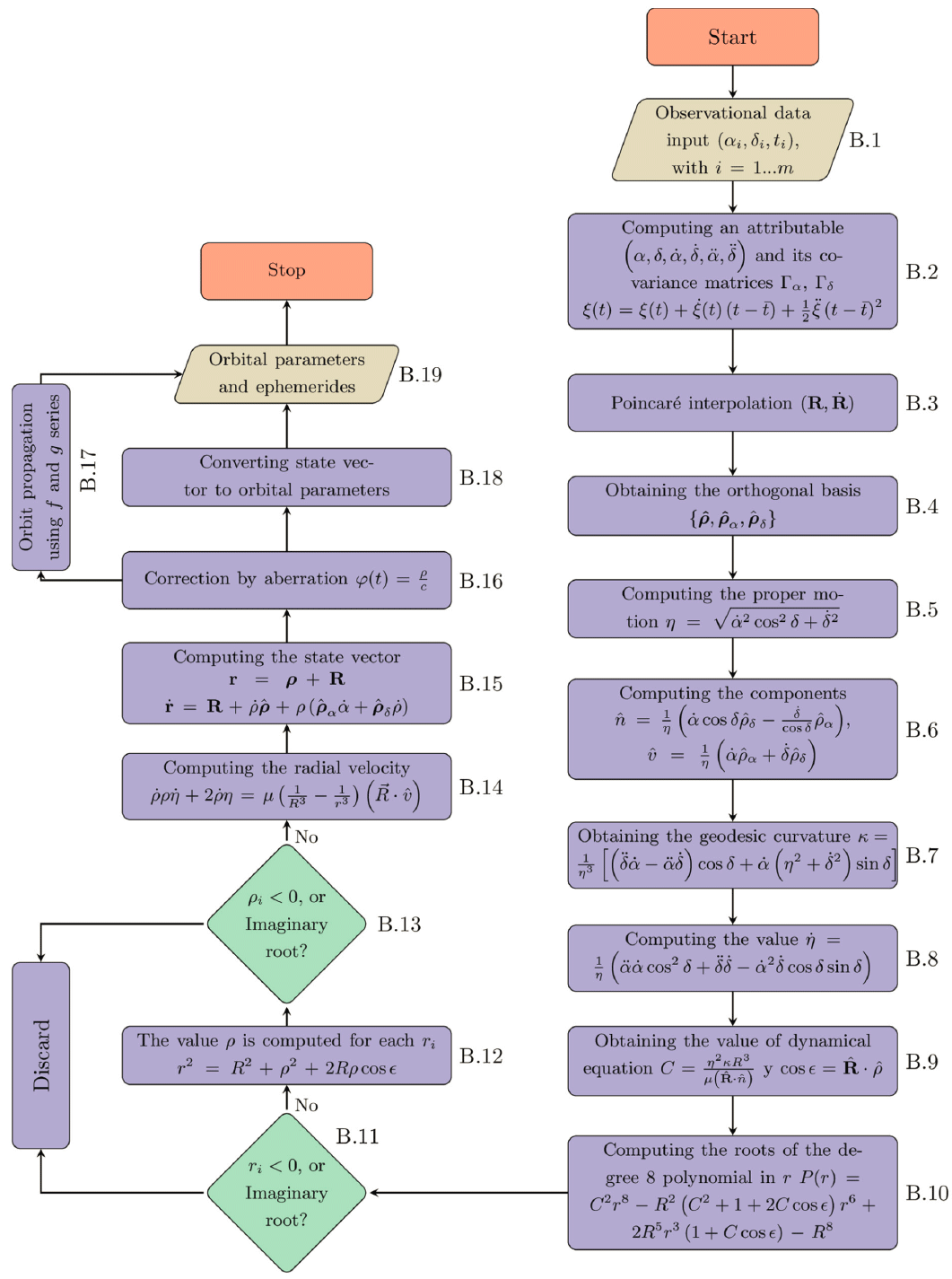
Initially, a minor body $B$ , belonging to the Solar System that moves around the Sun with heliocentric position r is considered. This is observed from Earth ε which has a vector radius R, known for a determined moment of certain time (Fig. 2). The central idea is to find the state vector that describes this trajectory. To achieve this, a least squares fitting to the registered observations is made, and from this, an attributable is obtained. In the next stage, using the same fitting, the state vector of the Earth was estimated.

Fig. 2. Asteroid movement around the Sun and observed from Earth.

Download Original Figure

Furthermore, the methodology involves the calculation of the proper motion, the orthonormal base adapted to the apparent movement of $B$ on the celestial sphere, and the constants of the geodesic curvature and along-track acceleration. Then, the dynamic and geometric equations were applied to find two additional constants that completed the set of constants necessary to estimate the magnitude of the heliocentric position of $B$ . Ultimately, we made a selection of the allowable solutions to find the state vector; with this, it was possible to estimate both the orbital elements and ephemerides. In the following section, methodology is explained in detail.

2.1 Computing attributable

One of the input parameters of the algorithm is the set of astrometric data obtained from different observation nights (Fig. 1, Block 1). Generally these data are expressed as follows:

(t i, α i, δ i) i = 1, …, m

(1)

Where t is the observation time, α the right ascension, δ the declination, where m ≥ 3 is the total number of registered observations.

Then, a polynomial model fitting was performed for an average time t from the t_i (Milani & Gronchi 2010), of the form:

ξ (t) = ξ (t ¯) + ξ ˙ (t ¯) (t − t ¯) + 12 ξ ¨ (t ¯) (t − t ¯) 2

(2)

Where ξ represents the fitting for α and δ, respectively. From these quantities, the attributable vector $A = (α, α ˙, α ¨, δ, δ ˙, δ ¨)$ which is associated with a covariance matrix that yields an estimate of errors (Milani et al. 2001; Fig. 1, Block 2), was calculated.

At this point, the information contained in the attributable A does not include either the value of the topocentric distance ρ or the radial velocity $ρ ˙$ of the body under study. Then, the next step consists in finding the value of such quantities that allow resolving the IOD, determining the orbital elements of a minor body from angular information only.

2.2 Poincaré interpolation

The next step is to estimate the state vector of the Earth (R, $R ˙$ ) , that is, the heliocentric position of the center of the Earth (Fig. 1, Block 3). In order to obtain more precise results, Poincaré (Poincaré 1906;Milani et al. 2008) suggested that these quantities should be calculated consistently with the same interpolation used to calculate the attributable vector and not using exact formulas. Therefore, the position of the Earth for t_i was estimated, and finally, (R, $R ˙$ ) was estimated using the eq. (2). In this case, a geocentric approach was implemented (Milani et al. 2007;Curtis 2014).

2.3 Computing proper motion

Both the position and heliocentric velocity of $B$ are given by:

r = R+ ρ ρ^r ˙ = R ˙ + ρ ˙ ρ^+ ρ α ˙ ρ^α + ρ δ ˙ ρ^δ

(3)

Where $ρ^α = ∂ ρ^∂ α and ρ^δ = ∂ ρ^∂ δ$ .

Being:

ρ^= (cos α cos δ, sin α cos δ, sin δ), ρ^α = (-sin α cos δ, cos α cos δ, 0), ρ^δ = (-cos α sin δ, − sin α sin δ, cos δ)

In the previous set of equations, it is proven that: $ρ^⋅ ρ^α = ρ^⋅ ρ^δ = ρ^α ⋅ ρ^δ = 0 ⋅ ‖ ρ^‖ = ‖ ρ^δ ‖ = 1, ‖ ρ^α ‖ = cos δ$ . The next step of the method is to compute these vectors (Fig. 1, Block 4). Laplace's method is a technique used to approximate the values of ρ and $ρ ˙$ , so that eq. (3) can be determined. Being the topocentric position of $ρ = ρ ρ^$ of $B$ , topocentric velocity is giving by:

d ρ d t = ρ ˙ ρ^+ ρ d ρ^d t

(4)

Using an orthonormal base adapted to the apparent trajectory of $B$ in the celestial sphere, that is, the image of $ρ^(t)$ it follows that (Danby 1962;Milani & Gronchi 2010):

v = d ρ^d t = d ρ^d s d s d t = η v^

(5)

Where s is arc length parameter.

Then, proper motion $η = ‖ v ‖$ was established. Its value is one of the most important quantities that was estimated using the modification of the geocentric Laplace's method (Fig. 1, Block 5):

η = ‖ d ρ^d t ‖ = α ˙ 2 cos 2 δ + δ ˙ 2

(6)

Likewise, the unit vector $v^$ was set, so that:

η = d s d t, v^= d ρ^d s

(7)

2.4 Computing vectors based on the attributable

Now, $ρ^$ has unit magnitude and $d ρ^d s$ is a perpendicular vector to $ρ^$ , so that $v^⋅ ρ^= 0$ . This allows to define a threedimensional basis if the following vector is added:

η^= ρ^× v^

(8)

The mathematical notation of the derivative with respect to s is established as prime; and according to the above relationships, the next properties are satisfied:

v^′ ⋅ ρ^= d d s (v^⋅ ρ^) − v^⋅ ρ^′ = − 1 v^′ ⋅ v^= 12 d d s ‖ v^‖ 2 = 0

(9)

Now, the next derivatives are introduced:

α ′ = α ˙ 1 η, α ″ = 1 η 3 (α ¨ η − α ˙ η ˙) δ ′ = δ ˙ 1 η, δ ″ = 1 η 3 (δ ¨ η − δ ˙ η ˙)

From the second expression in (7), and considering the previous derivatives for the unit vectorv $v^$ , it follows:

v^= α ′ ∂ ρ^∂ α + δ ′ ∂ ρ^∂ δ = 1 η (α ˙ ρ^α + δ ˙ ρ^δ)

(10)

To unit vector $n^$ , the previous expression is replaced in (8), then, the following expression was obtained:

n^= α ′ cos δ ρ^δ − δ ′ cos δ ρ^α = 1 η (α ˙ cos δ ρ^δ − δ ˙ cos δ ρ^α)

(11)

Since eqs. (10) and (11) are in terms of attributable values, the next step is to calculate these values (Fig. 1, Block 6).

2.5 Computing the geodesic curvature and along-track acceleration

According to the properties of (9) vector $v^′$ can be expressed as:

v^′ = − ρ^+ κ n^

(12)

The scalar quantity denoted by κ, is the geodesic curvature, which measures the deviation of the path of a great circle (a geodesic on the sphere). This value is unknown and hence is one of quantities to be resolved.

From the eq. (5) the derivative with respect to time is obtained, and then, replaced into (12), so that:

d 2 ρ^d t 2 = η ˙ v^+ η 2 (− ρ^+ κ n^)

(13)

In this equation, there is one additional scalar quantity $η ˙$ , which was estimated from the attributable as showed latter. To find this scalar quantity the following relationships are considered:

ρ^α α = (-cos δ cos α, − cos δ sin α, 0), ρ^α δ = (-sin δ sin α, − sin δ cos α, 0), ρ^δ δ = (-cos δ cos α, − cos δ sin α, − sin δ)

Where $ρ^α α = ∂ (ρ^α) / ∂ α, ρ^α δ = ∂ (ρ^δ) / ∂ α, ρ^δ δ = ∂ (ρ^α) / ∂ δ$ , and also the following properties are established:

ρ^α α ⋅ ρ^α = ρ^δ δ ⋅ ρ^α = ρ^α δ ⋅ ρ^δ = ρ^δ δ ⋅ ρ^δ = 0 ρ^α δ ⋅ ρ^α = sin δ cos δ = ρ^α α ⋅ ρ^δ = sin δ cos δ

(14)

In order to find κ, scalar product with $n^$ is calculated to both sides of eq. (12):

κ = v^′ ⋅ n^

(15)

Then eq. (10) is derived with respect to s. Simplifying it yields:

v^′ = (α ″ ρ^α + δ ″ ρ^δ) + (α ′ 2 ρ^α α + 2 α ′ δ ′ ρ^α δ + δ ′ 2 ρ^δ δ)

Finally, the previous expression is substituted into (15) and, making the necessary simplifications and substitutions involving (14), an expression for κ is obtained:

κ = 1 η 3 [cos δ (α ˙ δ ¨ + δ ˙ α ¨) + α ˙ sin δ (δ ˙ 2 + η 2)]

(16)

Therefore, from eq. (16), it was possible to compute the geodesic curvature based on the variables of the attributable, which is, as previously mentioned, one of the quantities to be estimated in this method (Fig. 1, Block 7). Otherwise, to find the value of $η ˙$ , the scalar product on both sides of the eq. (13) with $v^$ was performed. Thus we have:

η ˙ = d 2 ρ^d t 2 ⋅ v^

(17)

Finally, using both eqs. (17) and (6), the value for alongtrack acceleration was obtained:

η ˙ = 1 η (α ¨ α ˙ cos 2 δ − α ˙ 2 δ ˙ cos δ sin δ + δ ¨ δ ˙)

(18)

Then, we proceeded to estimate this value numerically (Fig. 1, Block 8).

2.6 Computing constants through dynamical and geometric equations

By replacing (5) into eq. (4), the next expression is obtained:

ρ ˙ = ρ ˙ ρ^+ ρ η v^

Deriving this expression again with respect to time and using (12), yields:

ρ ¨ = (ρ ¨ − ρ η 2) ρ^+ (2 ρ ˙ η + ρ η ˙) v^+ ρ η 2 κ n^

(19)

The two-body dynamic model was assumed in order to obtain preliminary orbits. In this model, the minor body is only affected gravitationally by the Sun; and therefore, no other external force alters its trajectory. Using Newton's Law of gravitation, the heliocentric accelerations of the Earth and the studied body are obtained, respectively, as:

R ¨ = − μ R 3 R, r ¨ = − μ r 3 r

(20)

From eq. (3) it is know that:

ρ ¨ = r ¨ − R ¨ = μ (1 R 3 − 1 r 3) R − μ r 3 ρ

(21)

A scalar product with $v^$ in both eqs. (21) and (19) was performed. The result was equalized, and then the terms were organized as follows:

2 ρ ˙ η + ρ η ˙ = μ (1 R 3 − 1 r 3) (R ⋅ v^)

(22)

This equation shows that if the values of ρ and r are known, the values for velocity $ρ ˙$ can be found. Then, a scalar product with $n^$ ; on both eq. (21) and (19) is performed, this yields:

ρ η 2 κ = μ (1 R 3 − 1 r 3) (R ⋅ n^)

(23)

This expression is organized, and the result is multiplied on both sides by R³, so it is reduced to:

C ρ R = 1 − R 3 r 3

(24)

Where

C = η 2 κ R 3 μ (R^⋅ n^)

Eq. (24) is known in literature as dynamical equation (Milani & Gronchi 2010).

2.7 Computing the magnitude of the heliocentric position

At this point we proceeded to perform the numerical estimation of the variables of interest $r, r ˙, ρ, ρ ˙$ . In principle, there is a geometric relationship between R, r, and ρ called the geometric equation (Danby 1962):

r 2 = R 2 + ρ 2 + 2 R ρ cos ε

(25)

Where $cos ε = R^⋅ ρ^$ . Up to this point, the constant C and cos ε are determined numerically (Fig. 1, Block 9) since the variables on which they depend are known quantities. From eq. (24), then:

ρ 2 = R 2 C 2 (1 − 2 R 3 r 3 + R 6 r 6)

(26)

By replacing the previous expression into (25) and multiplying it by C²r⁶, the following expression is obtained:

P (r) = C 2 r 8 − R 2 r 6 (C 2 + 2 C cos ε + 1) + 2 R 5 r 3 (1 + C cos ε) − R 8 = 0

(27)

The above expression is a polynomial equation of the 8^th degree in r. By solving it, the value of r is found (Fig. 1; Block 10).

2.8 Determination of State Vector, Orbital Elements and Ephemerides

In order to find a preliminary orbit and subsequently propagate ephemerides, the following Matlab functions were implemented:

• Solutions for r that were either imaginary or negative were filtered, as well as the trivial solution r = R (Milani et al. 2008; Fig. 1, Block 11).
• Eq. (25) for ρ with each filtered value of r was solved (Fig. 1, Block 12). Then, the invalid solutions for ρ were filtered (Fig. 1, Block 13).
• By using the eq. (22), the corresponding value for radial velocity was obtained $ρ ˙$ (Fig. 1, Block 14).
• Using the already-known magnitudes, the state vector (3) was determined (Fig. 1, Block 15).
• The orbit to generate ephemerides using the f and g series was propagated (Danby 1962; Fig. 1, Block 16).
• The correction for aberration was applied (Fig. 1, Blocks 16 to 18); then, the state vector was converted to orbital elements.
• Finally, the orbital elements and the ephemerides of the minor body were obtained (Fig. 1, Block 19).

2.9 Analysis of Errors

One way to carry out the error analysis is to compare all the estimated orbital parameters with the nominal ones; however, this is quite difficult (Schaeperkoetter 2011). An alternative is to reduce the number of parameters to be compared, considering that in any orbit the orbital parameters can be grouped into two groups, some associated with shape and others associated with orientation. The first contains information regarding the orbit shape on orbit plane: the semi major axis and eccentricity (a, e), while the second group contains information in respect to the relative orbit orientation: inclination, longitude of ascending node, and argument of perigee (i, Ω, ω). These error parameters are referred to as error in shape d, and orbit orientation Φ, respectively. This technique consists in reducing the number of parameters to be compared from 5 to 2 (Mortari et al. 2006). This technique has the advantage of making the graphical interpretation of the error easier, using a polar representation. In our case, the latter method is useful because we are using several sample asteroids, and with this analysis, it is possible to get a more global idea of the results of the method.

If the nominal parameters are (a, e, i, Ω, ω, θ) and the estimates are (a^* , e^* , i^*, Ω^* , ω^*, θ^*) , where θ is true anomaly, the error in the shape d is calculated as:

d = (a − a *) 2 + (b − b *) 2

(28)

Where $b = a 1 − e 2$ is the minor semi-axis. Orbit shape is related with the major and minor semi-axis which are dimensionally consistent parameters. Using both parameters the orbit shape can be represented as a point in the a − b plane. Therefore, the orbit error shape can be simply described by the eq. (28).

For orbit orientation, error Φ is calculated as:

cos Φ = 12 (t r [C C * T] − 1)

(29)

Where

C = R 3 (ω + θ) R 1 (i) R 3 (Ω) = [r^h^× r^h^] T

(30)

Being R₁ and R₃ the rotation matrices around the first and third coordinate axis, respectively. Mathematically, angle Φ is the main angle of corrective matrix between matrices CC and C^*. This can be interpreted as the angle between the directions of the estimated angular momentum and the real one; if this angle is small, the estimated orbit resembles the real one in terms of its position and orientation in three-dimensional space.

In the description of an orbit error, there are two parts: an error in the orientation Φ, which is an angle, and another in the position d, which is a distance. Hence, a polar representation is used to describe the error of the orbit through the point (Mortari et al. 2006):

E = d e / Φ

(31)

In this representation, the error will be smaller, the closer the point is to the origin of coordinates, and smaller the angle of inclination for the positive x-axis.

3. RESULTS

The developed algorithms were implemented as Matlab functions. The set of asteroids listed in Table 1 was used to validate the proposed methodology. As input data, observations reported to MPC (https://www.minorplanetcenter. net/db_search) and by OAUTP (MPC code W63) were used. Because of in the OAUTP we carry out observation programs in minor bodies, we decided to test our methodology with both NEA and MBA asteroids. From these asteroids, we had already made observation reports, and we complemented with those recorded by other observatories. These observations cover the observation intervals shown in the second column of Table 1 (in all cases, the observational interval used is a VSA). In the web site (https://www.utp. edu.co/observatorioastronomico/astrometria/orbital-elements- and-recovery-using-laplace), full data tables of the observations used in this study are available.

Table 1. Samples of the asteroid recovery. The number of input data N, interval of the initial observations Δt, the orbit type, the proper motion η, and the ρ value are shown.

Asteroid	N	VSA (Δt)	Type	η (°/day)	Real Pos. ρ (au)
(1864) Daedalus	16	22d 3h 25m	NEA/Apollo	0.3147	2.2636
2003 GW	13	18d 3h 40m	NEA/Apollo	0.7663	0.8677
(4690) Strasbourg	19	7d 4h 28m	Hungaria	0.2986	1.3899
2019 JA8	25	19d 1h 20m	NEA/Amor	0.3836	0.3255

(1738) Oosterhoff	33	17d 16h 00m	MBA	0.3107	1.0874
(2717) Tellervo	23	16d 2h 56m	MBA	0.2106	1.6472
(1568) Aisleen	16	20d 7h 46m	MBA	0.2825	1.5659
(2235) Vittore	24	11d 22h 34m	MBA	0.0778	3.0932

Download Excel Table

The Poincaré interpolation and the calculation of the attributable vector were performed to apply the modification of the geocentric Laplace's method. This process resulted in a state vector that was used to determine orbital elements of each of the studied asteroids. The results are shown in Table 2.

Table 2. Orbital elements: Semimajor axis (a), eccentricity (e), inclination (i), the argument of perihelion (Ω), ascending node (ω), time of perihelion passage (T₀) obtained for this study (TS) compared with the nominal ones taken from NASA JPL Web-interface service (JPL) at time of reference t_ref

Asteroid	t_ref(JD)	Data	Orbital elements
			a (AU)	e	i (°)	Ω (°)	ω (°)	T₀ (JD)
			(1864) Daedalus	2458789.80310	TS	1.4639	0.6098	22.7320	7.2799	325.2213	2458603.39671
		JPL	1.4610	0.6144	22.2092	6.6280	325.6275	2458604.12044
2003 GW	2458354.55596	TS	1.8647	0.4848	48.3890	183.4034	91.8637	2458254.98649
		JPL	1.8207	0.4762	49.4358	183.2111	90.6109	2458253.92435
(4690) Strasbourg	2458188.03505	TS	1.9536	0.0862	17.1201	298.1088	115.1864	2458016.23371
		JPL	1.9374	0.1089	16.9095	295.7938	105.4774	2457993.92200
2019 JA8	2458627.44160	TS	2.6154	0.5296	10.1768	74.7833	202.4851	2458580.45560
		JPL	2.4197	0.4965	9.5019	79.2309	197.7623	2458673.81805
(1738) Oosterhoff	2458032.92310	TS	2.1628	0.1945	5.5060	37.9928	294.1069	2458019.14392
		JPL	2.1835	0.2025	4.8774	44.1111	284.4315	2458011.86828
(2717) Tellervo	2458184.20493	TS	2.2555	0.2810	2.7606	162.0936	159.6214	2457782.89620
		JPL	2.2146	0.2185	3.2854	164.8653	163.5006	2458627.03995
(1568) Aisleen	2457434.87988	TS	2.3667	0.2735	24.9534	144.2715	227.5491	2457182.98599
		JPL	2.3517	0.2541	24.8966	146.2405	228.7325	2457187.56159
(2235) Vittore	2458675.39060	TS	3.2352	0.2160	18.0316	206.3595	269.6413	2457857.97201
		JPL	3.2043	0.2149	18.7807	205.0291	274.4220	2459510.61840

Download Excel Table

Otherwise, Fig. 3 shows the orbits in the heliocentric ecliptic system, as well as its projections on the axes of the NEA asteroids and Hungarian-type asteroid. Fig. 4 shows the same for MBA-type asteroids. The animations of the trajectories obtained in this study are available at https:// www.utp.edu.co/observatorioastronomico/astrometria/ orbital-elements-and-recovery-using-laplace.

Fig. 3. Orbits of the NEA and Hungaria-type asteroids. Plots are in a heliocentric ecliptic system.

Download Original Figure

Fig. 4. Orbits of the MBA-type asteroids. Plots are in a heliocentric ecliptic system.

Download Original Figure

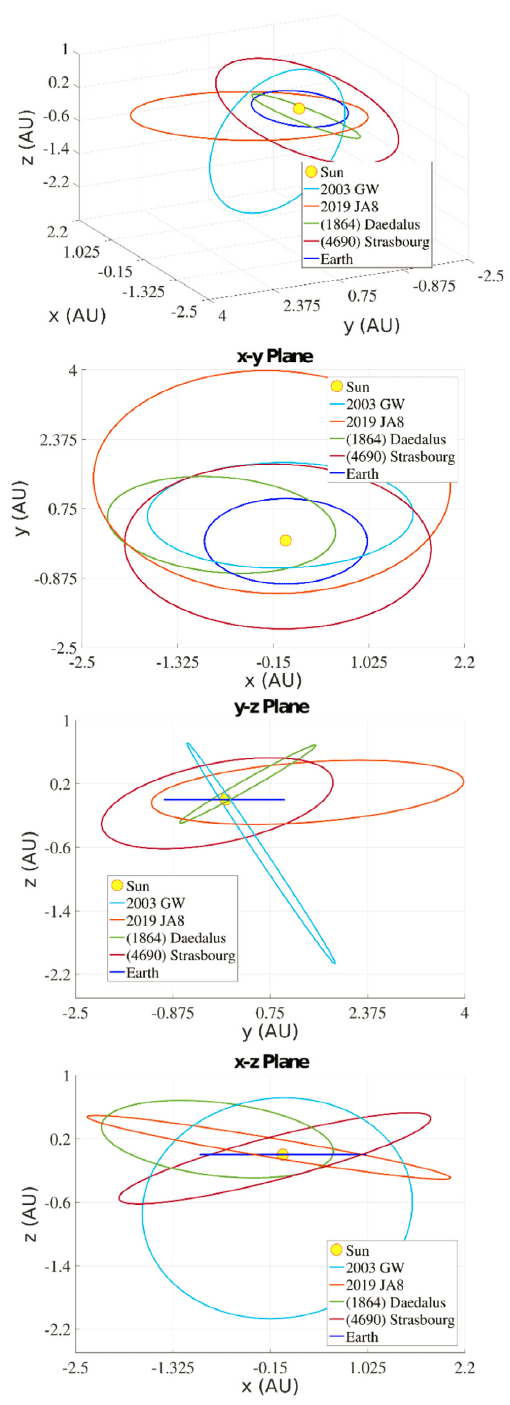
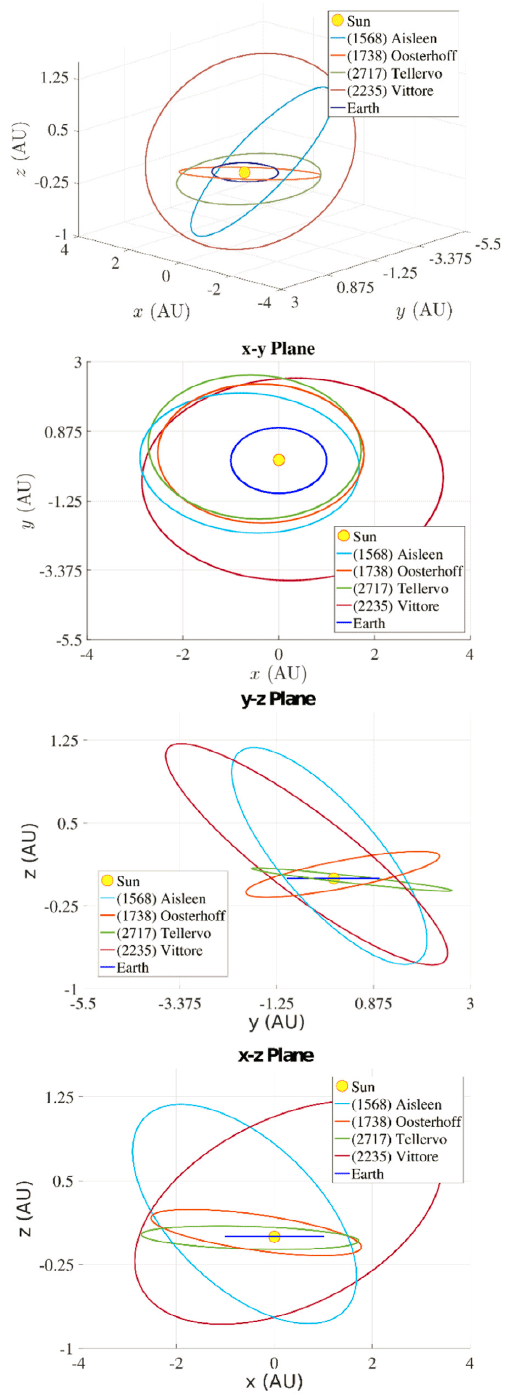
To analyze the obtained results, the errors in shape and orientation of the orbits for the set of 8 asteroids were estimated. The orbital elements data taken from the NASA JPL Web-interface service (https://ssd.jpl.nasa.gov/horizons. cgi#results) were assumed to be true. The results are shown graphically in Fig. 5.

Fig. 5. Estimated orbital errors for each asteroid: (a) The error in shape, and (b) the error in orientation.

Download Original Figure

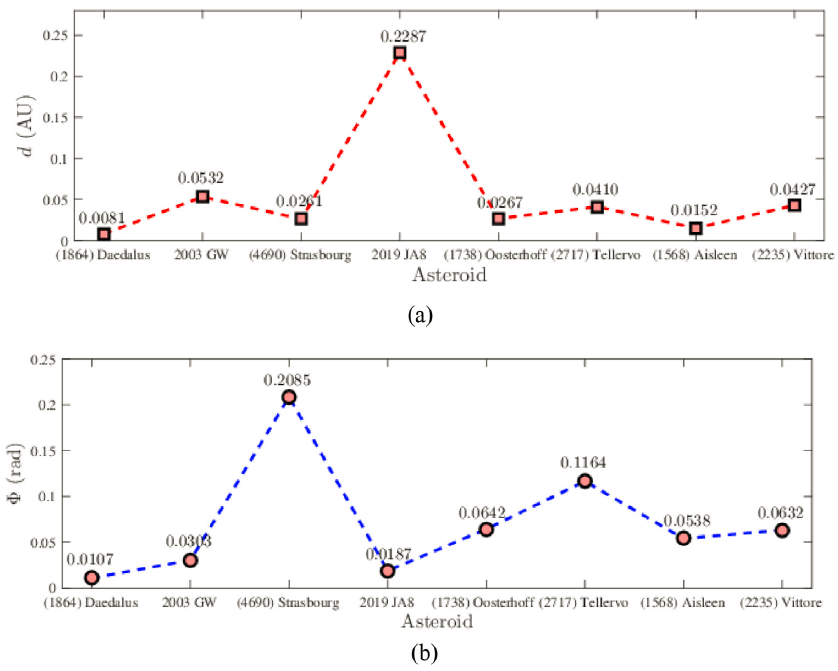
As can be seen, the errors in shape are less than 53 × 10^–3 AU, except for the 2019 JA8 asteroid (Fig. 5a). These results are comparable with the real model of the orbits, which is intrinsically linked to the use of a two-body model (Gronchi et al. 2010). The error orientation Φ is less than 0.1 rad, except for the (4690) Strasbourg (Fig. 5b).

The errors in each of the estimated orbits in a polar representation are shown in Fig. 6. It is observed that the orbits are of good quality even when the dynamic model used only considers two bodies. Fig. 6a illustrates the object that shows the highest estimated orbital error is 2019 JA8. This may be because this asteroid was at an average distance from the observer of less than 0.35 AU, with a significant proper motion (Table 1). Under such conditions, Laplace's method should consider the position of the observer on Earth (which implies the reformulation of the entire mathematical model). Additionally, due to the proximity of the asteroid to the Earth, the gravitational force influence of the planet should be considered when calculating. That is, a three-body model should be implemented. On the other hand, in thcase of (4690) Strasbourg, the orientation error was greater than the other asteroids. This may be because this one was tested with a shorter time interval. However, as we clarified in section 2.9, seeing the error in a polar representation is important. Despite the aforementioned challenges, the estimated orbit for both 2019 JA8 and (4690) Strasbourg are of enough quality to recover this object again.

Fig. 6. Orbit error complex representation for the asteroids. (a) All used asteroids, and (b) Zooming into the plot.

Download Original Figure

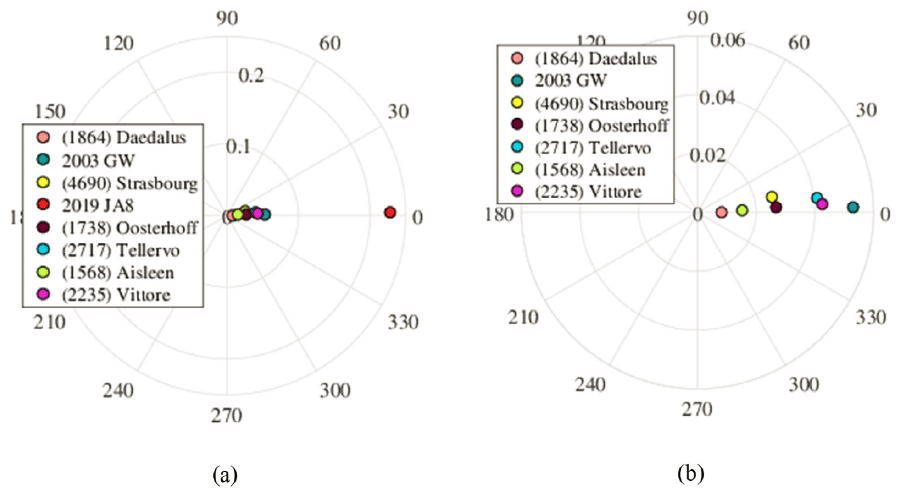
In the rest of the cases, when zooming into the plot (Fig. 6b), the errors get close enough to the origin, and with minimal angles (the latter also for 2019 JA8). In this way, it is observed that the estimated orbits were of good quality.

However, despite the proximity between the estimated orbital parameters in respect to the real ones, the effective utility for the IOD method is determined by the capacity it has to produce ephemerides with enough precision so that the body can be re observed after initial observations. The purpose of our algorithm is to establish an IOD with the available information of the object. The IOD allows for the establishment of an ephemeris to perform the recovery of that object. This recovery allows for the gathering of a great number of observations. The more observations, the better the estimation of the orbit, which is the least-squares principle procedure input (Danby 1962). In our case, we tested the recovery simulation, calculating the ephemeris for 15, 30, 45, and 60 days after the last observation for each of the asteroids presented in Table 3. As it is evident in Table 3, it was possible to recover all the objects. The results are compared to those provided in the NASA JPL Web-interface service. During this time, it would be possible to collect a significant amount of additional observations that would improve the IOD.

Table 3. Ephemerides for sample asteroids. Date shows time in UT for the ephemerides at 15, 30, 45 and 60 days after the last observation entered as input. The symbols α and δ refer to the coordinates in right ascension and declination, respectively.

Ephemerides
Date (UT)	a (h min s)	δ(^o ʹ ʺ)	Δa (arcmin)	Δδ (arcmin)
(1864) Daedalus
2019 11 29.1372	11 29 19.46	+24 03 50.6	1.63	1.87
2019 12 14.1372	11 39 42.23	+24 24 10.7	2.27	3.12
2019 12 29.1372	11 43 39.15	+25 34 09.7	2.40	4.56
2020 01 13.1372	11 39 13.40	+27 34 27.9	2.38	6.00
2003 GW
2018 09 19.3861	03 09 34.33	-10 53 17.3	4.80	7.79
2018 10 04.3861	02 51 16.90	-23 27 08.0	5.17	17.47
2018 10 19.3861	02 25 45.95	-32 20 50.9	0.84	26.34
2018 11 03.3861	02 00 56.36	-36 52 18.7	5.87	31.44
(4690) Strasbourg
2018 03 28.0838	06 37 27.64	+17 52 40.5	0.94	0.77
2018 04 12.0838	07 00 57.52	+16 12 08.3	3.65	2.00
2018 04 27.0838	07 26 41.13	+14 28 04.4	7.56	3.75
2018 05 12.0838	07 53 50.96	+12 34 22.5	12.78	6.04
2019 JA8
2019 06 18.1566	14 57 35.73	–16 02 15.6	4.77	6.41
2019 07 03.1566	15 14 59.64	–27 08 31.8	13.06	12.65
2019 07 18.1566	15 53 29.46	–37 30 02.9	28.06	14.11
2019 08 02.1566	16 52 45.23	–44 36 15.7	41.94	6.93
(1738) Oosterhoff
2017 10 29.1566	21 17 11.76	–21 27 46.9	2.51	0.06
2017 11 13.1566	21 43 17.56	–18 22 44.3	2.32	0.43
2017 11 28.1566	22 11 25.77	–15 00 19.6	1.11	1.33
2017 12 13.1566	22 40 45.36	–11 23 57.0	1.14	2.74
(2717) Tellervo
2018 03 28.2334	12 16 57.64	+00 12 15.5	0.36	0.14
2018 04 12.2334	12 02 47.46	+02 01 06.7	1.91	1.79
2018 04 27.2334	11 52 01.91	+03 21 53.1	6.84	4.80
2018 05 12.2334	11 46 49.88	+04 01 15.8	13.37	8.52
(1568) Aisleen
2016 03 13.3917	06 24 28.28	+09 36 12.1	5.35	1.32
2016 03 28.3917	06 38 35.71	+12 19 33.9	10.13	2.11
2016 04 12.3917	06 56 15.66	+14 22 50.3	15.59	2.53
2016 04 27.3917	07 16 28.30	+15 49 38.4	21.69	2.39
(2235) Vittore
2019 07 31.1324	21 58 00.58	+10 00 38.6	0.19	0.17
2019 08 15.1324	21 48 36.92	+09 13 54.7	0.68	0.10
2019 08 30.1324	21 38 40.39	+07 53 32.2	1.45	0.06
2019 09 14.1324	21 30 03.36	+06 10 31.5	2.39	0.43

Download Excel Table

To simulate a possible recovery of each of the objects, the error in right ascension α and declination δ, were calculated as $(Δ α, Δ δ) = | α v − α a, δ v − δ a |$ .

Where (α_v, δ_v) are the NASA JPL coordinates and (α_a, δ_a) are obtained in this study by propagating the state vector obtained by using modification of the geocentric Laplace's method to the dates indicated in Table 3.

Columns 4 and 5 of Table 3 show the errors calculated for each of the coordinates. For example, the highest error is recorded at 41.94 arcmin in right ascension, for the 2019 JA8 asteroid, during a period of two months after its last observation used as input. As can be seen, the highest recorded error in decline was 2003 GW with 31.44 arcmin. At the mean time of the observations, both asteroids were at a very close distance to Earth (as can be seen in Table 1) and therefore their mean motion are greater than the others. This explains the reason why major errors occurred. In both cases, the obtained values make the re-observation very likely for these dates, while considering the estimation of the initial state vector was made from a geocentric approach.

The boundary conditions for the modification of the geocentric Laplace's method are determined by the convergence of the method. In this case, the convergence is subject to the fact that it is a VSA; therefore, it would not be possible to apply it to data that have too short observation intervals (TSA, too short arcs). In this case, it would be necessary resort to other methods developed by Mosquera & Salazar (2019). Geocentric Laplace's method would not be optimal for objects that get too close to Earth at the time of their observation (NEAs at their closest approach); moreover, it would not be suitable for studying objects that are at very large distances (that present a very low proper motion) as in the case of observing trans Neptunian objects.

Likewise, the Figs. 7 and 8 show the ephemerides obtained from the NASA JPL (purple dots) compared to those estimated in this study (pink squares). The field of vision given by the instrumental assembly of the OAUTP is 95´ × 72´ (blue dotted-line box).

Fig. 7. Calculated ephemerides for dates after the last recorded input for NEA and Hungaria-type asteroids: from row one, the results are shown for: (1864) Daedalus, 2003 GW (4690) Strasbourg and 2019 JA8, respectively. Blue dotted-line box is the field of vision given by the instrumental assembly of the OAUTP.

Download Original Figure

Fig. 8. Calculated ephemerides for dates after the last recorded input for MBA-type asteroids: from row one, the results are shown for: (1738) Oosterhoff (2717) Tellervo (1568) Aisleen y (2235) Vittore, respectively. Blue dotted-line box is the field of vision given by the instrumental assembly of the OAUTP.

Download Original Figure

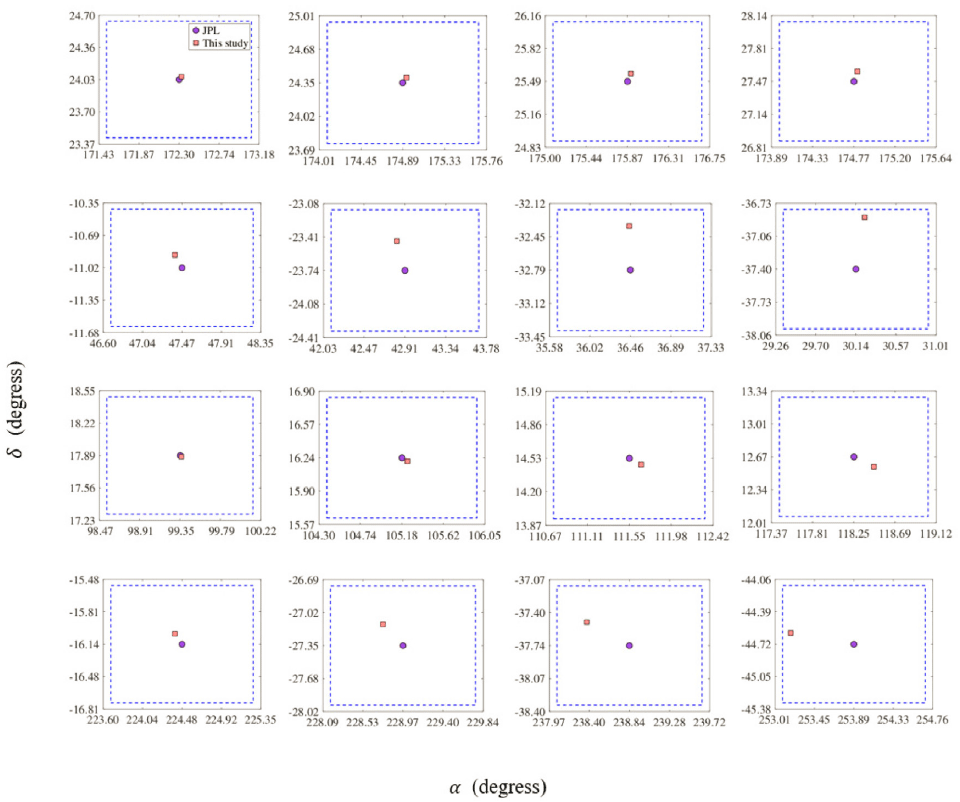
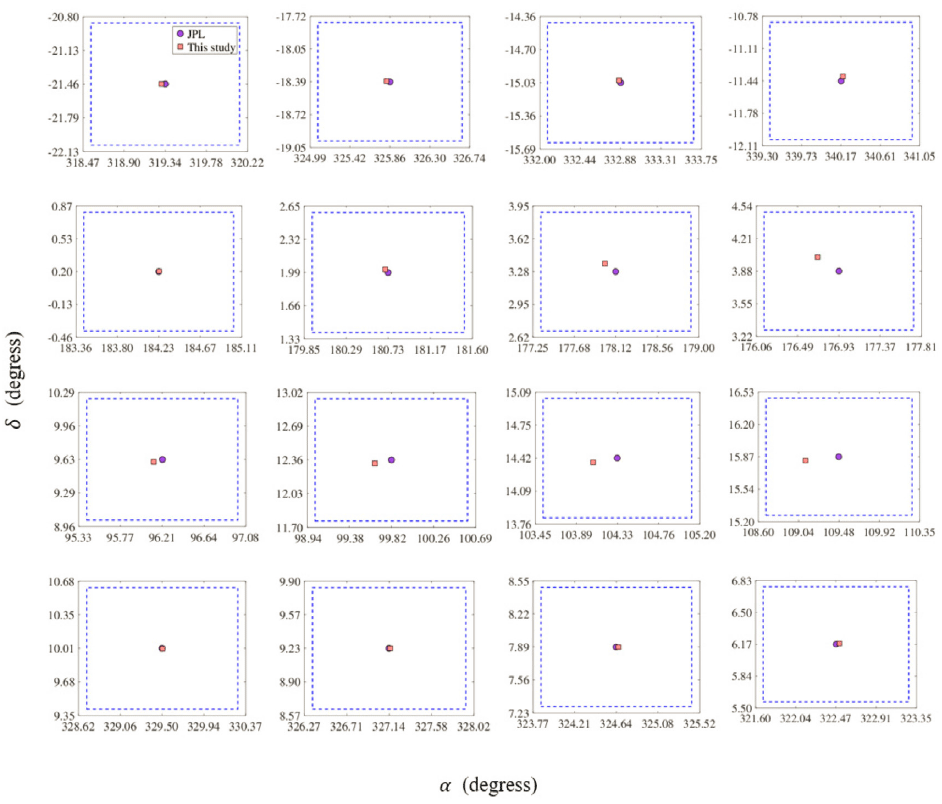
According to Figs. 7 and 8, all the studied asteroids would be recoverable from the OAUTP within the field of observation, making the recovery procedure possible as well as a subsequent refinement of the initial calculation of the orbit. The most significant error between the calculated ephemerides and the actual position was for 2019 JA8 asteroid. This result was expected, given the error in the polar representation (Fig. (a)). However, despite this, the object can still be recovered within the visual field.

4. CONCLUSIONS

It was demonstrated that the modification of the geocentric Laplace's method, which considers an input given by a set of astrometric measurements of a minor body (generally more than three observations), permitted the estimation of values for quantities such as proper motion and geodesic curvature; with which the algorithm's equations were solved. From the data used, the one that covers the longest time interval is approximately 22 days. It was possible to verify that, despite the short time intervals, the methodology allows for the production of initial orbits of enough quality to subsequently re-observe the bodies.

The errors of the estimated orbit concerning those provided by the HORIZONS Web-Interface service of NASA's JPL were estimated. These errors were grouped in shape and orientation for each of the orbits so that the errors in shape were less than 53 × 10^–3 AU, except for the asteroid 2019 JA8, and in terms of orientation, the errors were less than 0.1 rad, except for (4690) Strasbourg. Both sets of errors are expected values when using the two-body problem as a dynamic model, i.e. orbital shape and orientation are expected values for Keplerian type orbital parameter.

Additionally, the ephemeris for each of the bodies studied, up to two months after the last observation used as input, was estimated. These results were compared with the NASA JPL Web-interface service. In all cases, it is shown that they are recoverable within the field of vision of the instrumentation of the OAUTP (95´ × 72´). The highest error obtained in α was 41.94´ and 31.44´ for δ, respectively for (2019 JA8) and (2003 GW) asteroids. Therefore, the proposed methodology shows the importance of modification of the geocentric Laplace's method . The method is relatively simple to implement, and the results allow for the recovery of minor bodies from the Solar System, even when the input data observations represent very short arcs.

This study represents the second step in the minor bodies observation program of the Solar System implemented in the Astronomical Observatory of the Technological University of Pereira, after obtaining the MPC code (W63). The codes written in Matlab (https://www.utp.edu.co/observatorioastronomico/ astrometria/orbital-elements-and-recovery-using-laplace) can be useful for observatories that begin their process of studying the IOD of asteroids.

ACKNOWLEDGMENTS

The authors express their gratitude to the Technological University of Pereira for their financial support for the execution of the research project “Methodology for the Generation of Ephemeris and the Refining of the Orbit of Small Bodies of the Solar System of Recent Discovery”, code 3-18-9.

References

Aristova EY, Aushev AA, Baranov VK, Belov IA, Bel'kov SA, et al., Laser simulations of the destructive impact of nuclear explosions on hazardous asteroids, J. Exp. Theor. Phys. 126, 132-145 (2018).

Bowell E, A new protocol for the operation of the minor planet center, in AAS/Division for Planetary Sciences Meeting, Sep 1999.

Curtis HD, Orbital Mechanics for Engineering Students: Aerospace Engineering (Elsevier Science, San Diego, CA, 2014).

Danby J, Fundamentals of Celestial Mechanics (Macmillan, New York, NY, 1962).

Gauss C, Theoria motus corporum coelestium in sectionibus conicis solem ambientium (Sumtibus F. Perthes et I. H. Besser, Hamburg, 1809).

Gauss KF, Davis CH, Theory of the Motion of the Heavenly Bodies Moving about the Sun in Conic Sections (Dover Publications, New York, NY, 2004).

Gronchi GF, Classical and modern orbit determination for asteroids, Proceedings of the International Astronomical Union, 2004 (IAUC196), 293-303 2004.

Gronchi GF, Dimare L, Milani A, Orbit determination with the two-body integrals, Celest. Mech. Dyn. Astr. 107, 299-318 (2010).

Hwang O, Jo JH, Trends of initial orbit determination accuracy for time interval change between three pairs of measurement datas, J. Astron. Space Sci. 26, 529-546 (2009).

10.

Klokacheva MY, Determination of a preliminary orbit by the laplace method, Sov. Astron. 35, 428 (1991).

11.

Marsden B, Initial orbit determination-the pragmatist's point of view, Astron. J. 90, 1541-1547 (1985).

12.

Milani A, Gronchi G, Theory of Orbit Determination (Cambridge University Press, Cambridge, UK, 2010).

13.

Milani A, Gronchi GF, Farnocchia D, Knežević Z, Jedicke R, et al., Topocentric orbit determination: algorithms for the next generation surveys, Icarus. 195, 474-492 (2008).

14.

Milani A, Gronchi GF, Knežević Z, New definition of discovery for solar system objects, Earth Moon Planets. 100, 83-116 (2007).

15.

Milani A, Gronchi GF, Knežević Z, Sansaturio ME, Arratia O, Orbit determination with very short arcs: II. identifications, Icarus. 179, 350-374 (2005).

16.

Milani A, Gronchi GF, Vitturi MDM, Knežević Z, Orbit determination with very short arcs. I admissible regions, Celest. Mech. Dyn. Astr. 90, 57-85 (2004).

17.

Milani A, Sansaturio ME, Chesley SR, The asteroid identification problem IV: attributions, Icarus. 151, 150-159 (2001).

18.

Mirtorabi T, A simple procedure to extend the gauss method of determining orbital parameters from three to n points, Astrophys. Space Sci. 349, 137-141 (2014).

19.

Mortari D, Scuro SR, Bruccoleri C, Attitude and orbit error in n-dimensional spaces, J. Astron. Sci. 54, 467-484 (2006).

20.

Mosquera DE, Salazar EAQ, Determination of the admissible region of asteroids with data from one night of observation, J. Phys. Ser. 1247, 012038 (2019).

21.

Poincaré H, Mémoires et observations. sur la détermination des orbites par la méthode de laplace, Bull. Astron. Serie I. 23, 161-187 (1906).

22.

Quijano A, Rojas M, Chaves L, Cálculo de los parámetros orbitales del asteroide 2003QO104, Rev. Colomb. Fís. 42, 4 (2010).

23.

Schaeperkoetter AV, A comprehensive comparison between angles-only initial orbit determination techniques, PhD Dissertation, Texas A&M University (2011).

24.

Sokolskaya MJ, On the laplacian orbit determination of asteroids, Planet. Space Sci. 45, 1575-1580 (1997).

25.

Vallado D, McClain W, Fundamentals of Astrodynamics and Applications (Microcosm Press, Dordrecht, The Netherlands, 2001).

26.

Villarraga SJ, Quintero-Salazar EA, Corrección topocéntrica de parámetros orbitales obtenidos mediante las integrales de Kepler para asteroides MBA y NEO, Rev. Acad. Colomb. Cienc. Ex. Fís. Nat. 40, 43-52 (2016).

27.

Villarraga SJ, Salazar EAQ, Galvis JAA, Acquisition of the minor planet center code for the astronomical observatory of the technological university of Pereira (w63), Tecciencia. 12, 43-50 (2017).