Determination of Geostationary Orbits (GEO) Satellite Orbits Using Optical Wide-Field Patrol Network (OWL-Net) Data

Although sequential estimation is better suited to realtime monitoring compared to a batch-type estimator, the batch-type estimator is more accurate and robust (Crassidis & Junkins 2011). Considering the objective of this study, to obtain accurate orbit solution for long-time prediction, and the process of the optical tracking system where the measurement data is extracted from optical images after observations, the batch least squares method was employed in this work. The batch least squares is the simplest method of estimating epoch states using a set of observed data over a period. Fig. 1 shows a flowchart of the batch least squares filter process, and the notation used in the figure is equivalent to the following description.

A batch filter algorithm estimates a value that can be used to minimize a residual between a value predicted by a system model (F) and a practical observation data set (Y) which consists of N data points, as shown in Eq. (1).

On the right side, X is the solve-for vector, Z is the considered vector, and ϵ is the observation error. The solvefor vector has a specific uncertainty, reflected in the form of the covariance matrix. This estimation method can be described as an optimization problem used to find a solution that can minimize an objective function (Q), as shown in Eq. (2) (Schutz et al. 2004).

where W is a weight matrix that consists of the inverse of the variance of each observation, and X₀ and ${\text{P}}_{{\text{ΔX}}_{\text{0}}}$ are the a priori solve-for vector and covariance matrix, respectively.

Under the assumption that the solve-for vector of the i^th iteration (${\widehat{X}}_i$) is sufficiently close to the optimal solution (X), the above system and objective function can be linearized based on a Taylor series, and the solve-for vector is then updated by solving a normal equation as Eq. (3). Note that the considered vector is excluded from the linearization process as it is not an estimation target (Long et al. 1989).

where ΔY_i is the measurement residual of the i^th iteration derived as Eq. (4).

H is the Jacobian matrix, a partial differential equation of the system model with respect to the solve-for vector. In the OD problem, the system model is composed of a dynamics model and an observation model, and the Jacobian matrix can be expressed by the multiplication of a state transition matrix (Φ) and a sensitivity matrix (A) based on the chain rule (Long et al. 1989).

This iterative process is repeated until the cost reduction ratio is smaller than the criteria (ε), as in Eq. (6).

A covariance matrix which indicates the accuracy of the estimation result is shown in Eq. (7).

In this study, the batch estimator was developed in the Matlab environment employing the General Mission Analysis Tool (GMAT) as the dynamics model. GMAT was developed and released for public use by NASA, and the force models and numerical integrator in the software have been verified and applied to practical mission analysis (Hughes et al. 2014).

A covariance matrix calculated through a batch filter indicates the accuracy of the derived estimation results based on a system model and the observation quality. The statistical validity of the algorithm can be verified by confirming the consistency between the covariance matrix and practical OD estimation results from a Monte Carlo simulation. The Monte Carlo simulation was conducted 1,000 times using a priori state error corresponding to the a priori covariance and pseudo-observations with Gaussian errors reflecting observation noise. The verification was conducted for GEO, similar to previous research where the same process was used for LEO (Lee et al. 2017). The details of the simulation environment used to verify the batch filter are described in Table 1. The reference orbit was defined in the form of Keplerian orbit elements, and the force model was set as two-body motion for simplicity. A single observatory located in Daedeok was employed, and several properties were specified for generating pseudo-observations: path length is the total time-span required to take optical images, exposure time is the time-span of an image, exposure period is the period between successive images, data frequency is the frequency used to extract data points from the image, and noise is a standard deviation of white noise. Fig. 2 shows a comparison of the estimation errors of the Monte Carlo simulation and covariance ellipsoid. The results of the Monte Carlo simulation show that 99% of the OD estimation results fall within a 3σ error range estimated by the covariance ellipsoid. This verifies that the estimation is statistically reliable and that the covariance matrix can be used to analyze the accuracy of the results.

In this section, the effect of the arc length, i.e., the time of a path of the observation, on the OD accuracy is analyzed. In general, the arc length of an object in GEO is about hours while that of an object in LEO is about 5 minutes. In the numerical simulation, the arc length was gradually increased to 72,000 seconds (20 hours), while the other conditions such as the observation interval were maintained at constant values. Fig. 3 shows a comparison of the position and velocity errors according to the arc length when the level of noise was 1 and 100 arcseconds. For the observation data with 100 arcseconds of noise, for instance, the position errors were 89 km when the arc length was 7,200 seconds (2 hours) and 0.5 km when the arc length was 72,000 seconds (20 hours). This shows that the accuracy of the OD with low-quality (high-level noise) observation data improves significantly as the arc length increases.

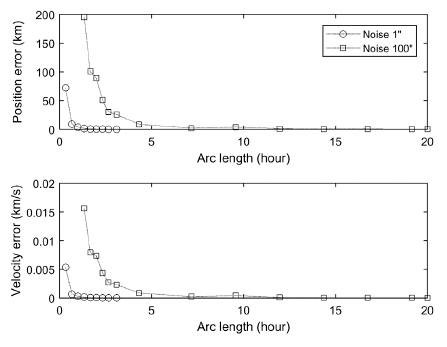
The detailed trends of the accuracy of the estimation according to the arc length with a realistic noise level, under 20 arcseconds, are described in Fig. 4. The result shows that the accuracy of the OD significantly improves as the arc length increases; when the arc length was 10 times longer, the accuracy of the position and velocity improved by a factor of 100 or higher. For example, the position error was 5 km when the level of noise was 5 arc-seconds and the arc length was 7,200 seconds, and that error became 20 m when the level of noise was same but arc length was increased to 72,000 seconds.

This improvement can be mathematically explained by the number of observation data points. It is clear that the first term in Eq. (7) can be expressed as the summation of each Jacobian if the weight matrix is diagonal, i.e., each observation data point is independent, as shown in Eq. (8). Since the entry of the term is applied to an inverse of the covariance, increasing the number of observation data points improves the accuracy.

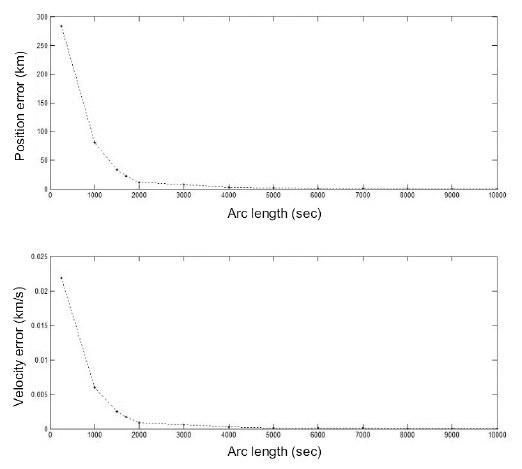
The accuracy of the OD was examined under conditions with a consistent number of observation data points and an increasing arc length from 250 to 10,000 seconds. Contrary to the previous analysis, the number of observation data points was maintained in the range of 1,700–1,790 by adjusting the observation interval as the arc length was varied. Using a consistent number of observations, the position errors were on the order of hundreds of kilometers and hundreds of meters for arc lengths of 250 and 10,000 seconds, respectively, and the velocity errors were 2.18 and 0.04 m/s for these are lengths (Fig. 5). This shows that the accuracy of OD tends to improve with increase in the observation arc length, which occurs because more dynamical information about the orbit is provided by a longer time of observation.

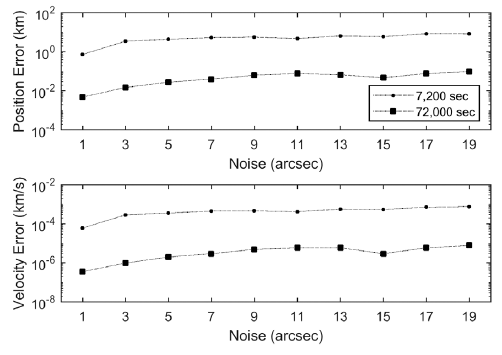
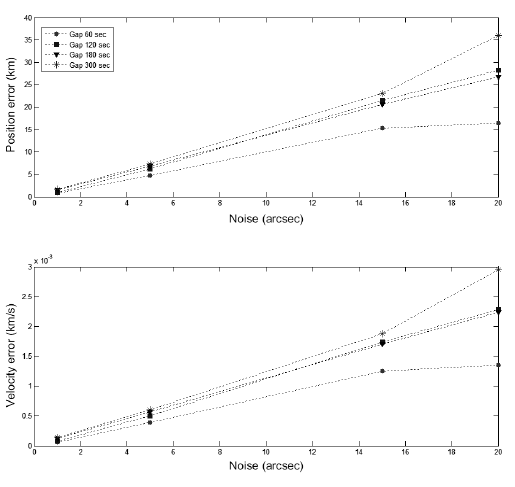
The accuracy of the OD for the GEO satellite was analyzed using various observation intervals, with the condition of a fixed arc length of 7,200 seconds and a noise level varying from 1 to 20 arcseconds. The accuracy of the OD tends to increase as the observation interval is shortened (Fig. 6). As shown in Fig. 6, the sensitivity to the interval increases as the level of noise increases: the difference between the position errors at the observational intervals of 60 and 300 seconds were 2.1 km and 19 km when the noise levels were 5 and 20 arcseconds, respectively.

It was found that the observation interval does not significantly affect the OD accuracy, especially with highquality (low-level noise) observation data. Compared to the results presented in Section 3.1, the arc length is more significant than the observation interval, which indicates that it is more effective for precise OD to adjust the arc length, not the observation interval.

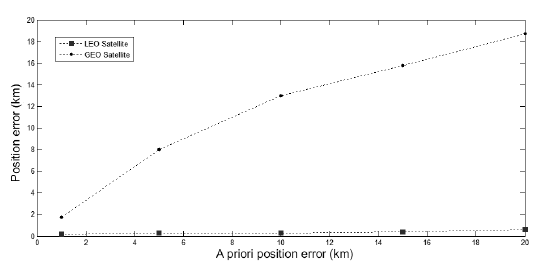
The a priori value of the solve-for vector is not clearly identified and has a specific uncertainty reflected in the form of an a priori covariance matrix. In this section, the effects of the a priori uncertainty on the accuracy of the OD are analyzed for the LEO and GEO cases. Fig. 7 shows the positional accuracy of the OD with respect to the a priori position uncertainty for LEO and GEO satellites with a noise level of 20 arcseconds. It indicates that the positional accuracy for LEO is within 200 m regardless of the a priori uncertainty, while that of the GEO satellite tends to increase as the a priori uncertainty increases. This result can be mathematically interpreted using the sensitivity matrix, which represents the relation between the solvefor vector and the observation. A large value of the matrix indicates that the solve-for vector can significantly change the measurement data. In the case of the angles-only measurement, the sensitivity matrix of a GEO satellite with a high altitude has small values while that of an LEO satellite is large, and it is geometrically comprehensible. This can be also explained mathematically. According to the definition of the final covariance (Eq. 6), the smaller sensitivity matrix exerts less influence on the final covariance and the effect of the a priori covariance is relatively large. Practically, the a priori covariance has more of an effect on the estimation precision in the GEO case than the LEO.

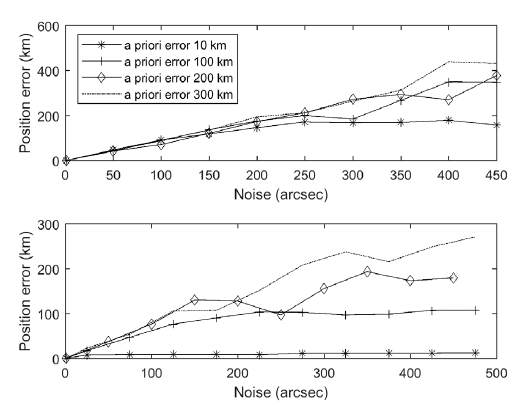
To verify this mathematical analysis, the OD results for the GEO satellite are compared using two cases: case 1 excludes the a priori covariance from the objective function and the normal equation, while case 2 employs the original components (Eq. 2, Eq. 3). The OD was carried out under the conditions of a priori uncertainty varying from 10 km to 300 km for the position, 0.01 km/s to 0.3 km/s for the velocity, and a level of noise from 1 to 500 arcseconds. The upper and lower figures in Fig. 8 show the positional accuracy of case 1 and case 2, respectively. In both cases, the effect of the a priori covariance matrix is insignificant with the low noise level. With the high noise level, however, the OD error is always within the a priori uncertainty in case 2, while in case 1, it increases without limit and proportionally to the level of noise, regardless of the a priori error. This indicates that the a priori covariance matrix prevents divergence or significant error compared to the measurement error.

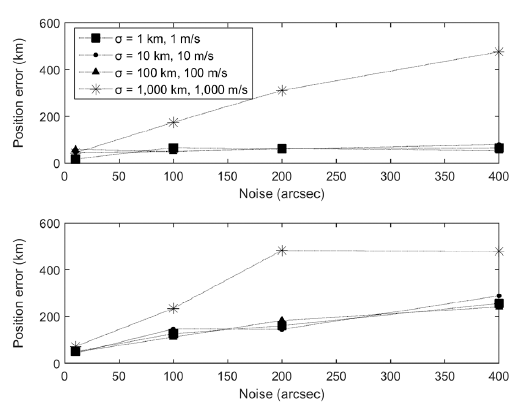
Each effect of the a priori covariance and a priori error was separately analyzed using another two cases: case 3 employs a fixed a priori error and varying a priori covariance, and case 4 takes a fixed a priori covariance and changing a priori error. Each case is divided into two subcases based on position and velocity. Case 3-1 includes fixed a priori error of 50 km and 0.05 km/s, while case 3-2 includes fixed a priori errors of 150 km and 0.15 km/s. A fixed a priori covariance matrix of 100 km and 0.1 km/s was used for case 4-1, and 150 km and 0.15 km/s for case 4-2. Note that the noise level was set from 10 to 400 arcseconds for all cases to check the trends, even though it is much larger than the actual value.

Fig. 9 exhibits the position error of case 3, which is within tens of kilometers with the covariance of under 100 km, even though the noise increases. A position error of larger than hundreds of kilometers was found when the covariance matrix implied 1,000 km in both sub-cases, and the dependence on the noise increased as the a priori error was increased. Fig. 10 presents the positional accuracy of case 4. It shows that the accuracy is independent of the a priori error when the noise level is 10 arcseconds, i.e., the OD is robust to a priori error with high-quality measurement data. Furthermore, the OD error is within the a priori covariance ellipsoid centered at the a priori error in all sub-cases. This verifies that the a priori covariance matrix prevents a significant scatter of the estimated states from the a priori states. In other words, the estimation accuracy is determined by the noise level if the a priori covariance covers the actual error. If not, the estimated states would be near the a priori states and the accuracy is depressed.

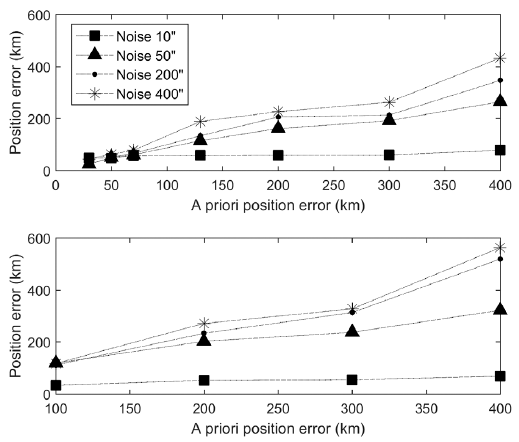
Through these analyses, it is confirmed that the a priori covariance is significant in the OD for GEO, especially when the measurement quality is poor. Therefore, an appropriate a priori covariance matrix based on the actual reliability of the a priori state vector must be applied to obtain more accurate OD results. The robustness of the OD with respect to the a priori error is also proved, i.e., the orbit solution can be obtained with an uncertain a priori state with a position error of 400 km.

In this section, Monte Carlo simulation with varying noise levels was carried out to analyze the effects of observation noise on the OD accuracy. Note that the noise was set from 1 to 100 arcseconds, unlike the actual value of several arcseconds, for characteristics analysis. Fig. 11 describes the changes in the accuracy of position and velocity according to the noise level, with fixed a priori errors of 10 km and 1 m/s in position and velocity. Just as in the analysis of an LEO satellite (Lee et al. 2017), the OD error in the GEO case also increases as the noise level of noise increases. The position error ranged from 0.4 to 30 km, and the velocity error reached from 0.1 to 1 m/s.

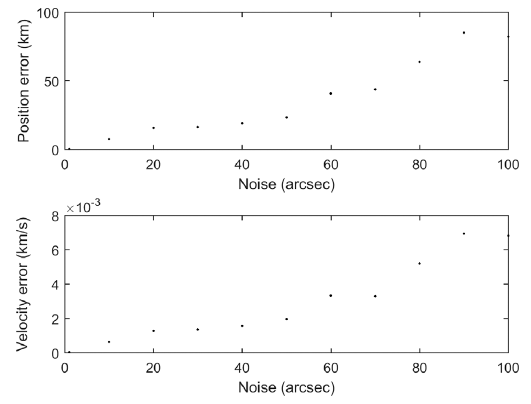
Geometrically, the angular distances corresponding to 5 and 100 arcseconds are 0.01 and 0.33 km at an altitude of 700 km (LEO) and 0.86 and 17.34 km at an altitude of 35,790 km (GEO), respectively. This analysis is consistent with the above results, where the accuracy of the OD decreases as the noise increases. The magnitude of the error in Fig. 11, however, is larger than the geometric analysis because the analysis only considers the projected position error without the line-of-sight error.

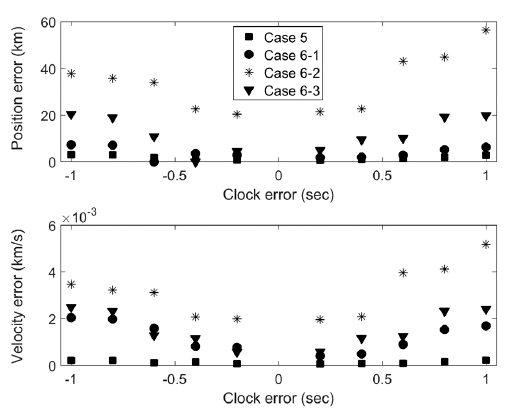
When extracting data from OWL-Net, two processes are performed: one process synchronizes the observation data and time, and the other combines the time log from the time server and extracted observation data (Park et al. 2018). Clock errors can occur in the second process, and the OD accuracy for GEO was analyzed by considering two cases: case 5 deals with a clock offset, i.e., an identical clock error is applied to the entire set of observation data, while case 6 handles a clock mismatch, i.e., a clock error is partially applied to the observation data. Case 6 is divided into subcases 6-1, 6-2, and 6-3, corresponding to clock mismatches on 25%, 50%, and 75% of the total observation data in each case. The level of observation noise was fixed as 15 arcseconds, and each case was repeated 100 times to obtain statistical results.

Fig. 12 shows the results of GEO OD according to the clock error. In case 5, the position error was about 3 km, which corresponds to the orbital motion of the GEO satellite, 3 km/s. On the other hand, in case 6, the accuracy was worse than that in case 5 because the clock mismatch serves as a non-linear error in the observation data which considerably degrades the OD accuracy. These results indicate that clock mismatch can cause significant estimation error, so such errors should be corrected for accurate OD results.

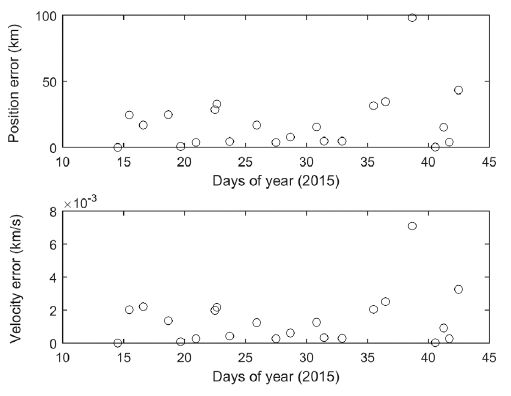
Since TLE is employed as the reference orbit, the accuracy of TLE was evaluated by an overlap analysis, prior to the OD. For the overlap analysis, successive TLEs are propagated for a certain time to generate an overlap period, and the difference between two trajectories are compared for that period. The overlap analysis was conducted for TLEs of COMS over a month, and Fig. 13 shows the results in the form of the position and velocity. The position error is on the order of tens of kilometers, which corresponds to about 0.1 degrees of angular error at an altitude of 35,790 km and is similar to the position error in the TLE information (Tombasco et al. 2011).

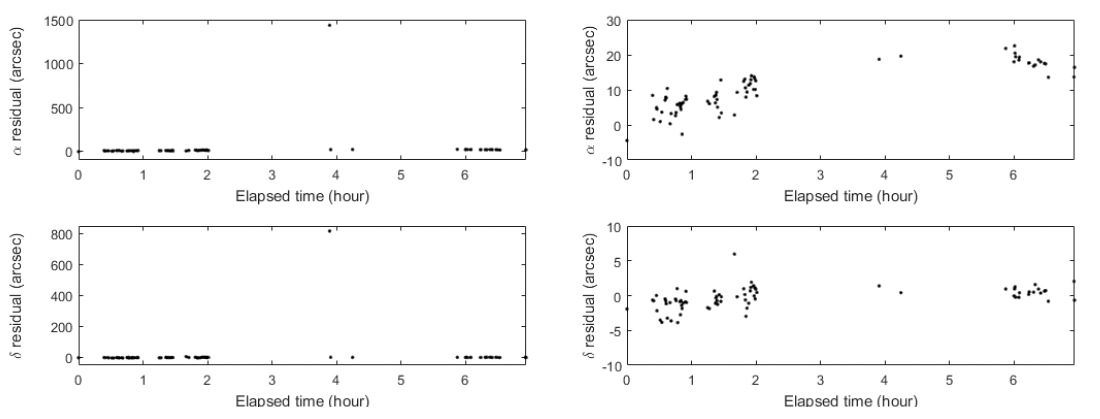
TLE is also assessed by the measurement residual from the actual tracking of COMS from OWL-Net (Fig. 14). The typical residual values are tens of arcseconds, excepting the irregular jump to 0.1 degrees at about four hours after the observations started. The residuals correspond to a position error of several kilometers, which coincides with the overlap analysis, and it is thus confirmed that TLE has several kilometers of position accuracy.

The orbit solutions were obtained under the conditions listed in Table 3, by using the OWL-Net data of two different arc lengths: 2 and 7 hours. The epoch time was set as the first observation time, and the a priori state vector was obtained by propagating TLE from the TLE epoch to the observation epoch, i.e., about 11 hours and 30 minutes. Note that the irregular data in Fig. 14 were excluded from the OD by a 3-sigma editor.

Fig. 15 shows the post-fit residuals of zero-mean with standard deviations of 2.8 arcseconds for RA and 1.4 arcseconds for DEC in both arc cases. These residuals are consistent with the known quality of OWL-Net observations of a few arcseconds (Choi et al. 2018), which indicates that the estimated state is well converged to the true state. It verifies both the quality of the OWL-Net data and the applicability of the developed software to the actual system. According to the numerical simulations in Section 3.4, the positional accuracy of the orbit solution is expected to be about 1 km using such quality of optical data.

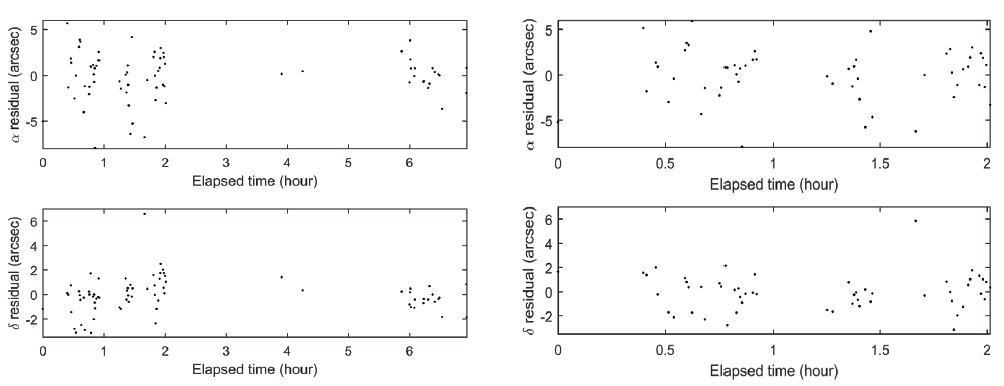
Table 4 addresses the Cartesian differences of the OD results with respect to TLE in topocentric radial-transversenormal (RTN) coordinates. The positional differences are about 16.97 km with the short arc and 1.38 km with the long arc, and the differences in velocity are 1.13 m/s with the short arc and 0.17 m/s with the long arc. The differences are smaller for longer arc length, which is consistent with the previous analysis in Section 3.1. Moreover, the largest portion of the positional difference is in the radial direction, which reflects the characteristics of the optical system that only measures the projected angle of the celestial sphere. In both cases, the OD accuracy is reasonable considering the TLE accuracy of several tens of kilometers, and the accuracy is also consistent with a previous study of the OD for COMS using OWL-Net data (Choi et al. 2015).

Table 5 presents the differences between the OD results and TLE in the form of the orbital elements. The differences in the semi-major axis, eccentricity, and inclination decrease considerably as the arc length increases: the relative errors vary from 0.1% to 0.004% for the semi-major axis, more than 800% to 30% for the eccentricity, and from 27% to 0.2% for the inclination. The true longitude, which is typically applied in equatorial and circular orbits, however, had a relative error of under 0.01% in both cases. This can be explained by the fact that the velocity accuracy improves as the arc length increases, so the elements which depend strongly on the velocity are considerably corrected.

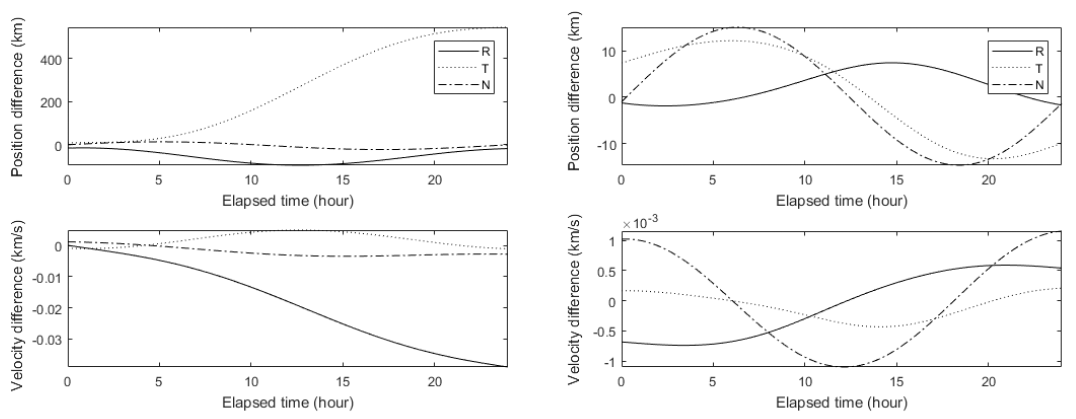
Both orbit solutions were propagated for 24 hours and compared to TLE to evaluate the orbit prediction accuracy after a day. Fig. 16 shows the differences in position and velocity in topocentric RTN coordinates. The prediction accuracy of the long arc solution was 20 times better than that of the short arc solution; the positional differences were hundreds of kilometers in the short arc cases and about 20 km in the long arc case for a day. Considering the field of view of OWL-Net, which is 1.75 degrees (Park et al. 2013), it is confirmed that OWL-Net data with an arc length longer than 2 hours can provide accurate orbit solutions to continue monitoring GEO satellites for a day.