1 INTRODUCTION
The symbiotic star is a binary system consisting of a cold red giant star (GS), a hot white dwarf (WD), and a surrounding ionized nebula of electrons with a temperature of about 15,000 K and electron density of 106-109 cm-3. In general, the nebula in a symbiotic star is photo-ionized by the ultraviolet radiation of the hot white dwarf and is considered to produce various emission lines including permitted lines, forbidden lines, and quasi-forbidden lines. AG Peg, which produces this variety of emission lines, shows four characteristics in its structure: an unresolved central body with an angular diameter < 0.1″, inner nebula with diameter of 2″, intermediate nebula with a diameter of 20″, and outer bipolar nebula with a dispersion angle of 1′ (Kenny & Taylor 2007).
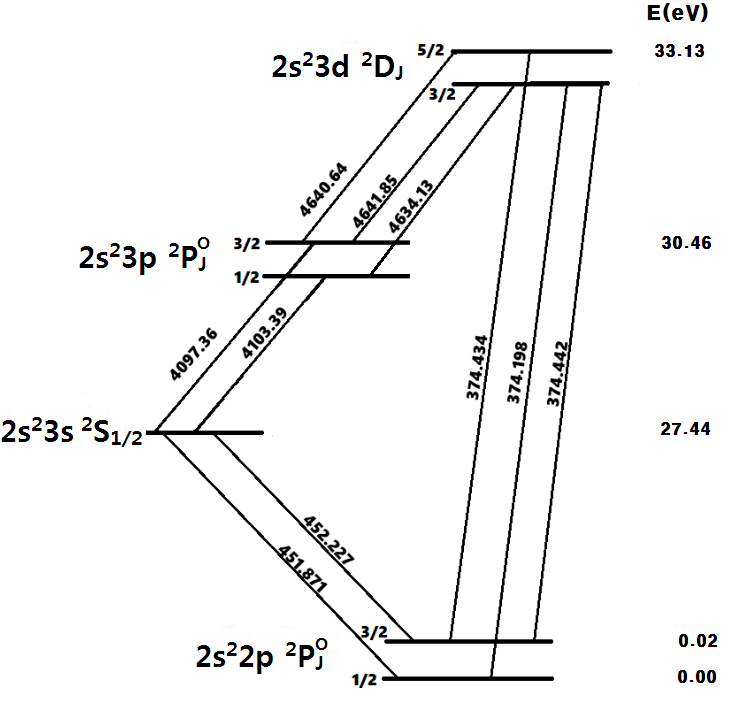
Among these emission lines, N III lines in the visible range are observed with a strong intensity in a symbiotic star like AG Peg and in a planetary nebula. The strongly registered O III lines have been considered to be He II fluorescence lines from the UV He II line, named O III Bowen lines after the researcher who first reported them (Bowen 1934, 1935). Later, many other channels were found. One of them is an O III fluorescence mechanism, resulting from the line matching of O III λ 374.436 (2p3s 3P1-2p23P2) and N III λλ 374.434, 374.442, similar to the line matching principle of He II λ 303.780 (2p 2P-1s 2S) and O III λ 303.799 (2p3d 3P-2p23P). In this scenario, other N III lines are not observed while λλ 4,097.31, 4,103.37, 4,634.16, and 4,640.64 lines are observed in a planetary nebula.
Fig. 1 shows a diagram with possible Bowen N III transition lines associated with Bowen O III λ 374.432 lines. In O III photo-excitation λ 374.432, a transition occurs from the level to the levels of N III 3d 2D3/2 and 3d 2D5/2. Lines at λλ 4,634.13, 4,640.64, and 4,641.85 are emitted by decay from these two levels, and λ 4,097.36 and λ 4,103.39 are emitted from the subsequent decay. The energy levels corresponding to each level shown in Fig. 1 are further explained in Table 1.
Beginning with the study of the Bowen fluorescence mechanism (BFM) model on planetary nebulae in 1940s and 1950s, research on the efficiency of the BFM and comparison of the BFM model with observations have been actively performed since the early 2000s. Among these studies, research on the O III Bowen lines of planetary nebulae has been the primary focus. However, in the 1970s, there were debates on the cause of the formation of bright N III emission lines in the range of λ 4,634-4,642 Å in an X-ray binary star between the electron recombination after separation (Mihalas & Hummer 1973) and Bowen mechanism (McClintock et al. 1975). Kallman & McCray (1980) performed a theoretical calculation of the Bowen fluorescence mechanism and discussed it based on a comparison with O III and N III line intensities observed in planetary nebulae and X-ray binary stars. They reported that there is good agreement between the model and the observation in planetary nebulae, but analyzing the line intensities observed in the nebulae surrounding X-ray binary stars is complicated and involves various uncertainties. Kastner & Bhatia (1991) proposed that the N III 4,640 Å multi-lines of the 3d-3p transition and the N III 4,100 Å multi-lines of the 3d- 3s transition observed in planetary nebulae do not result from the O III-N III Bowen mechanism. However, they do result from the thermal Boltzmann distribution, as the relative line intensity ratio of N III is in good agreement with that of the statistical weight. Later, Ferland (1992) discussed that since the estimated line intensity of N III λ 4,634.13 through the calculation of the photo-ionization structure model in a typical planetary nebula based on continuum fluorescence (CF) shows good agreement with the average value of line intensities for nine planetary nebulae suggested by Kastner & Bhatia (1991), CF could provide a good explanation for the observation of N III lines in the visible range. Eriksson et al. (2005) proposed a semi-empirical formula to estimate the relative intensity of N III resulting from the Bowen mechanism, assuming the Bowen mechanism is the only source of excitation to the N III 3d level. They made a comparison between the theoretical intensity and the observed intensity on AG Peg and predicted a relative line intensity ratio I4634/I4640 = 0.174, but the observed intensity was 0.433, showing a large discrepancy. Thus, they suggested that radiation recombination along with the Bowen mechanism contributes to the excitation of N III 3d in AG Peg. Selvelli et al. (2007) argued that in the Bowen line study of RR Tel, recombination and CF could not explain the excitation of N III λ 4,640.64. They reasoned that line fluorescence (LF) was the only mechanism of excitation, and the role of multiple scattering in the resonance lines of O III and N III near λ 374 was of great importance. They also suggested that the observed ratio of relative line intensity to absolute intensity of N III could be explained by LF due to the O III resonance lines of λλ 374.073, 374.162, 374.432 under optically thick conditions.
Most of the studies performed previously (Saraph & Seaton 1980; Selvelli et al. 2007) concluded that the excitation of the O III line was caused by the line matching of He II Ly-α. However, studies on N III lines reached a completely different conclusion—the excitation was not caused by matching of the wavelength with the O III resonance lines (Kastner & Bhatia 1991; Ferland 1992). Moreover, while the N III 3d- 3p lines (λλ 4,634.14, 4,640.64, 4,641.85) and 3p-3s lines (λλ 4,097.36, 4,103.39) are observed in symbiotic stars, it is not clear whether these lines are the result of line matching of O III-N III or that some other mechanism is involved in the excitation to 3d. Besides, most of the solar objects that undergo excitation processes were planetary nebulae, and during these ten years, there was hardly any symbiotic star of interest to the research community, with very few detailed studies made.
In this study, we have analyzed the high dispersion spectroscopic N III emission lines of AG Peg observed at the Lick Observatory in the USA in three different epochs. We have studied the excitation mechanism by measuring the full width at half maximum (FWHM) and line intensity of N III lines for each epoch and comparing those with predictions. We have also calculated the incoming and outgoing photons at each level to get an idea how to take into account the energy balance.
2 OBSERVATION AND DATA REDUCTION
We have observed AG Peg, a symbiotic star, using the Hamilton Echelle Spectrograph (HES) mounted on the 3 m Shane telescope at the Lick Observatory in the USA. The standard star for flux calibration is chosen to be HR 7596 from the list of IRAF standard stars. HES has the capability of adjusting the size of the rectangular slit located on the focal plane of the Coude to a celestial object, and a 5˝×1.2˝ slit was used for the observation of AG Peg while a 5˝×1.8˝ slit was used for the observation of a standard star. In the observation of AG Peg, the slit size in the spatial direction is 5˝ while the slit size in the wavelength direction is 1.2˝. With this selection of slit size, the wavelength resolution is about 0.2 Å/pixel at 5,000 Å. The basic features of the telescope and HES used in the observation are summarized in Table 2.
| Instruments | Basic characteristics |
|---|---|
| Telescope | |
| HES |
For the detection of weak radiation such as Bowen lines and for the prevention of saturation of strong radiation such as from hydrogen lines, the exposure times were adjusted, respectively: 300 sec and 1,800 sec for 1998 data, 180 sec and 1,800 sec for 2001 data, and 300 sec and 3,600 sec for 2002 data. The typical seeing during the observation epochs were 1.5″ for 1998, 1.0″ for 2001, and 0.8″ for 2002, and spectroscopic data were obtained under good atmospheric conditions.
Generally, the eclipse timing can be predicted by the following simple equation
where C represents the eclipse timing, T0 indicates the starting point in Julian date format, P is the orbital period (day), and E is the number of revolutions. Therefore, the phase (Φ) of AG Peg at the time of observation can be obtained using the following equation
where, JDobs indicates the observation date in Julian date format. According to the ephemeris, when the GS eclipses the WD (the minimum brightness), the phase is defined as 0 (Φ = 0) (Lee et al. 2012). However, we have utilized JDMax(V) = JD 2,442,710.0 + 816.5·E suggested by Iben & Tutukov (1996), in reference to the maximum brightness, to calculate the orbital phase of AG Peg. Hence, in this study, when Φ = 0, maximum brightness occurs with the WD located in front of the GS, and when Φ = 0.5, minimum brightness occurs since the GS eclipses the WD. Table 3 shows the observation log of AG Peg and lists the time of observation, Julian date, observation phase, and wavelength range of observation.
| Observation date (year/month/day) | Julian date | Phase (Φ) | Region (Å) |
|---|---|---|---|
| 1998/09/17 | 2,451,073.70 | 0.24 | 3,480-10,300 |
| 2001/08/30 | 2,452,151.60 | 0.56 | 3,480-10,650 |
| 2002/08/11 | 2,452,498.92 | 0.98 | 3,400-9,925 |
AG Peg spectroscopic data were processed in accordance with the standard data processing sequence of the image reduction and analysis facilities (IRAF) in the National Optical Astronomy Observatory (NOAO). First, ZERO calibration was performed, followed by DARK calibration and a flux calibration. From the final fit file obtained, parameters including the central wavelength, flux, and FWHM (Å) were measured through the IRAF splot task. In the AG Peg center of mass system (0 km·s-1), since emission line data composed of principal velocity and flux are needed, wavelengths were converted into velocities through the following process and were analyzed in StarLink DIPSO of ESO.
-
Task 1) IRAF scopy task: extract the spectrum with the necessary aperture
-
Task 2) listpix task: save the wavelength of specific line contour and flux values
-
Task 3) IDL Program: convert heliocentric radial velocity and flux to text files
-
Task 4) DIPSO: FWHM (km·s-1) and flux measurement through Gaussian fitting
Wavelength and flux data processed with Tasks 1) and 2) in the server were transmitted to a PC for further processing with Task 3). Because the time of observation is different for the spectrum data in 1998, 2001, and 2002, comparing the line contour and the radial velocity requires compensation for the rotation and revolution of the Earth. Thus, for the data on Sep. 17, 1998 (φ = 0.24), Hα with an exposure time of 300 sec was corrected by Vhelio = -9.16 km·s-1 while the other lines with exposure time of 1,800 sec were compensated by Vhelio = -9.22 km·s-1. Similarly, it was determined that for the data on Aug. 30, 2001 (Φ = 0.56), Vhelio = -1.79 km·s-1 for an exposure time of 180 sec, and for the data on Aug. 11, 2002 (Φ = 0.98), Vhelio = -7.05 km·s-1 for an exposure time of 300 sec. In addition, the heliocentric radial velocity of AG Peg, -17.09 ± 3.32 km·s-1 (Lee et al. 2017), was also compensated to obtain the final compensated velocity and flux. In Task 3) in which the IDL program is used, the contour of the principal lines in the center of mass system of AG Peg (0 km·s-1) was displayed on the PC screen, facilitating the determination of the anomaly of the line profile. In Task 4), the final text file of compensated velocity and flux was transmitted to the server, and the components were analyzed through DIPSO to measure FWHMs (km·s-1) and fluxes. In this case, it should be noted that the measured flux through DIPSO, in which the horizontal axis represents velocity, differs from the measured flux in the IRAF splot task, in which the horizontal axis indicates wavelength. Thus, when it is necessary to use velocity and flux measured through DIPSO, for each emission line, the velocity corresponding to 1 Å should be calculated and the measured flux should be divided by this velocity.
3 N III EMISSION LINE ANALYSIS
To compare FWHMs and line intensities of N III Bowen lines, we have examined N III ordinary lines. The intensities of ordinary N III lines are generally very weak, and some lines were not measurable in a specific epoch. The detected lines are λλ 3,745.95 (3p 4S3/2→3s ), 4,195.74 (3p 2D3/2→3s 2Po 1/2), 4,379.11 (5g 2G→4f 2F), 4,510.88 (3p 4D3/2→3s ), 4,518.14 (3p 4D1/2→3s ), 4,523.56 (3p 4D3/2→3s ), 4,534.58 (3p 4D5/2→3s ), and 4,544.84 (5s 2S1/2→4p ). The transition of 4,379.11 was obtained from Feklistova & Kholtygin (1997), and the others were obtained from National Institute of Standards and Technology (NIST, http://physics.nist.gov/ PhysRefData/ASD/lines_form.html). The wavelength range of N III Bowen lines is 4,000-4,700 Å, and as shown in the 1998 spectrum in Fig. 2, we have found a total of five Bowen lines marked by arrows, including λ 4,103.39 located in the right edge of Hδ λ 4,101.74. Similar to the 1998 data, five N III lines appeared in 2001 and 2002. Eriksson et al. (2005) reported that in AG Peg, they could not observe six O III Bowen lines, but they observed five N III Bowen lines, consistent with our findings.
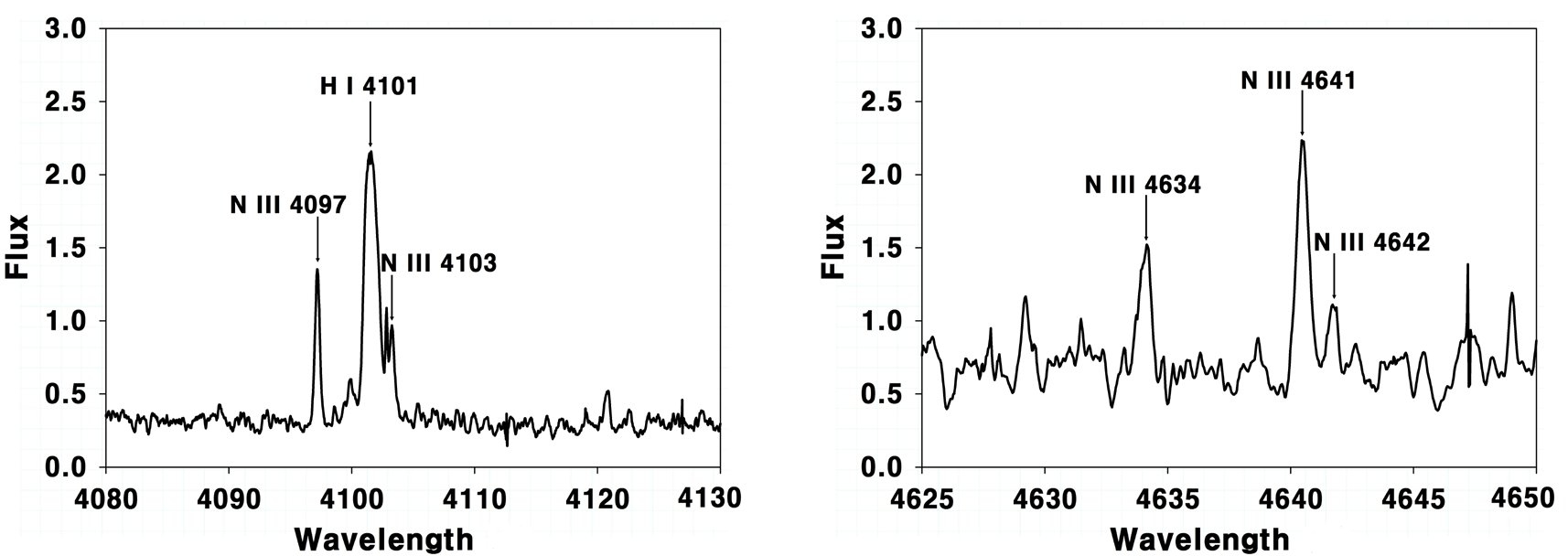
We have measured FWHMs of N III Bowen lines for 1998, 2001, and 2002, by Gaussian fitting through StarLink DIPSO, made by ESO (European Southern Observatory). However, in some cases, N III ordinary lines were too weak to analyze the components using DIPSO. Thus, we have measured FWHMs using IRAF splot. The FWHMs measured through DIPSO or IRAF splot include the increment of FWHMs induced by other external factors. Since electron temperatures at three epochs are different from each other, thermal FWHM increments (Vth) were obtained considering electron temperatures. Moreover, FWHM increments due to fine structure (Vf-s), instrumental factors induced by the spectrometer and telescope (Vinst), and the turbulence (Vturb) were obtained. Detailed calculation procedures are described in Lee & Hyung (2007). Also, the final FWHMs (or pure kinematical line broadening width) calculated by 2Vexp = (VFWHM2 - Vth2 - Vinst - Vf-s2 - Vturb2)1/2 are shown in Table 4. As can be seen in Fig. 2, the measured FWHM of λ 4,103.39 by using DIPSO is not clear because it is located in the right edge of the strong Hδ λ 4,101.74 line, overlapping together. In the latest study, Eriksson et al. (2005) reported that they found five N III lines in AG Peg but did not indicate the FWHM. Hence, the FWHMs measured in RR Tel of the symbiotic star (Selvelli et al. 2007) are shown in Table 4 for comparison.
The average FWHM of N III ordinary lines was 41.0 km·s-1, 34.2 km·s-1, and 38.2 km·s-1 for the data of 1998, 2001, and 2002, respectively. There were no common N III ordinary lines for the three epochs, and the lines were weak, showing a large discrepancy that included large uncertainties. Comparing the FWHMs with those of Bowen lines is difficult. However, contrary to our expectation, the FWHMs of N III Bowen lines are not greater than those of ordinary lines and was smaller by about 5 km·s-1 in 1998 and 2002. For the same epochs, the average FWHM of O III Bowen lines was 35.8 km·s-1, 24.1 km·s-1, and 33.0 km·s-1 for 1998, 2001, and 2002, respectively. We can see that the average FWHMs are similar to the average FWHMs of N III Bowen lines in 1998 and 2002. However, in 2001, the average FWHM of N III Bowen lines was greater by about 15 km·s-1. The large difference is likely to be caused by either the variation in the gas inflow rate from the giant star to the accretion disk around the WD or the WD stellar wind activity along its polar axis. The FWHM average for the three epochs was 35.8 km·s-1, which was greater by about 5 km·s-1 than the average FWHM of the O III Bowen lines for the same period.
We have measured the intensities of N III Ordinary Lines and Bowen Lines for the three epochs, using IRAF splot. The intensities were corrected by the extinction coefficient, C = 0.04 (Kim & Hyung 2008), to obtain the corrected intensities. For a similar reason similar to what is discussed about FWHMs in the previous section, while it is difficult to compare the measured intensities of ordinary lines and Bowen lines, the intensities of Bowen lines are generally greater by 5-8 times than those of ordinary lines (not presented in Table 5).
Ref.: HA = Hyung & Aller (1995), Mc = McKenna et al. (1997), Er = Eriksson et al. (2005), Sel = Selvelli et al. (2007), FL = Fang & Liu (2011).
Ipred is the calculated statistical intensity by Eriksson et al. (2005). See the text.
The results of previous studies on other objects are shown in Table 5 together with relative intensities predicted by Eriksson et al. (2005). The line intensities in Table 5 are relative intensities calculated with the line intensity of λ 4,640.64 set equal to 1.000. The intensity of λ 4,103.39 is not so accurate since it is located at the right edge of the strong Hδ λ 4,101.74 line, overlapping together. Eriksson et al. (2005) calculated the predicted intensity (Ipred), a statistical intensity, through a six-stage semi-empirical formula, assuming that all N III lines were generated by the Bowen mechanism. On the whole, the observed values were greater than Ipred.
The suggested theories for the excitation mechanism of N III lines are LF, radiation recombination, and CF. While Eriksson et al. (2005) predicted I4634/I4640 to be 0.174 in AG Peg, this value is significantly smaller than the measured intensity ratio, I4634/I4640 = 0.433. They made an assertion that since the measured intensity ratio exhibits a large difference from the AG Peg theory, radiation recombination contributed to the excitation of N III lines, in addition to LF. The Bowen process requires resonance lines of high optical thickness (τ0) (Selvelli et al. 2007). However, the semi-empirical formula, which Eriksson et al. (2005) used for the prediction of theoretical intensity, did not account for the average scattering number, , a function of τ0, and assumed that all transitions were optically thin. For this reason, it is believed that a low value of intensity was predicted. In this study, the values of I4634/I4640 in AG Peg obtained from observations are 0.537, 0.562, and 0.557 for 1998, 2001, and 2002, respectively, as all values are relatively equal. Also, results from other investigations on I4634/I4640 produced values similar to 0.5.
Ferland (1992) performed calculations of a photo-ionization model through CF and reported that the intensity of N III 4,634.14 agreed well with the measured one. Thus, he made an argument that the three N III lines around λ 4,640 were the results of CF. Meanwhile, if CF contributed to N III λλ 374.198, 374.434, and 374.442 and produced three N III lines around λ 4,640, emission lines should be generated between 1,380- 4,890 Å for other N III extreme UVs (resonance lines of similar transition probability as λ 374 lines) (Selvelli et al. 2007). Hence, we have examined λλ 4,201.26, 4,855.16, 4,874.46, and 4,882.03, corresponding to the visible light range in our observation wavelength band for all three epochs, but we could not get any results. In other words, if N III 4,640.64 of the strongest intensity was influenced by the flux from a hightemperature central star, λλ 4,201.26, 4,855.19, 4,874.46, and 4,882.03 should appear in the visible light range, which did not agree with our spectroscopic observation data. This suggests that CF is not the contributor of excitation mechanism of N III lines. The description for the LF is given in Section 3.5.
In this section, we have predicted the intensities of O III and N III resonance lines around λ 374 and examined the amount of contribution by LF. First, when the Gaussian function is the normal distribution, we have calculated a using the correlation: area = , where a indicates the maximum intensity, c indicates the area under the curve, and the correlation of FWHM = 2.35482c holds true. In order to calculate c, we have utilized the average value of O III FWHM, 31 km·s-1, and the average value of N III FWHM, 35.8 km·s-1, for the three epochs of observation. As Aij, which represents the transition probability between the two levels, is related to the line intensity, the Aij value shown in Table 6 is put into the area to calculate the maximum intensity, a. We have set the intensity of N III λ 374.434, whose Aij is the maximum, at 100 and calculated the relative intensities of O III λ 374 and N III λ 374. Next, using the Gaussian function,
we have plotted relative intensities, as shown in Fig. 3. In Eq. (3), b indicates the central wavelength and a and c have the same meaning described above. The value 0 km·s-1 on the horizontal axis of Fig. 3 corresponds to λ 374.000. Since O III λ 373.803 shows a velocity difference of over 160 km·s-1 with λ 374.004, it was excluded.
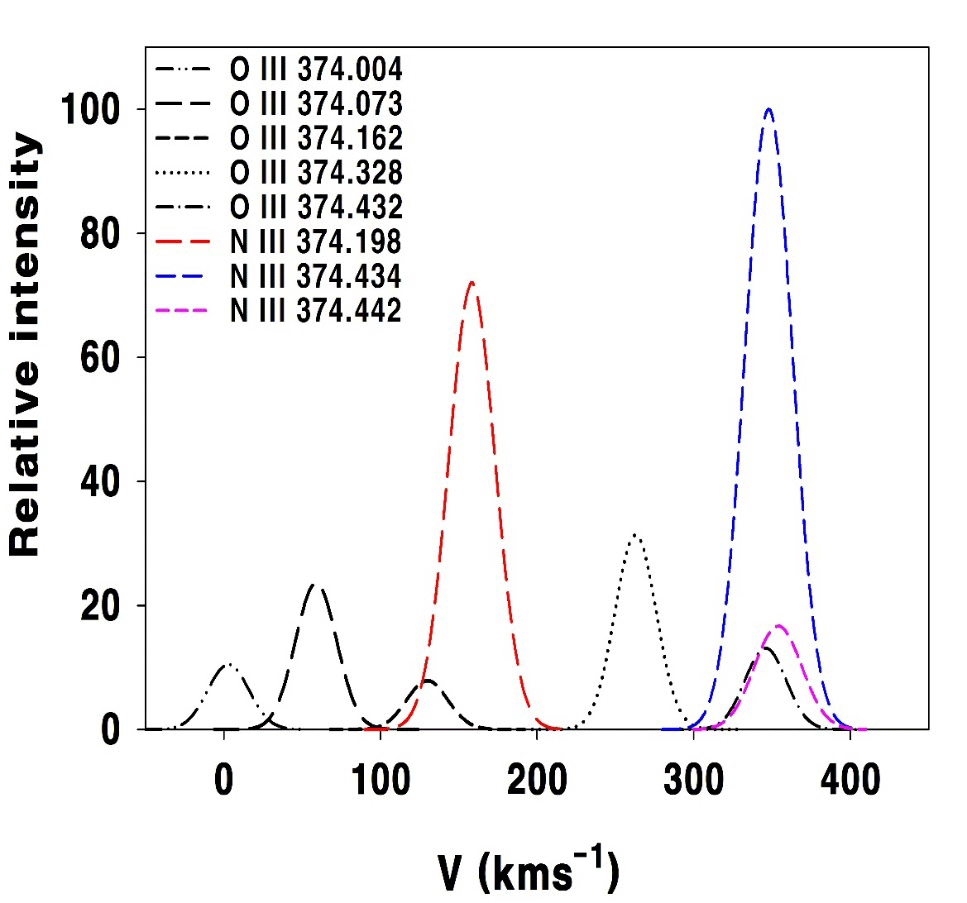
However, in Fig. 3, the intensities of five O III λ 374 lines are much smaller than the intensities of three N III λ 374 lines. That is, while the velocity difference between O III λ 374.162 and N III λ 374.198 is about 29 km·s-1 and overlap is possible, the intensity of O III λ 374.162 is only 10.9 % of the N III λ 374.198 intensity. Also, as the velocity of O III λ 374.432 differs from those of N III λ 374.434, N III λ 374.442 by 2 km·s-1, 8 km·s-1, respectively, excitation is possible on account of almost perfect line matching. While the intensity of O III λ 374.432 is almost the same as that of N III λ 374.442, and it could contribute to the excitation to the level of 2s23d 2D 3/2, as the intensity of O III λ 374.432 is only 13.1 % of the N III λ 374.434 intensity, the excitation to the level of 2s23d 2D is not possible. Thus, as the expected intensity through Aij described previously cannot explain the reason why O III λλ 374.162, 374.432 excites N III λλ 374.198, of contribution by LF. First, when the Gaussian function is the normal dist_ribution, we have calculated a using the correlation: 374.434, 374.442 to the levels of 2s23d 2D3/2 and 2s23d 2D5/2, we have considered other possibilities.
According to the results of the comparison between our three-year observation data and the observation data of Selvelli et al. (2007), the intensities of the N III Bowen lines are greater than those of the O III Bowen lines. Considering only the 1998 data of this study reveals that the intensities of five N III Bowen lines are 2.2 times greater than those of the O III Bowen lines in 3,750-3,800 Å. The measured intensity data of the O III Bowen lines were obtained from Hyung et al. (2017). The Grotrian diagram, which represents the transition of O III Bowen lines, explains why the intensities of N III Bowen lines are stronger (Hyung et al. 2017). The Aij of the first transition line indicates that the Aijs of O III λ 3,444.06 and O III λ 3,132.79 are quite large, and the contribution to the line intensity by these two lines is about 88 %. In addition, including the contribution of O III λ 3,428.62 adds up to about 92 %, and these decay to 6 O III lines around λ 374, which makes the intensity of resonance lines very strong. The Aijs of other emission lines (O III λλ 2,836.28, 2,818.66, and 2,807.90) of the first decay are about 8 %, and these lines contribute to the O III Bowen lines. Thus, the intensities of the O III Bowen lines are weak.
Note that the He II lines are also an important fluorescence source. The other UV He II 303 line eventually goes down to another optical channel, such as He II λ 4,685.68 (see Hyung et al. 2017). From the measured intensity of He II λ 4,685.68, we can estimate the intensity of He II Ly-α (λ 303.783) (Storey & Hummer 1995). In this study, due to the line matching between the estimated He II Ly-α and O III λ 303.800, the entire amount of the estimated intensity of He II Ly-α, which is about 1 %, is assumed to transfer to O III λ 303.800. Then, we can calculate the theoretical intensity of six O III resonance lines around λ 374 emitted from the first decay, second decay, and final third decay based on the transition and Aij ratio, according to Grotrian diagram. As a result of the calculation of the theoretical intensities of O III resonance lines, the intensity of O III λ 374.073 was the strongest, the intensity of O III λ 374.162 was the weakest, and the intensity of λ 374.073 was 5.7 times stronger than that of λ 374.162.
We have calculated the expected intensities of three N III lines λλ 374.198, 374.434, and 374.442, contributing to the intensity of N III Bowen lines described below. Among the emitting lines from the first decay, O III λ 3,444.06 was observed from the 2002 observation data only and the fraction of transition probability Aij was 22.5 %. The other UV lines of first decay were not observable since those were out of the observation wavelength range. Thus, in order to make the observation intensity of O III λ 3,444.06 100 %, the observed intensity was multiplied by 4.4 to produce the intensity of 4.74×10-11 erg·cm-2s-1. However, the sum of the intensity of five N III Bowen lines observed were 4.89×10-12 erg·cm-2s-1. The ratio of the observed intensity of O III λ 3,444.06 multiplied by 4.4 to the sum of five N III Bowen line intensities were 1:0.103. Thus, 10.3 % of total intensity of five O III λ 374 resonance lines, with the exception of O III λ 373.803, contributed to the three N III resonance lines, and it was assumed that the ratio was proportional to Aij. For the 1998 data, the intensity of eight resonance lines of O III and N III were estimated. As a result, the intensity of O III λ 374.073 was the strongest, and the intensity of N III λ 374.442 was the weakest, with the ratio of two lines equal to 60.6. In Fig. 4, the eight intensity curves of O III resonance lines and N III resonance lines are shown using the average of the O III FWHM, 31 km·s-1, and the average of the N III FWHM, 35.8 km·s-1, and utilizing the Gaussian function. Fig. 4 represents the relative intensities with the strongest O III λ 374.073 set to 100. Only O III λ 374.162 contributed to N III λ 374.198, and the overlap between the two lines are 33 %. While the wavelength of N III λλ 374.434 and 374.442 matched O III λ 374.432 with almost 100 % agreement, there was a big difference in line intensities. In the case of 100 % wavelength match, the expected intensity of N III resonance lines was obtained considering the overlap fraction by line intensity ratio.
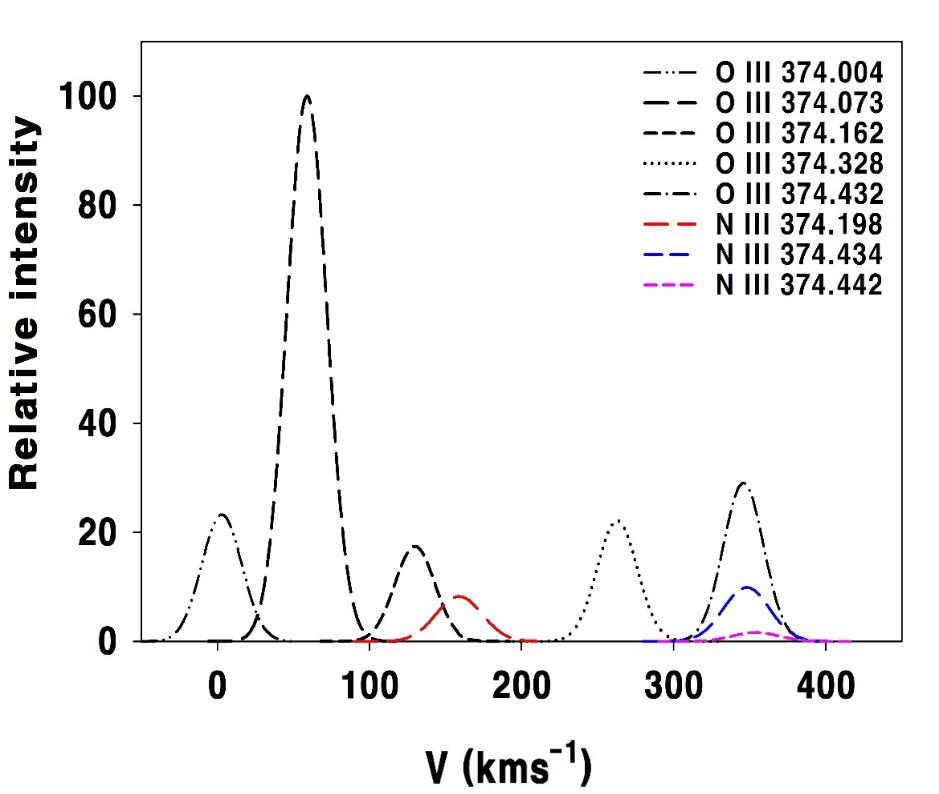
As described above, in Fig. 4, O III λ 374.004 and λ 374.073 never contribute to N III λ 374.198, and only O III λ 374.162 makes a contribution. Hence, the excitation effect from 2s22p EQ to 2s23d 22D3/2, due to the line matching of O III λ 374.162 and N III λ 374.198, depends on the overlap between the two lines. For N III λ 374.434 and λ 374.442, O III λ 374.432 makes almost 100 % contribution. Thus, the excitation from the level of 2s22p to the levels of 2s23d 22D3/2 and 2s23d 2D5/2 can be explained with ease by the complete overlap between O III λ 374.432 and N III λ 374.434 or N III λ 374.442. On this basis, the assertion that LF is not effective (Eriksson et al. 2005) seems to be based upon the tiny line overlap between O III λ 374.162 and N III λ 374.198, which could not make up for the excitation energy to 2s23d 22D3/2. This does not look reasonable.
If it is true that the excitation mechanism of N III Bowen lines is LF due to line matching, FWHMs play an important role in the excitation in addition to the wavelength match of resonance lines of O III and N III around λ 374. When the FWHM of resonance lines becomes greater than the observed average FWHMs for O III and N III and, also, when the other O III resonance lines, excluding O III λ 374.162 and O III λ 374.432, have small overlaps on the edge, they can contribute to the line intensity, though perhaps insignificantly. We could not obtain the FWHM data for O III resonance lines. In most cases, the FWHM of resonance lines are broader than those of recombination lines or quasicombination lines, due to the increase in FWHM resulting from the Doppler effect (Selvelli et al. 2007). Oegerle et al. (1983) suggested that the opacity broadening of resonance lines is proportional to and has a large impact on the contour of lines. If the optical thickness (τ0) of the line center is in the range of 103-107, the FWHM will be 2.6-4.0 times greater than that for optically thin cases. Although our study was not carried out using the exact value of opacity and optical thickness at the line center, the present work was largely based on an optically thick assumption.
The efficiency of N III Bowen lines, R, indicates the conversion ratio of O III resonance line photons into Bowen line photons around N III λ 4,640. R can be calculated easily from the intensity ratio of the strongest O III Bowen lines (λ 3,132.79 or λ 3,444.06) to N III Bowen lines (λ 4,634.14, λλ 4,640.64, and λ 4,641.85). Kallman & McCray (1980) calculated R for 18 planetary nebulae, and they were in the wide range of 0.23-1.56. They also expressed the efficiency, R, of N III Bowen lines by the observed intensity ratio of O III λ 3,444.06 and N III λλ 4,634.14 and 4,640.64
In this study, we could only calculate R for the 2002 data in which O III λ 3,444.06 (I = 107.8×10-13 erg·cm-2sec-1) was measured, and R of AG Peg obtained from the Eq. (4) was 0.50. The R calculated using the photon number (Nν) of O III λ 3,444.06 (Nν = 1.869 cm-2sec-1), N III λ 4,634.14 (Nν = 0.188 cm-2s-1), and N III λ 4,640.64 (Nν = 0.337 cm-2s-1), which were converted from line intensities, was 0.67, which was slightly higher. Meanwhile, Selvelli et al. (2007) calculated R of RR Tel to be 0.48. The efficiency of AG Peg being higher than RR Tel implies that the ionized shell of the former consists of much higher gas density, causing a large optical depth.
Based on the expected intensities for the resonance lines of N III λλ 374.198, 374.434, and 374.442 discussed in the previous section, we have calculated the expected intensity (Ipred) of N III Bowen lines, which experiences a lower transition with transition probability, Aij, using the N III Grotrian diagram in Fig. 1. When calculating the expected intensity of 4,097.36 and 4,103.39, extreme UVs whose Aijs were large enough to impact the expected intensity were considered for those transitioning from the same level. In other words, for 4,097.36, the Aij of extreme UVs, λλ 691.193 and 871.862, transitioning from the same level, were considered, and for 4,103.39, the Aij of extreme UVs, λλ 691.397 and 872.135, transitioning from the same level, were considered.
We did not calculate the theoretical expected intensities for the three observation epochs because the positions and the line intensities of GS and WD are different, depending on the phase of a symbiotic star, AG Peg. Only for 1998, when the phase was 0.24, were both GS and WD visible, and the expected intensities (Ipred and Irelpred) were obtained, as shown in Table 7. As mentioned above, Eriksson et al. (2005) obtained the ratio of expected intensities for AG Peg as I4634/ I4640 = 0.174 and argued that LF was not effective since the ratio was too small compared to the ratio of observed line intensities, 0.433. Selvelli et al. (2007) obtained the expected line intensity ratio I4634/I4640 = 0.09 under the assumption that the level 2s23d2P3/2 excitation was possible only by N III λ 374.442. As this value was less than the observed ratio of line intensity, 0.49, they made an assertion that O III λ 374.073 and λ 374.328 had an impact. However, in this study, since the observed line intensity ratio, I4634/I4640 = 0.537 for 1998 data was similar to the expected line intensity ratio, 0.617, it appeared that λλ 374.004, 374.073, and 374.328 had an impact in addition to O III λ 374.162 and λ 374.432, and it was confirmed that the excitation mechanism was LF.
To find out the energy balance in the N III transition, the photon number of N III emission lines, related to the Bowen fluorescence shown in the AG Peg spectrum, was calculated and summarized in Table 7, together with transition probability, Aij, according to the wavelength.
Two lines formed by this transition are N III λ 4,640.64 and λ 4,641.85, and these two lines are the parent line of N III λ 4,097.36, which is formed by the transition from EQ to 2s23s 2S1/2. The ratio of the sum of the photon number (Nν) of N III λ 4,640.64 and λ 4,641.85 to the photon number of λ 4,097.36 were 2.72, 1.99, and 1.63 for 1998, 2001, and 2002, respectively, and the average was 2.12. While the number of incoming and outgoing photons should be the same, a ratio of about 2 indicates that as there is no other parent line of N III λ 4,097.36, except for N III λ 4,640.64 and λ 4,641.85, there should be another transition line to generate N III λ 4,097.36. According to the investigation result of NIST, there were N III λ 691.193 (2s23p -2s2p22D5/2; Aij = 9.22×107 sec-1) and λ 871.862 (2s23p -2s2p2 2S1/2; Aij = 3.84×107 sec-1), transitioning from 2s23p . When the sum of the Aijs for these two lines is two times the Aij of N III λ 4,097.36, the photon number ratio will be the same, but it was 1.50 in this case. This value differs significantly from the ratio of photons obtained from the measurement in 1998 but agrees well with the ratio of photons obtained in 2002. Therefore, when we consider the Aij of N III λ 691.193 and λ 871.862, it could be concluded that the number of incoming and outgoing photons obtained from observation are in equilibrium.
The transition from 2s23d 22D3/2 to 2s23p forms N III λ 4,634.14 and λ 4,641.85. These two lines are formed by a lower transition from the upper level 2s23d 22D3/2 and, as shown in Table 7, the Aij ratio is 5.05 and the observed line intensity ratio (I4634.13/I4641.85) should be close to 5.05. However, as we can see in Table 5, I4634.13/I4641.85 ranges widely depending on the celestial body of interest in the previous studies. In the result of Fang & Liu (2011), the value calculated turned out to be 5.01 and 5.02, which is quite close to the current value. However, the result of Eriksson et al. (2005) was 10.31, which is more than two times greater, and the results of Hyung & Aller (1995) and McKenna et al. (1997) were about half of the current value. Selvelli et al. (2007) got the ratio of 3.50 and explained that the reason why it was slightly lower is the fact that the FWHM (33.7 km·s-1) of N III λ 4,641.85 is slightly broader than the FWHM (31.8 km·s-1) of 4,640.64 and there is a partial overlap. In our study of 1998, 2001, and 2002 data, the line profile around N III 4,640.64 indicates that N III λ 4,640.64 and λ 4,641.85 show an overlap, and as shown in Table 4, the FWHMs of 1998 and 2002 data are similar to each other, and, in 2001 data, the FWHM of N III λ 4,641.85 is about 16 km·s-1 broader. Hence, it is believed that the average of I4,634.13/I4,641.85 observed for three epochs show a low value of 2.1.
The line formed by this transition is N III λ 4,103.39 and the parent line is N III λ 4,634.13. As can be seen in Fig. 1, while N III λ 4,634.13 is the only feeding line, it is emitted from the level of 2s23p 2Po1/2 similar to N III λ 4,103.39, and there are two lines whose Aijs are large enough to have an impact on the line intensity and photons. These two lines are λ 691.397 (2s23p 2Po1/2-2s2p222D3/2; Aij = 1.02×108 sec-1) and λ 872.135 (2s23p 2Po1/2-2s2p2 2S1/2; Aij = 3.85×107 sec-1), and the sum of the Aij (1.405×108) of the two lines is 1.62 times greater than the Aij of λ 4,103.39 (8.67×107). Thus, N III λ 4,634.13 should be 1.62 times greater than λ 4,103.39 in terms of line intensity or the number of photons. However, the ratios of photons for the three epochs of our observation were 1.17, 0.84, and 0.80 for 1998, 2001, and 2002, respectively. These values seem too small, and it could be a reason that the intensity of N III λ 4,634.13 was measured too weak or the intensity of λ 4,103.39 was measured too strong. Although N III λ 4,634.13 is weak, it has single peak and the uncertainty is small. However, λ 4,103.39 is strong and is positioned in the right edge of Hδ λ 4,101.74, which shows a complicated line contour, it is apparent, thus, that the line intensity was measured quite incorrectly.
4 CONCLUSION
In this study, by analyzing the HES high dispersion spec-troscopic data of a symbiotic star, AG Peg, observed with the 3 m Shane optical telescope at Lick Observatory for three different epochs, we have studied the intensities and FWHMs of N III emission lines generated by the Bowen fluorescence mechanism.
For all three epochs, all five N III lines were clearly seen, but none of them appear to be an ordinary line. The average FWHM of N III Bowen lines for the three epochs was 35.9 km·s-1, but comparison to ordinary lines were not possible because there was almost no N III ordinary line for all three epochs. Furthermore, the intensity was very weak, resulting in large errors. The average FWHM of N III Bowen lines is about 5 km·s-1 wider than that of O III Bowen lines (FWHM of 31.0 km·s-1) for the three epochs. Also, while the comparison of intensities between ordinary lines and Bowen lines were difficult due to the reason described above, the intensity of the Bowen lines was a maximum of eight times stronger than that of ordinary lines. All of the Bowen processes require resonance lines with high optical thickness (τ0) since the prediction of theoretical intensity did not account for the average scattering number, . For comparison, we also presented the relative intensities of N III Bowen lines for NGC 7009 and RR Tel, other than what is exhibited by AG Peg, and made a comparison with data obtained from previous studies. According to the results, radiation recombination (Eriksson et al. 2005) and CF (Ferland 1992) are not appropriate for the excitation mechanism of N III lines, but LF best fits the mechanism.
To find out the contribution of the O III resonance lines around λ 374 to N III resonance lines by LF, the intensities were plotted using the Gaussian function. O III resonance lines are emitted from the third transition from He II-O III fluorescence. For this plot, we have used the FWHM of O III and N III Bowen lines obtained from the observation of FWHM for O III and N III resonance lines. As a result, we found that only O III λ 374.162 contributed to N III λ 374.198, and the fraction of contribution was about 33 %. Moreover, while the intensity was different, only O III λ 374.432 showed almost 100 % line matching with N III λ 374.434 and λ 374.442. However, if the FWHMs of the O III and N III resonance lines are greater than our observed values, the other three O III resonance lines other than O III λ 374.162 and λ 374.432 could overlap and contribute to the N III resonance lines. Thus, they could contribute to the expected intensity of N III Bowen lines.
We have estimated the intensities of three N III resonance lines and obtained the expected intensities of N III Bowen lines based on the N III Grotrian diagram and transition probability Aij. In this calculation, while there were extreme UVs transitioning from the same level with N III Bowen lines, extreme UVs with Aij that are too small were excluded, and extreme UVs with an Aij large enough to have an impact on the expected intensity of N III Bowen lines were taken into account. We have calculated the absolute expected intensities at the phase of 0.24, where both GS and WD are visible for only 1998 data, and compared it with the measured intensity. Our results show that all expected intensities are less than the measured intensity. Also, we have compared the relative intensity calculated with the intensity of N III λ 4,640.64 set to 1.000, with that of Eriksson et al. (2005) for AG Peg. For N III λ 4,634.14, the deviation was the largest; we have obtained an expected intensity of 0.617, while Eriksson et al. (2005) obtained an expected intensity of 0.174. The observed intensities of N III λ 4,634.14 were in the range of 0.4-0.6, according to the results of previous studies and this study. Considering that other earlier results are in a range between 0.4 and 0.6, the intensity of 0.174 calculated by Eriksson et al. (2005) appears to be mistaken.
Based on the spectroscopic observation data, the incoming and outgoing photons for each level of N III Bowen lines were calculated, and the photon number ratio of N III Bowen lines were higher or lower. The reason is speculated that outgoing extreme UVs (e.g., λλ 691.193, 871.862, etc) not shown in Fig. 1 were considered, or a part of N III Bowen lines observed were too close to other emission lines, resulting in an overlap of contours in the vicinity of strong emission lines, which caused an incorrect measurement of intensities. When we account for these effects, most of the ratios of photons agree well. However, for better understanding of the excitation mechanism of N III Bowen lines and the photon number balance, UV observation data in the range of 1,300-3,500 Å and accurate intensity measurements are required. We expect that satellite observation of high dispersion spectroscopic data in the UV range will be available in the future.
In this study, we have compared the theoretical expected intensities with the measured intensities for N III Bowen lines of AG Peg, and when the excitation mechanism of N III lines is believed to be Bowen fluorescence effects, we have performed analyses on the UV lines that had an impact on the line intensity, the transition of O III resonance lines for each electron orbit level in the UV range, and the photon number equilibrium of N III lines generated. This study could be beneficial to the research on the physical characteristics and evolution of other symbiotic stars where N III lines were observed.