1 INTRODUCTION
Since the first laser measurement of an artificial satellite made by the National Aeronautics and Space Administration (NASA) Goddard Space Flight Center (GSFC) in 1964, satellite laser ranging (SLR) has been one of the most precise range measurement techniques applicable to orbit determination (OD) of satellites (Plotkin et al. 1965). The single-shot accuracy of SLR over a single pass is about 5-50 mm, and the rootmean- square (RMS) of normal point (NP) data is known to have millimeter precision (Montenbruck & Gill 2000; Appleby et al. 2016). The SLR technique has been combined with other satellite tracking systems, such as the global positioning system (GPS), and the stand-alone SLR-based OD solution has been used for verification of satellite orbits estimated from microwave measurements to acquire centimeter-level bias for the global navigaion satellite system (GLONASS) satellite network (Urschl et al. 2005, 2007) and also has obtained a 20-40 cm difference from the international global navigation satellite system (GNSS) service (IGS) orbit for a GPS satellite (Zhu et al. 1997). A comparison between the SLR orbit and the precision orbit ephemeris (POE) by the Jet Propulsion Laboratory (JPL) showed a difference of less than 1 m for the TOPEX/POSEIDON and CHAMP satellites (Kim et al. 2009). Also, SLR-based OD has been performed for low- Earth-orbit (LEO) satellite with no GPS receiver (Kim et al. 2015). As many countries are developing their own satellite navigation system, such as the Chinese Compass/Beidou, Japanese quasi-zenith satellite system (QZSS), and Indian regional navigation satellite system (IRNSS), along with GPS and GLONASS, the SLR-based OD solution is being actively utilized for quality assessment of orbit precision (Otsubo et al. 2001; Montenbruck et al. 2013; Maier et al. 2015; Sośnica et al. 2015).
Although most SLR target satellites are located below mid- Earth-orbit (MEO), SLR tracking of high-Earth-orbit (HEO) satellites remains challenging. Because of the limited orbit coverage of HEO satellites, the number of SLR tracking data is usually not sufficient, in contrast to the case of LEO satellites. Also, the laser intensity of some existing SLR tracking stations is not sufficient to observe HEO satellites because of the long distance between ground tracking stations and the target satellite. Furthermore, the bin size of NP data for HEO satellites is 300 sec, whereas MEO satellites, such as Laser Geodynamics Satellite -1 and -2 (LAGEOS-1, LAGEOS-2), have a bin size of 120 sec due to their relatively lower altitudes. This difference in bin size is prevalent because more condensing time of raw data points is required to generate the NP data for satellites at higher altitude, and this causes a relative decrease in the number of NP data of HEO satellites for the same tracking period compared with the case of MEO or LEO satellites. These problems lead to a lack of SLR tracking data, which makes it difficult to obtain a consistently precise OD solution for HEO satellites. Nevertheless, because the signal of GNSS, which is conventionally used to track Earth-orbiting satellites, cannot easily reach HEO satellites due to its limited coverage, OD based solely on SLR should be useful for HEO satellites.
Given this critical situation, this research performed parametric studies for precise SLR-based OD of HEO satellites. Two HEO satellites were selected: Quasi-Zenith Satellite-1 (QZS-1), as an elliptical-inclined-geosynchronous-orbit (EIGSO) satellite, and Compass-G1, as a geostationary-orbit (GEO) satellite. Because the number of SLR tracking data has a significant influence on the precision of OD, this study selected the OD arc that maximizes the number of NPs. Also, two different methods of station bias estimation were implemented to analyze the associated effect on OD precision.
Section 2 of this paper describes the detailed information of each satellite and analyzes the SLR tracking data. For the OD of QZS-1, weight parameters of each SLR tracking station are adjusted by reflecting the quality of the measurements. Also, different settings of station bias estimation are set to enhance OD precision. As it is difficult to obtain a large amount of SLR tracking data for Compass-G1 on GEO compared with the case of QZS-1, the number of estimation parameters is reduced in the filtering process. The OD results of the two satellites in the given periods and their associated orbit overlap analyses are given in Section 3. Section 4 draws conclusions.
2 SLR-BASED ORBIT DETERMINATION
QZS-1 (Michibiki), the first satellite of the Japanese QZSS, was launched in September 2010 for technical validation of navigation satellites. Table 1 presents the mission parameters of QZS-1. The primary mission objective of its SLR is to calibrate the GPS-based orbit. Its orbit is set as EIGSO to maximize the satellite’s visibility from Japan. It has an eccentricity of 0.075 and an inclination of 45°, resulting in altitude change between 32,000 km and 40,000 km. Fig. 1 shows the ground tracks of QZS-1. The large inclination/eccentricity leads to an asymmetric figure-8shaped ground track.
Due to its local ground track, only those SLR tracking stations located in East Asia and Australia can obtain stable laser tracking data of QZS-1. QZS-1 can be successfully observed from seven SLR tracking stations: Beijing, Changchun, Koganei, Mount Stromlo, Shanghai, Tanegashima, and Yarragadee. Table 2 presents the detailed station information and tracking statistics. Among the seven stations, the Changchun and Yarragadee stations have contributed the main proportion of the SLR tracking data. Although Koganei contributed 15.04 % of the whole NPs, tracking procedures at this station have been suspended since March 11, 2014.
China has been establishing its own GNSS, called the Beidou navigation satellite system (BDS), in three phases of the development. The first stage of BDS, also known as the Beidou navigation satellite demonstration system (BDS-1), was established to implement the regional radio determination satellite service. The second stage (BDS- 2) initiated the first MEO satellite in 2007 and declared the beginning of the regional navigation satellite system (RNSS) in 2012 with 6 GEO, 5 inclined-geosynchronousorbit (IGSO), and 5 MEO satellites. The current BDS-2 satellites will be a part of the third stage of BDS (BDS-3) for constructing the GNSS by 2020 (Yang et al. 2017). The whole constellation of BDS-3 will consist of 27 MEO, 3 IGSO, and 5 GEO satellites. Currently, 3 MEO, 5 IGSO, and 1 GEO satellites are functioning with a laser retro-reflector array (LRA) payload.
Compass-G1, the first GEO satellite of BDS-2, was launched in January 2010 to provide positioning service for both military and civilian users in East Asia. Table 3 presents the mission parameters of Compass-G1. Due to its high altitude, its NP bin size is the same as that of QZS-1. The primary SLR application is precise OD. Note that the eccentricity and inclination are both near zero compared with those of QZS-1 to achieve GEO characteristics.
As Compass-G1 is GEO, fewer SLR tracking data are available. Table 4 summarizes the information of tracking stations. The Changchun station acquired most of the SLR tracking data, and the San Juan station and the Komsomolsk station rarely tracked Compass-G1. This was due to the relatively low elevation angle. As presented in Fig. 2, the ground track of Compass-G1 is fixed at a point, and the locations of the San Juan and Komsomolsk stations are far from the satellite.
In this study, GEODYN II, developed by NASA GSFC, was used to obtain the OD solution (Pavlis et al. 1998). The GEODYN II consists of an orbital dynamics model, a measurement model, and an estimation filter based on batch least-square. Table 5 shows the associated parameter settings of the OD. This study adopted a stations’ coordinate system, updated in 2013, based on the SLRF2005 coordinate system. The equations of motion of satellite contain central gravity and a variety of perturbations (Tapley et al. 2004):(1)
| Model/parameter | Description | References |
|---|---|---|
| Earth gravity | GGM02C 30×30 | Tapley et al. 2005 |
| Third body gravity | Moon, Sun, and all planets | |
| Planetary ephemeris | JPL DE-403 | Standish et al. 1995 |
| Atmospheric model | Jacchia 1971 | Jacchia 1971 |
| SLR station coordinates | ITRF2005 | Altamimi et al. 2007 |
| Solar radiation pressure | CR coefficient = 1.13 | |
| Numerical integration | Cowell’s 11th method Step size = 300 sec |
Here, contains the effects of the non-spherical gravity of the Earth, the gravity of the celestial bodies in the solar system, solar radiation pressure, and atmospheric perturbations. For celestial bodies, the Moon, the Sun, and all planets are included from the JPL DE-403 planetary ephemeris information. The attitude model of the satellites is set as the cannonball model, because their specific attitude profiles are unknown.
The measurement model of SLR consists of the geometric relationship defined by observation, measurement bias, and timing bias of the tracking stations (Pavlis et al. 1998):(2)
Here, denotes the computed observation at time is the geometric relationship defined by the Earth-fixed position vector of the satellite , the velocity vector , and the Earth-fixed position vector of the station , b is a constant bias on the measurement, and Δt is the timing bias associated with the measurement.
To observe QZS-1 and obtain a sufficient number of NPs, JAXA conducted a tracking campaign from February 25 to March 7, 2013 (Kasho et al. 2013). To take full advantage of the observed data during this campaign period, this study set the OD arc of QZS-1 to be the same period. During this time span, 105 NPs were freely distributed online by ILRS, and 269 unpublished NPs were also available courtesy of JAXA (Table 6). This period was divided into two singleweek arcs with overlap, March 1 to March 7 and March 2 to March 8, to perform the orbit overlap for internal quality assessment. Due to the relatively small amount of tracking data, all the NPs obtained from March 1 to March 8, 2013 were used for OD.
Unlike QZS-1, the whole NPs for Compass-G1 are accessible online for selected OD arcs. Therefore, the optimal OD arc that maximizes the number of NPs was searched from the whole tracked period from year 2012 to 2017. After the comparison, the OD arc from January 1 to January 10, 2016, was selected for Compass-G1. Similarly, in the case of QZS-1, this period was divided into two arcs with overlap: January 1 to January 7 and January 4 to January 10. Table 7 presents the number of NPs in this arc. Despite successful observations of Compass-G1 by eight stations during the entire tracking period, as shown in Table 4, only the Changchun and Yarragadee stations tracked Compass-G1 in this period. The Changchun station obtained most of the NPs, but the Yarragadee station obtained three NPs.
| Date | Station Number | No. NPs |
|---|---|---|
| 1/1 | 7237 | 4 |
| 1/2 | 7237 | 9 |
| 1/3 | 7237 | 7 |
| 1/4 | - | - |
| 1/5 | 7237 | 11 |
| 1/6 | 7237 | 6 |
| 1/7 | 7237 | 12 |
| 1/8 | 7090, 7237 | 21 |
| 1/9 | - | - |
| 1/10 | - | - |
| Total | 7090, 7237 | 68 |
In this study, the orbit overlap method was utilized to internally assess the OD quality of QZS-1 and Compass-G1 because their true (exact) orbit is unknown. The orbit overlap method is one of the quantitative indicators of estimated orbit precision (Tapley et al. 2004). Fig. 3 shows the concept of the orbit overlap for QZS-1 and Compass-G1, respectively. The OD of each arc was performed separately, and the OD results were compared with each other for the overlap period. In this study, the overlap orbits were directly compared with each other every 5 minutes. For the whole eight-day period of QZS-1, two single-week OD arcs were selected, and there were six overlap days. Similarly, Compass-G1 had four overlap days: January 4 to January 7, 2016.
3 ORBIT DETERMINATION RESULTS
GEODYN II possesses two kinds of station timing bias estimation settings. The MBIAS setting estimates the biases once in an OD period, whereas the PBIAS setting determines them at every pass (Pavlis et al. 2006). The expected OD precision is higher when using PBIAS than when using MBIAS because the timing biases may change for each pass. However, when only published NPs are used, the OD of QZS-1 using the PBIAS setting fails because of an insufficient number of NPs. When unpublished NPs are added, the OD can be successfully achieved using PBIAS. Also, the weighting sigma of each station should be adjusted differently to improve the performance of the OD results. The ILRS Analysis Centers (ACs) publishes monthly/quarterly performance reports of tracking stations. The ACs estimate SLR tracking quality by obtaining the NP RMS of the LAGEOS-1 satellite. Five ACs issued performance reports in March 2013, and this study followed the results of the Mission Control Center (MCC) AC because the MCC is the only AC to distribute tracking performance results for the Koganei station. Regarding the analysis reports, among the QZS-1 tracking stations, the Yarragadee station obtained the best SLR tracking quality, whereas the Shanghai/Beijing/Koganei stations provide relatively degraded data during this period. These results were applied to the sigma weighting strategy for QZS-1 OD to set the weight parameters for the Yarragadee and Shanghai/ Beijing/Koganei stations as 1 and 10, respectively.
Table 8 presents the post-fit observation-calculatedobservation (O-C) residual of QZS-1 for the two arcs with the MBIAS setting. The post-fit residual for arc 1 (March 1– March 7, 2013) with 368 NPs is 11.98 cm, and that for arc 2 (March 2–March 8, 2013) with 347 NPs is 10.77 cm. Three and 11 NPs were rejected from arc 1 and arc 2, respectively, for the OD based on the MBIAS setting. The average residual between the two arcs is 11.375 cm. Changchun station’s NPs were rejected for the OD of arc 2 with the MBIAS setting. The OD results of the two arcs were directly compared with each other by overlap. Fig. 4 and Table 9 show the position differences for the six overlap days. Fig. 4 presents the overlap error in the Earth-centered radial-tangentialnormal (RTN) coordinate system and the 3-dimensional overlap errors for the whole period. The overlap differences in RTN coordinates are 6.839 m, 52.029 m, and 21.053 m, and the mean RMS error with the MBIAS setting is 55.013 m.
| Overlap Period | Radial Error (RMS) | Along-Track Error (RMS) | Cross-Track Error (RMS) | Mean RMS Error |
|---|---|---|---|---|
| 3/2/2013~3/7/2013 | 4.839 m | 52.029 m | 21.053 m | 55.013 m |
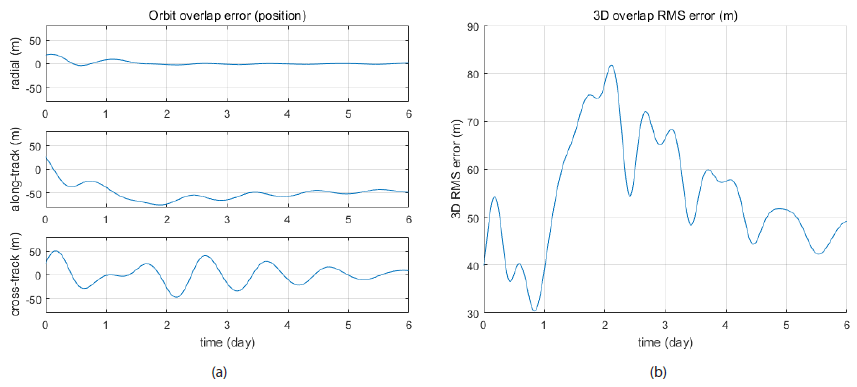
Table 10 shows the QZS-1 OD results of the two arcs with the PBIAS setting. The post-fit O-C residual for arc 1 with 371 NPs is 3.60 cm, and that for arc 2 with 358 NPs is 2.40 cm. The average residual of the two arcs is 3 cm. The O-C residuals of two arcs’ OD decrease when station biases are estimated more frequently. As the SLR residual of the QZS-1 satellite presented in Akiyama & Otsubo (2012) was 17.9 cm on average for three different 5-7 day-long arcs, the residual obtained from this study is acceptable. Fig. 5 and Table 11 show the position differences for the six overlap days with the PBIAS setting. The overlap errors decreased significantly with the PBIAS setting, which yielded 0.214 m, 1.004 m, and 1.672 m in the RTN coordinate system. The mean RMS error with PBIAS is 1.962 m, which is 28 times smaller than that with MBIAS; it is effective for enhancing the precision of OD to estimate the station bias at every pass.
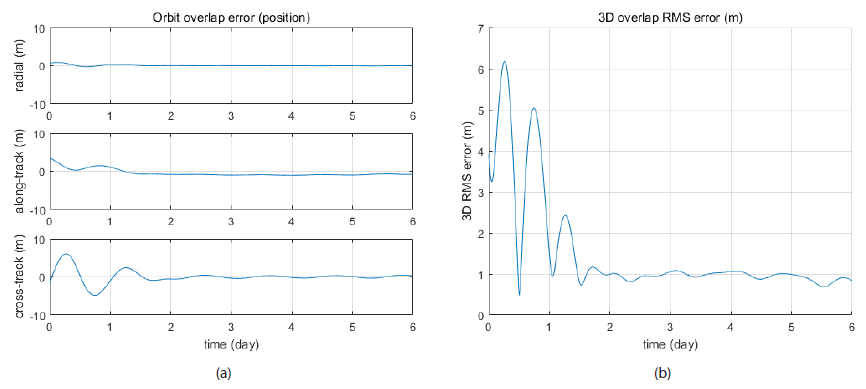
| Overlap Period | Radial Error (RMS) | Along-Track Error (RMS) | Cross-Track Error (RMS) | Mean RMS Error |
|---|---|---|---|---|
| 3/2/2013~3/7/2013 | 0.214 m | 1.004 m | 1.672 m | 1.962 m |
Given that only 68 NPs are available, the PBIAS setting is not applicable to OD for Compass-G1, unlike the case of OD for QZS-1. The total number of estimation parameters for the OD of Compass-G1 reaches 122 with the PBIAS setting, whereas it is only 22 with the MBIAS setting. Furthermore, the sigma weighting strategy is also unavailable because only one station, Changchun, provides most of the NPs for Compass-G1, and the Yarragadee station provides the minimal number of NPs. As the NPs from the Yarragadee station were obtained on January 8, they could be used for only the second arc (January 4 to January 10). If these NPs were included in the OD of Compass-G1, the OD precision would be degraded. Therefore, these NPs were removed in the OD process for consistency.
The Compass-G1 OD results with consideration of the above NP issue are presented in Table 12. The post-fit O-C residual for arc 1 (January 1 to January 7, 2016) with 49 NPs is 8.81 cm, and that for arc 2 (January 4 to January 10, 2016) with 47 NPs is 12.00 cm. The corresponding OD precision is lower compared with that of QZS-1, as the number of NPs is lower. This reduction in precision is clearly seen in the orbit overlap results. Fig. 6 and Table 13 show that the errors are 18.957 m, 75.651 m, and 160.476 m in RTN coordinates for the four-day overlap period. Also, the 3-dimensional mean overlap error reaches 160.564 m. These results indicate that a reduction in estimation parameters such as timing biases induces a significant increase in orbit overlap error, even with a quite precise O-C residual.
| Station | Station Number | No. NPs (arc 1) | O-C Residual (arc 1) | No. NPs (arc 2) | O-C Residual (arc 2) |
|---|---|---|---|---|---|
| Changchun | 7237 | 49 | 8.81 cm | 47 | 12.00 cm |
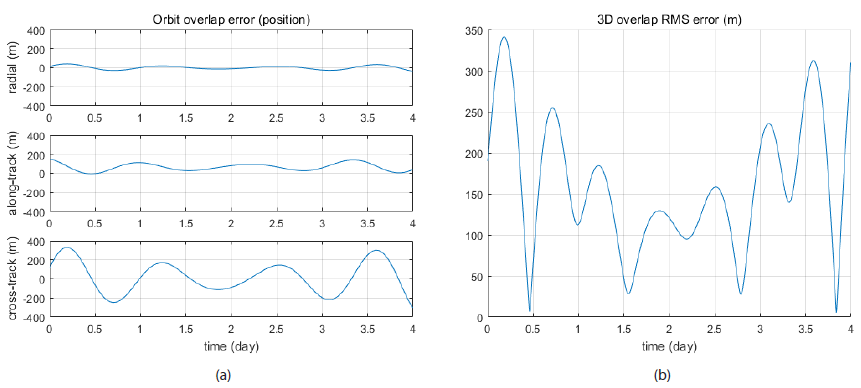
| Overlap Period | Radial Error (RMS) | Along-Track Error (RMS) | Cross-Track Error (RMS) | Mean RMS Error |
|---|---|---|---|---|
| 1/4/2016~1/7/2016 | 18.957 m | 75.561 m | 160.475 m | 160.564 m |
4 CONCLUSIONS
OD was performed on HEO satellites using sparse SLR measurements. Two satellites, QZS-1, with an ellipticalinclined- geosynchronous orbit, and Compass-G1, with a geostationary orbit (GEO), were selected. NASA GSFC GEODYN II software was utilized to perform the OD using NP SLR observations. The periods of OD arcs were selected carefully to maximize the number of NPs. While performing the OD for week-long arcs, the overlap days of two arcs were directly compared to obtain orbit overlap results for efficient internal quality assessment of estimated orbit. For QZS-1, both MBIAS and PBIAS were selected to estimate the SLR tracking stations’ timing biases, and the sigma weighting strategy was applied to give different weights according to the tracking performance of stations. The resultant post-fit position residuals of QZS-1 were 11.375 cm and 3 cm on average for two arcs with the MBIAS and PBIAS setting, respectively, and the resultant 3-dimensional mean overlap error decreased from 55.013 m (MBIAS) to 1.691 m (PBIAS). For Compass-G1, because the Changchun station was the only station capable of producing NPs, the number of NPs was quite low compared with the case of QZS-1. Therefore, only the MBIAS setting was applied to the OD of Compass-G1, and the sigma weighting strategy for tracking stations was not applied. The result yielded a mean O-C residual of 10.405 cm and an average overlap error of 160.564 m. The significantly large orbit error of Compass-G1 implies that estimating the pass-by-pass bias and applying the sigma weighting strategy with enough NPs from different tracking stations is critical for enhancing the precision of OD. The OD results of Compass-G1 also indicate that there must be a reduction in other estimation parameters such as solar radiation pressure or general acceleration to estimate the pass-by-pass bias with a small amount of data. As more frequent estimation of station bias makes improves OD quality, a trade-off study considering the selection of the PBIAS setting and other estimation parameters will be necessary to improve OD precision. Also, progressing a satellite-tracking campaign by several stations can be an alternative to increasing the number of NPs in a short period and therefore to improving OD precision. The OD strategy presented in this study is applicable to continuous orbit monitoring of HEO satellites.


